 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Bob weighs himself on his bathroom scale. The smallest divisions on the scale are 1-pound marks, so the least count of the instrument is 1 pound.
Bob reads his weight as closest to the 142-pound mark. He knows his weight must be larger than 141.5 pounds (or else it would be closer to the 141-pound mark), but smaller than 142.5 pounds (or else it would be closer to the 143-pound mark). So Bob's weight must be
weight = 142 +/- 0.5 pounds
In general, the uncertainty in a single measurement
from a single instrument is
half the least count of the instrument.
What is the fractional uncertainty in Bob's weight?
uncertainty in weight
fractional uncertainty = ------------------------
value for weight
0.5 pounds
= ------------- = 0.0035
142 pounds
What is the uncertainty in Bob's weight, expressed as a percentage of his weight?
uncertainty in weight
percentage uncertainty = ----------------------- * 100%
value for weight
0.5 pounds
= ------------ * 100% = 0.35%
142 pounds
When one combines several measurements together, one can often determine the fractional (or percentage) uncertainty in the final result simply by combining the uncertainties in the several quantities.
Jane needs to calculate the volume of her pool, so that she knows how much water she'll need to fill it. She measures the length, width, and height:
length L = 5.56 +/- 0.14 meters
= 5.56 m +/- 2.5%
width W = 3.12 +/- 0.08 meters
= 3.12 m +/- 2.6%
depth D = 2.94 +/- 0.11 meters
= 2.94 m +/- 3.7%
To calculate the volume, she multiplies together the length, width and depth:
volume = L * W * D = (5.56 m) * (3.12 m) * (2.94 m)
= 51.00 m^3
In this situation, since each measurement enters the calculation as a multiple to the first power (not squared or cubed), one can find the percentage uncertainty in the result by adding together the percentage uncertainties in each individual measurement:
percentage uncertainty in volume = (percentage uncertainty in L) +
(percentage uncertainty in W) +
(percentage uncertainty in D)
= 2.5 % + 3.7%
= 8.8%
Therefore, the uncertainty in the volume (expressed in cubic meters, rather than a percentage) is
uncertainty in volume = (volume) * (percentage uncertainty in volume)
= (55.00 m^3) * (8.8%)
= 4.84 m^3
Therefore,
volume = 55.00 +/- 4.84 m^3
= 55.00 m +/- 8.8%
Jane's measurements of her pool's volume yield the result
volume = 55.00 +/- 4.84 m^3
When she asks her neighbor to guess the volume, he replies
"52 cubic meters."
Are the two estimates consistent with each other?
In order for two values to be consistent within the uncertainties, one should lie within the range of the other. Jane's measurements yield a range
55.00 - 4.83 m^3 < volume < 55.00 + 4.83 m^3
50.17 m^3 < volume < 59.83 m^3
The neighbor's value of 52 cubic meters lies within this range, so Jane's estimate and her neighbor's are consistent within the estimated uncertainty.
Joe is making banana cream pie. The recipe calls for exactly 16 ounces of mashed banana. Joe mashes three bananas, then puts the bowl of pulp onto a scale. After subtracting the weight of the bowl, he finds a value of 15.5 ounces.
Not satisified with this answer, he makes several more measurements, removing the bowl from the scale and replacing it between each measurement. Strangely enough, the values he reads from the scale are slightly different each time:
15.5, 16.4, 16.1, 15.9, 16.6 ounces
Joe can calculate the average weight of the bananas:
15.5 + 16.4 + 16.1 + 15.9 + 16.6 ounces
average = -------------------------------------------
5
= 80.4 ounces / 5 = 16.08 ounces
Now, Joe wants to know just how flaky his scale is. There are two ways he can describe the scatter in his measurements.
0.5 + 0.4 + 0.1 + 0.1 + 0.6 ounces
mean dev from mean = --------------------------------------
5
= 1.6 ounces / 5 = 0.32 ounces
[ (0.5)^2 + (0.4)^2 + (0.1)^2 + (0.1)^2 + 0.6)^2 ]
stdev from mean = sqrt [ ----------------------------------------------- ]
[ 5 - 1 ]
[ 0.79 ounces^2 ]
= sqrt [ -------------- ]
[ 4 ]
= 0.44 ounces
Either the mean deviation from the mean, or the standard deviation from the mean, gives a reasonable description of the scatter of data around its mean value.
Can Joe use his mashed banana to make the pie? Well, based on his measurements, he estimates that the true weight of his bowlful is (using mean deviation from the mean)
16.08 - 0.32 ounces < true weight < 16.08 + 0.32 ounces
15.76 ounces < true weight < 16.40 ounces
The recipe's requirement of 16.0 ounces falls within this
range, so Joe is justified in using his bowlful to make the recipe.
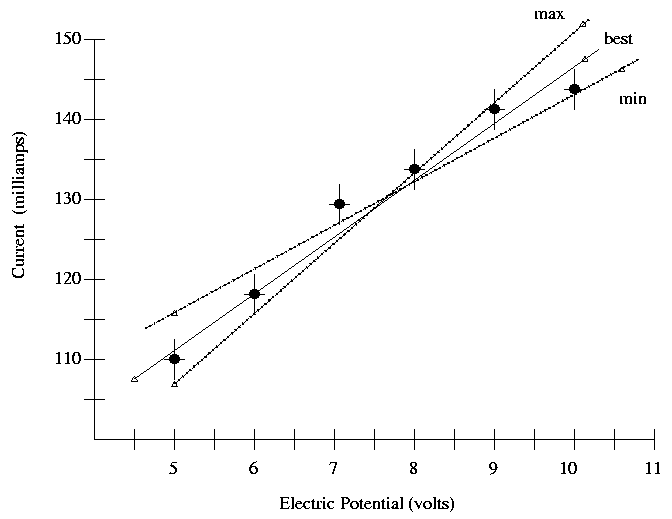
If one has more than a few points on a graph, one should calculate the uncertainty in the slope as follows. In the picture below, the data points are shown by small, filled, black circles; each datum has error bars to indicate the uncertainty in each measurement. It appears that current is measured to +/- 2.5 milliamps, and voltage to about +/- 0.1 volts. The hollow triangles represent points used to calculate slopes. Notice how I picked points near the ends of the lines to calculate the slopes!

In the example above, I find
147 mA - 107 mA mA
"best" slope = ------------------ = 7.27 ----
10 V - 4.5 V V
145 mA - 115 mA mA
"min" slope = ------------------ = 5.45 ----
10.5 V - 5.0 V V
152 mA - 106 mA mA
"max" slope = ------------------ = 9.20 ----
10 V - 5.0 V V
mA
Uncertainty in slope is 0.5 * (9.20 - 5.45) = 1.875 ----
V
There are at most two significant digits in the slope, based on the uncertainty. So, I would say the graph shows
mA
slope = 7.3 +/- 1.9 ----
V
Last modified 10/11/2000 by MWR.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.