Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
When Galileo turned his telescope to the skies in 1610, he noticed that Jupiter was not alone. As the planet drifted through the sky, it was accompanied by four smaller dots of light. From one night to the next, these smaller dots changed their relative positions around the planet.
Image courtesy of
Science Photo Library
Galileo quickly realized that these four objects were moons which circled around Jupiter. By observing them over many months, he and other astronomers were able to determine the periods of all four of these "Galilean satellites" to high precision.
That precision allowed scientists to predict when various events would occur. For example, they could predict the time when one of the moons would pass behind the edge of the planet, as seen from Earth. Click on the image below to start a brief animation.
Roughly sixty years later, some observers noticed a problem: while the predicted events in the Jovian system did happen at roughly the right time, there were discrepancies; sometimes events were ahead of the predicted time, and other times the events fell behind. The differences weren't tiny: they could be as large as about 11 minutes before or after the ephemeris. These differences weren't random, but appeared to come in groups: for a while, all the events would occur too soon, then the predictions would be correct, and then they all would start falling behind for a while.
Q: What was causing these discrepancies between the
predicted and observed times?
The answer is ... the speed of light!
At some times -- for example, in July, 1676 -- the Earth was on the same side of the Sun as Jupiter. In this situation, the light rays from Jupiter and its moons would reach the Earth a little earlier than usual, and so Roemer and other astronomers would record the events as happening a bit earlier than predicted.
But at other times -- for example, in January, 1677 -- the Earth was on the far side of the Sun, away from Jupiter. Since the light rays would take extra time to traverse (nearly) the diameter of Earth's orbit, eclipses of the Galilean moons would fall behind schedule.
Roemer was the first to realize that one could turn this lemon into lemonade: using the size of these variations in eclipse times, and the best estimates for the size of the Earth's orbit, he was able to make the first decent measurement of the speed of light.
Give it a try, but use a modern value for the diameter of the Earth's orbit to make it easier. That means the value you compute below won't match exactly the value that Roemer found, because his knowledge of the Earth's orbital size wasn't quite so good.
Q: What is the change in distance that light rays from
Jupiter must travel to reach the Earth?
That is, the difference between maximum and averge,
or between average and minimum. Express your answer in kilometers.
Q: Assume that the amplitude of these variations in time
is about eleven minutes. Calculate the speed of light.
Not bad, Mr. Roemer!
Now, what does all of this have to do with "astronomical systems of time?" That point is that exactly the same phenomenon -- a shift of events to earlier or later times, depending on the location of the Earth in its orbit around the Sun -- will occur when we look at STARS, as well as the moons of Jupiter. In other words, unless we are careful, we will find systematic errors in our predictions for, say, the time when a variable star will reach its maximum light.
Q: Is there any way to avoid these variations in event time?
One way to avoid errors in the prediction, or observation, of the times of some celestial event is to account for the relative positions of the Earth and the object being observed, and correct for the distance above, or below, the average between Earth and target.
When does the distance have its average value? Well, it's when the Earth and the target object make an angle of 90 degrees, as seen from the Sun.
If the Earth happens to be in that special location, then we don't need to make any corrections. But if Earth is somewhere else along its orbit, we need to determine how much farther, or less far, light from the target must travel to reach the Earth than it would need to reach the average position. We can then add a correction to the predicted time of the event.
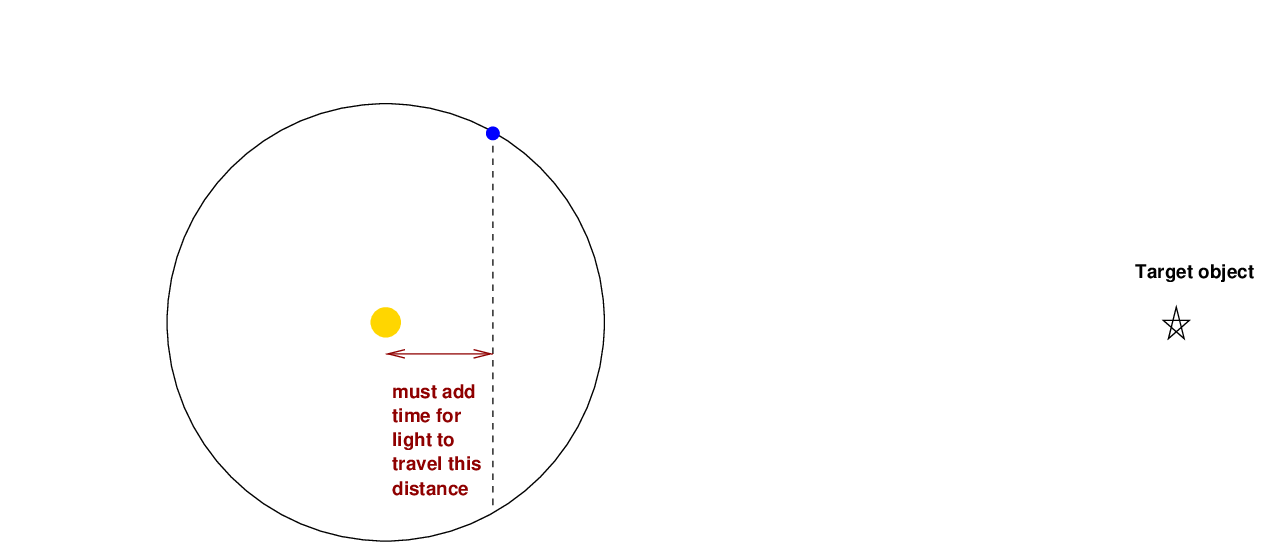
This is exactly equivalent to determining when an observer sitting on the Sun would see the event.
When discussing events which occur over long time scales of months or years, astronomers often perform all their calculations as if they were made for a heliocentric observer: one who sits on the Sun. In that way, they avoid having to account for the effects of time travelling across Earth's orbit.
In particular, a version of Julian Date which has been corrected for this effect is known as Heliocentric Julian Date, or HJD for short. In order to compute HJD, one must know
The big advantage of HJD is that it allows us to compute the time of future celestial events very simply, without having to worry about where the Earth will be in its orbit.
So, how can one actually calculate the HJD for a particular observation? Here are some sites that will do the job:
Let's practice using HJD. Just to make things easy, let's pretend we could make measurements right now, in the middle of class (even though it's daytime in Rochester). Adopt the following time for all of the following exercises:
time of observation = EST 2024 Jan 31 02:30 PM
Answer all the following questions:
Now, consider two different variable stars. One of them is almost in the same direction as the Sun, while the other is nearly opposite to the Sun in the sky. For each one, fill in the following table: compute the HJD of an observation made at 2:30 PM today, and the difference between the HJD of that measurement and the current JD.
Name RA Dec HJD delta (HJD - JD)
--------------------------------------------------------------------
S Cap
X Cnc
--------------------------------------------------------------------
Here's an optional bonus question you can hand it later.
BONUS! Can you find a variable star for which an observation
at this time yields an HJD which is almost
exactly the same as the JD? The difference
between them must be no more than 0.001 days.
See the extra-credit project for rules and details.
The Earth moves in its orbit around the Sun, so at some times it will be closer to a particular star, and at other times, it will be farther away. That will lead to variations in the time at which we observe events on that star which can be at most
radius of Earth's orbit
maximum size of HJD corrections = ------------------------
speed of light
1.5 x 1011 m
= ---------------------
3 x 108 m/s
= 500 s = 8.3 minutes
By calculating the Heliocentric Julian Date, we compute the time at which those events on a distant star would be recorded by an observer on the Sun. And, since the Sun sits motionless at the center of the Solar System, there won't be any variations caused by the Sun's motion.
Right?
WRONG!
It turns out that the Sun does NOT sit motionless at the center of the Solar System. It is subject to the gravitational forces of all the planets and asteroids and comets and other material; and, since all those objects are moving, the combination of their gravitational forces changes size and direction. As a result, the Sun accelerates and moves in a rough little orbit of its own around the barycenter (center of mass) of the Solar System.
Click on the picture below to see its motion.
The diagram below shows the orbital path of the Sun around the barycenter. Note that at this moment, May 2071, the start of our little animation, the Sun was roughly at the right-hand side of its orbit.
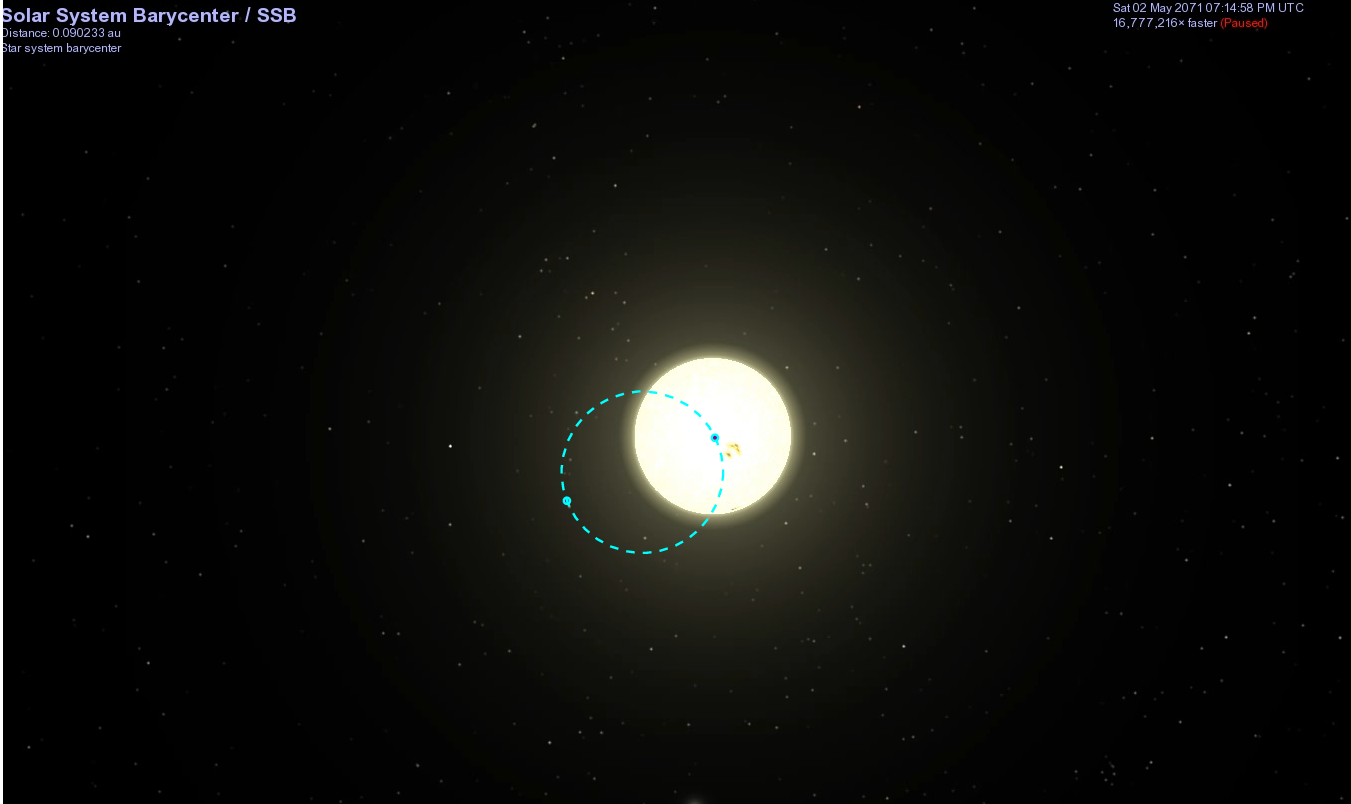
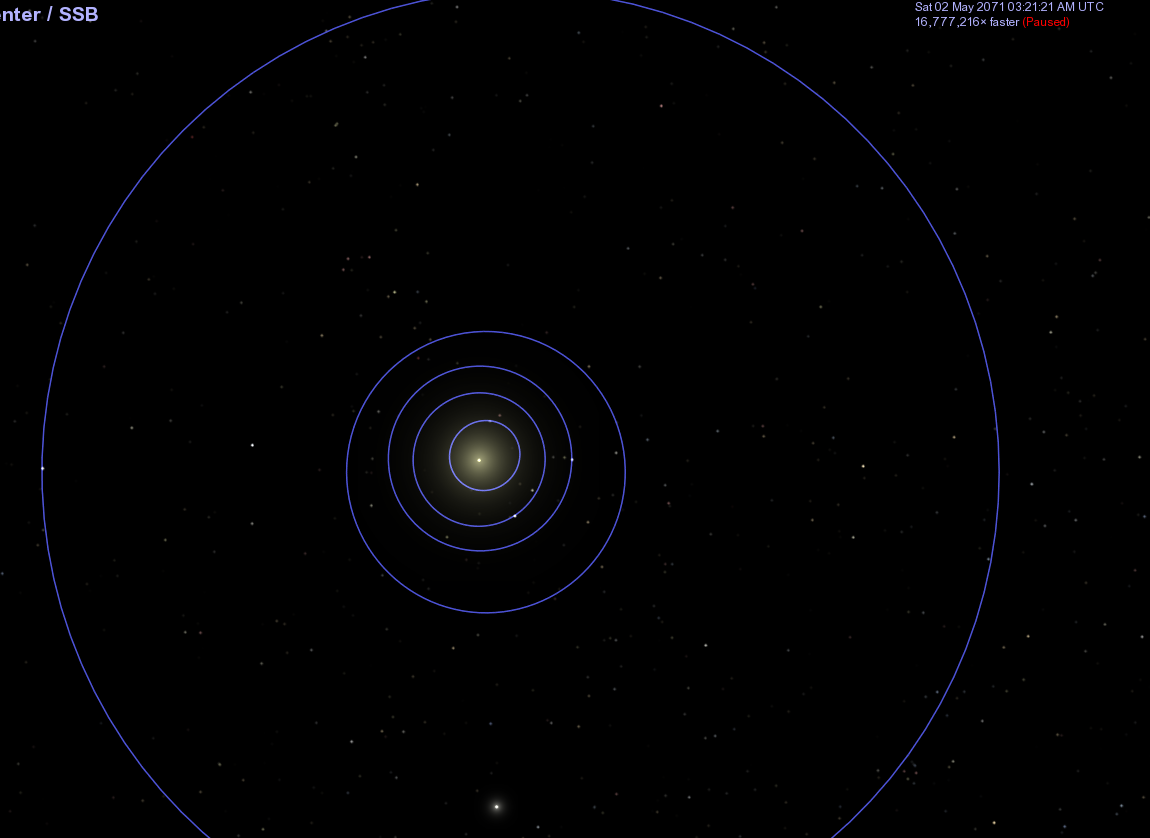
Let's zoom out to take a look at the positions of other objects at this time. In particular, where is Jupiter?
About 6.5 years later, the Sun reaches the other side of its little orbit:
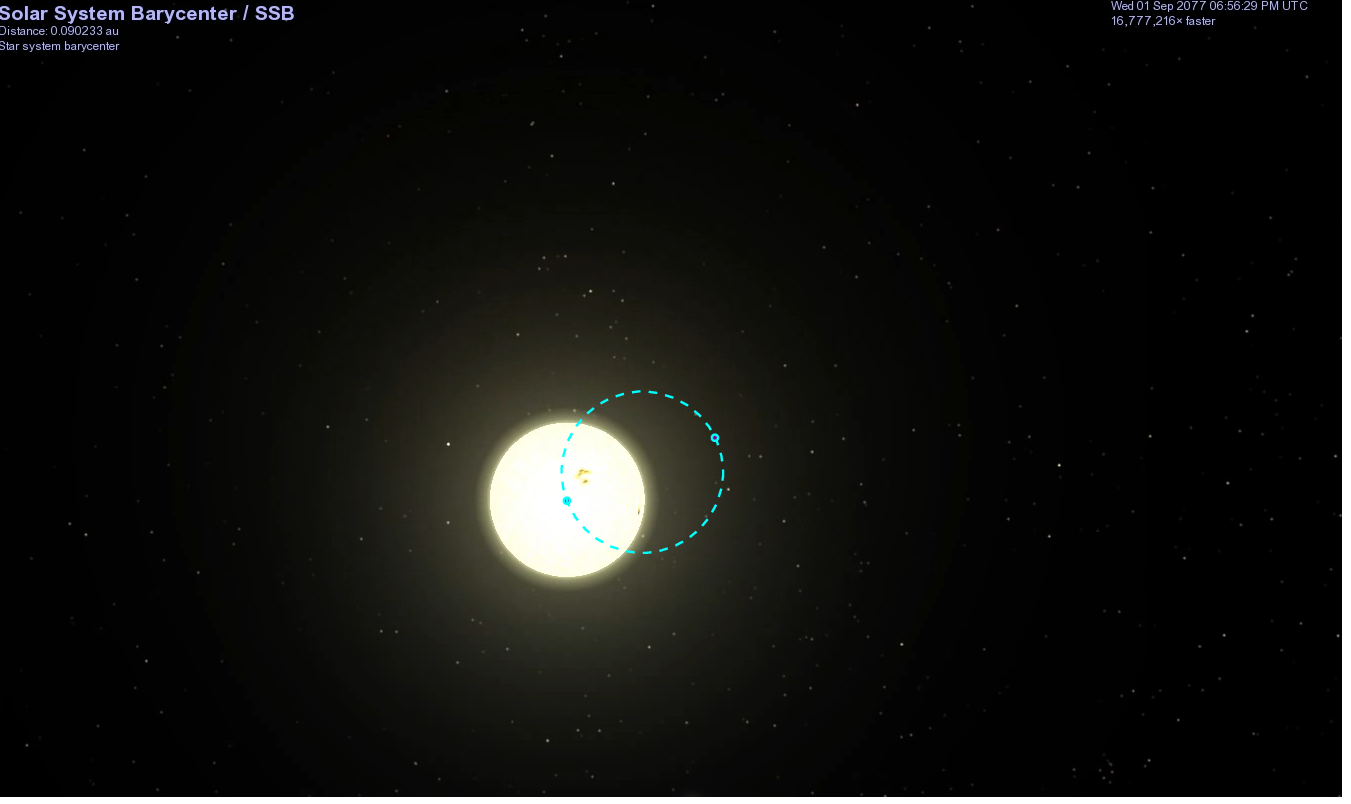
Again, look at the wide view. Where is Jupiter now?
It turns out that because Jupiter is so much more massive than all the other planets, and because it is closer to the Sun than the other gas giants, its gravitational force on the Sun dominates all others. To a good approximation, the Sun orbits around its center of mass with Jupiter.
What's the size of the correction we need to make for this motion of the Sun? Well, because the Sun moves in such a tiny little orbit, the difference in time it creates for objects in different directions is a tiny little offset. Just how long does it take for a beam of light to travel across the Sun's orbit? Well, take a look:
The radius of the Sun's motion around the solar system barycenter is just about equal to the radius of the Sun itself.
Q: What is the radius of the Sun, in meters?
Q: How long will it take a beam of light to travel that distance?
Express your answer in seconds and in days.
For most purposes, the regular old HJD is good enough. But astronomers who study objects which change in very short timescales, such as pulsars and gamma-ray bursts, need to convert all their measurements into BJD.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.