Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Recall that there are several different types of noise which occur in CCD images:
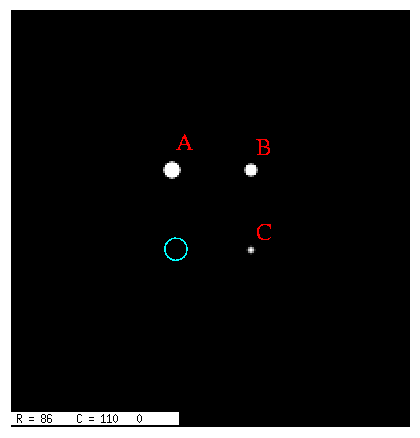
Let's consider several typical situations that arise in astronomical observations. We'll focus on a field of artificial stars, each with FWHM of 3 pixels:
For simplicity, the simulations have a gain of 1 electron per count. We'll use an aperture of radius 5 pixels, indicated by the circle in the figure above, to measure the light from each star There are pi*5*5 = 79 pixels inside the aperture.
Suppose that the sky is very dark and the CCD's amplifier is nearly perfect; then light from the stars is the dominant source of both signal and noise. Even the faint star "C" shows up perfectly above its surroundings:
electrons electrons electrons
Star from star from sky from readnoise
perpix total perpix total
------------------------------------------------------------------
A 80,800 0 0 0 0
B 8,080 0 0 0 0
C 808 0 0 0 0
------------------------------------------------------------------
Astronomers call images like this shot-noise limited.
The S/N ratio for each star is simply the signal from the star over the noise from the star. For star C, for example,
signal 808 808
S/N = --------------- = ----------- = ------- = 28
noise sqrt(808) 28
If we double the exposure time, what happens to the S/N ratio?
2*808 2 808
S/N = -------------- = ------ * ----------- = sqrt(2) * 28
sqrt(2*808) sqrt(2) sqrt(808)
The S/N ratio in this regime increases as the square root of the exposure time. To double the S/N ratio, one must increase exposure time by a factor of four.
Now, let's increase the sky background from zero to a moderate value: 64 counts per pixel. An image of the field now shows mottling of the background, due to random fluctuations in the sky level from pixel to pixel.
electrons electrons electrons
Star from star from sky from readnoise
perpix total perpix total
------------------------------------------------------------------
A 80,800 64 5056 0 0
B 8,080 64 5056 0 0
C 808 64 5056 0 0
------------------------------------------------------------------
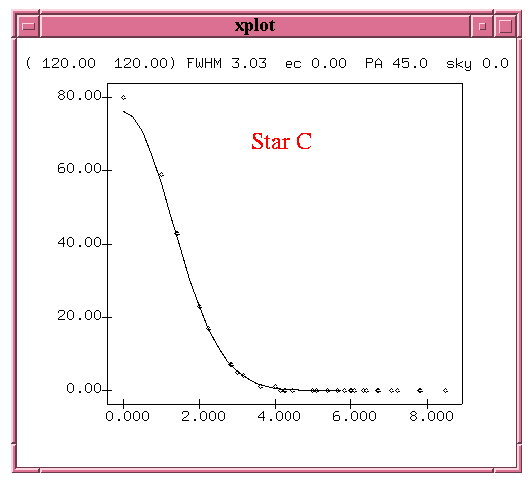
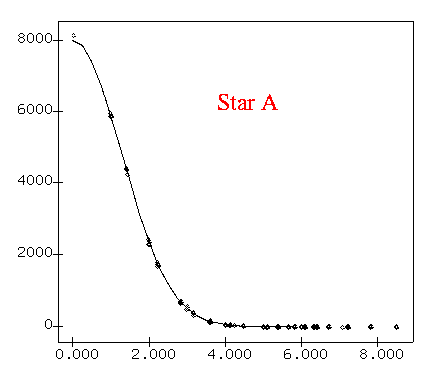
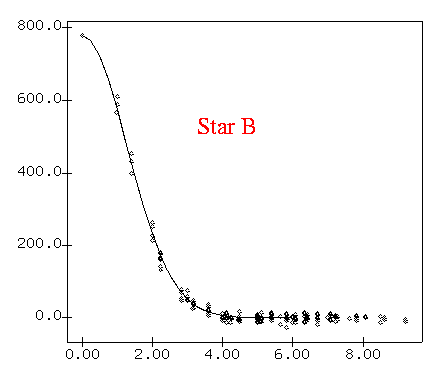
Radial profiles of the fainter stars show this noise in the background.
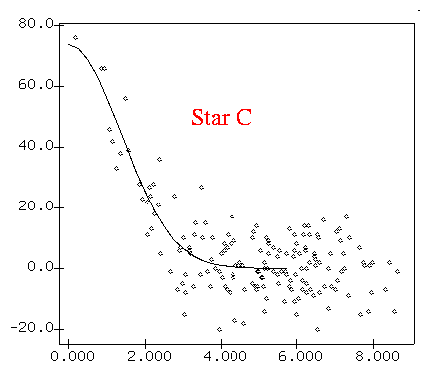
What if the sky is very bright compared to one's target object? That is, what if the sky background contributes many more electrons to a pixel than the star? Let's increase the average sky level in the simulation to 800 electrons.
electrons electrons electrons
Star from star from sky from readnoise
perpix total perpix total
------------------------------------------------------------------
A 80,800 800 63,200 0 0
B 8,080 800 63,200 0 0
C 808 800 63,200 0 0
------------------------------------------------------------------
Radial profiles show the background now swamping the faint star "C".
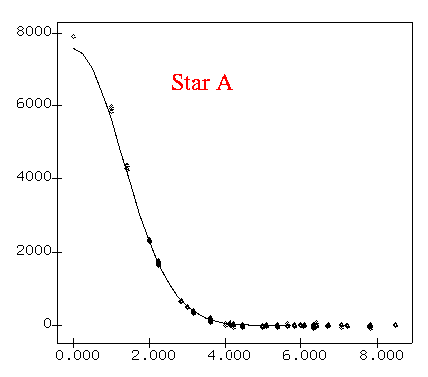
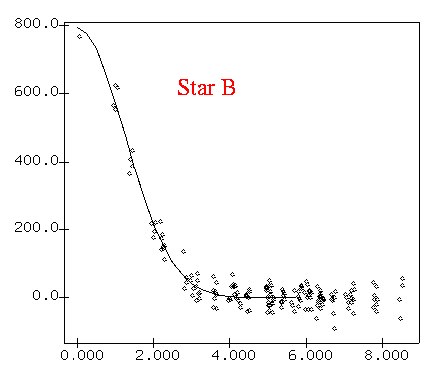
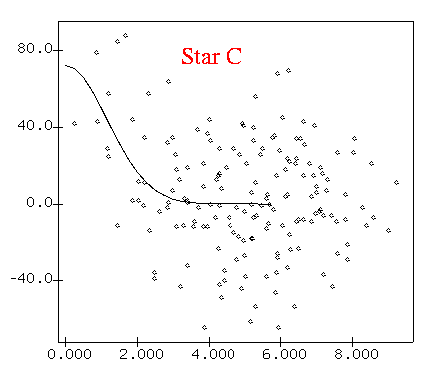
When the number of electrons contributed by the background sky inside the aperture is much larger than that contributed by the target star -- the background-limited regime -- how does the S/N ratio change with exposure time?
Again, look at star C. The mean background level is 800 counts = 800 electrons.
signal 808 808
S/N = --------------- = --------------------- = ------- = 3.2
noise sqrt( 808 + 79*800 ) 251
If we double the exposure time, what happens to the S/N ratio?
2*808 808
S/N = ---------------------- = sqrt(2) * -------------------
sqrt(2*808 + 79*2*800) sqrt( 808 + 79*800)
= sqrt(2) * 3.2
Hmmmm. Once again, the S/N ratio rises with the square root
of the exposure time ... just as for the shot-noise-limited regime.
The last regime typically occurs if one takes very short exposures of a faint source with a cheap CCD. The dominant source of noise may be the readout noise of the amplifier. The important thing here is that this readout noise does not depend on the length of the exposure.
Suppose that we look at star "C" with a 1-second exposure: the sky background is negligible, but the readout noise is 100 electrons.
signal 808
S/N = --------------- = ------------------------- = 0.91
noise sqrt( 808 + 79*(100*100) )
electrons electrons electrons
Star from star from sky from readnoise
perpix total perpix total
------------------------------------------------------------------
A 80,800 0 0 10,000 790,000
B 8,080 0 0 10,000 790,000
C 808 0 0 10,000 790,000
------------------------------------------------------------------
Now, if we double the exposure time, we get more electrons from the star, but the same number from the amplifier:
2*808
S/N = -------------------------- = 1.82
sqrt(2*808 + 79*(100*100))
= 2 * 0.91
Now, in this case, the S/N ratio does increase (nearly)
linearly with exposure time.
However, as soon as the signal from the star becomes
comparable to the electrons contributed by readout noise,
this happy situation comes to an end.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.