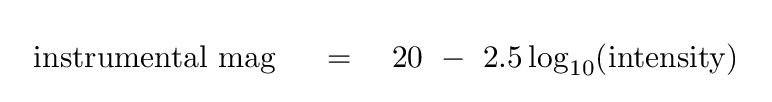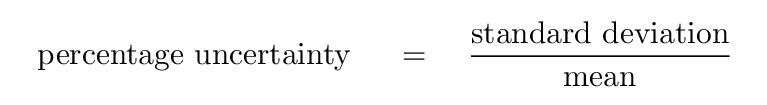Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Magnitudes, light curves, and uncertainty
Today's lab exercise should be carried out in pairs,
ideally, but it's okay to do it by yourself
or in a group of three.
In order to gain credit for this exercise,
you must create a PDF document
which provides the answers to all the questions
and items written in red.
Submit the PDF to the instructor via the
"Assignments" tab in myCourses.
In order to carry out the tasks in this exercise,
you will need several tools:
- a tool to compute mean and standard deviation of a set of numbers
- a tool to create simple X-Y scatter graphs from a datafile
You may use a spreadsheet of some sort,
or you may try one of a large number of programs
designed for the analysis of datasets.
Some students can make very nice plots using Python and
matplotlib.
I prefer to use this tool:
You will eventually use our telescopes and cameras to take a
set of images of your target star on one or two nights.
There will be LOT of images -- maybe 100 to 400.
You'll use a program called
AstroImageJ
to display and process these images,
and then to measure the brightness of stars in those images.
At the end of the work,
you'll have a big datafile with many, many columns of
numbers.
Today, we'll practice on a much simpler dataset.
The files you will use as input for your work
are plain ASCII text files with a format like this:
# measurements of the intensity of three stars
# JulianDay A B C
#
2459610.00000 1011.01 835.21 166.78
2459610.00139 997.21 861.85 150.97
2459610.00278 1005.10 855.06 174.02
2459610.00417 995.70 858.74 162.25
There are four columns:
the first records the time when the image was taken,
in the form of a
Julian Date.
The good news is that using Julian Dates to keep track of time
makes many calculations convenient --
the number just increases by 1 for every day that passes.
We don't have to remember how many days are in September,
or how to handle leap years.
The bad news is that Julian Day values are large numbers,
so they can sometimes look awkward on graphs.
The following columns are simply measures of the
brightness of three stars,
in INTENSITY units.
In other words, something like
"how many photons from this star struck the camera
during the exposure?"
If star A is twice as bright as star B,
then its intensity value in this datafile will be twice
as large.
Simple.
Here's a link to the first datafile you will analyze today.
-
Your first job is to compute the mean and standard deviation of
each star's intensity.
Write your results in a simple table, like this:
Star mean intensity stdev of intensity
-----------------------------------------------------------
A 997.6 31.8
B 550.6 23.7
C 160.0 12.8
-----------------------------------------------------------
-
Based on these values, which star do you think has been
measured most precisely?
Explain your reasoning.
Well, since the standard deviation of star A is largest,
perhaps star A has the least-precise measurements.
By this reasoning, since star C has the smallest standard
deviation, it might be the most precisely measured.
One might make a different (and better) argument -- see
the next time we ask this question.
Your next job is to create a simple light curve.
This is simply a graph showing the
brightness of each star as a function of time.
Create a single graph which has
intensity on the Y-axis and time on the X-axis.
On this graph,
plot the measurements for each star,
using dots/symbols for each measurement;
do NOT connect the data with lines.
Make sure that your graph clearly indicates
which symbols belong to star A, B, and C.
-
Make a light curve, showing intensity as a function of time.

- Look at this graph.
Based on the visual appearance,
which star appears to be measured MOST precisely,
and which LEAST precisely?
The symbols for star C appear to have the smallest scatter
around the average level, so it seems to be the most precisely
measured star. Star A, on the other hand, seems to be the
least precisely measured star.
- How does your answer to item D
compare to your answer to item B?
The answers are the same: star C appears to be the most
precisely measured.
(But keep an open mind ... and keep reading!)
When astronomers want to compare their results, they
convert optical measurements to magnitudes.
There are many steps involved in this procedure,
but we'll look at a simplified version for this exercise.
You will convert each measurement of intensity
into an
instrumental magnitude
using the following equation:
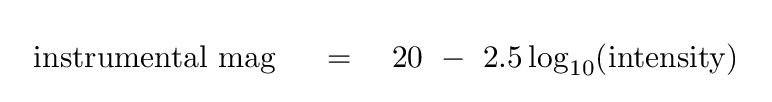
Use this equation to convert all the measurements of
intensity into instrumental magnitudes.
Then, use those magnitude values in the following steps:
- Make a new table which shows the mean and standard deviation
of each star's MAGNITUDE measurements.
Star mean mag stdev of mag
-----------------------------------------------------------
A 12.503 0.035
B 13.149 0.047
C 14.493 0.087
-----------------------------------------------------------
-
Based on these values, which star do you think has been
measured most precisely?
Explain your reasoning.
In this case, the standard deviation of the brigtness,
expressed in magnitudes, has the smallest value for star A.
Therefore, star A now seems to be the most precisely
measured star.
Your next job is to create another light curve.
This time,
however, instead of placing intensity on the Y-axis,
you must plot the instrumental magnitude values
on the Y-axis.
In order to put the brightest star at the top of the graph
(for easy comparison with the intensity graph),
you will need to REVERSE the order of the Y-axis:
large magnitude values should appear at the BOTTOM
of the graph, and small magnitude values at the TOP.
-
Make a light curve, showing magnitude as a function of time.

- Look at this graph.
Based on the visual appearance,
which star appears to be measured MOST precisely,
and which LEAST precisely?
The bright star A now appears to be measured most precisely,
and the faint star C now appears least precisely measured.
- How does your answer to item I
compare to your answer to items D and G?
This answer is the opposite to my answer for question D,
but the same as my answer for question G.
At this point, you may be a bit puzzled --
just what is the right way to estimate
the precision of a measurement?
Or, to put it another way,
how can we really determine the uncertainty in a measurement,
or a series of measurements?
One very good way to compare uncertainties
is to put them into a relative form.
Instead of talking about the actual value of standard deviation
in the intensity of a star,
one might express it
in PERCENTAGE terms.
In other words,
one might compute
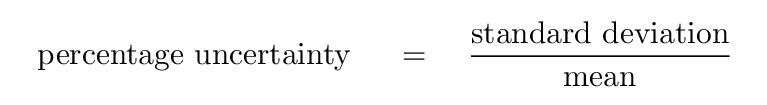
-
Using your values for the mean and standard deviation
of the INTENSITY of each star, compute a
percentage uncertainty in the mean value.
Write your results in a table:
Star mean intensity stdev of intensity percent uncertainty
-------------------------------------------------------------------------
A 997.6 31.8 3.2 %
B 550.6 23.7 4.3 %
C 160.0 12.8 8.0 %
-------------------------------------------------------------------------
-
Compare these percentage uncertainty values to the
standard deviation in the magnitude measurements.
Comment.
The uncertainties in magnitudes appear very close to the
percentage uncertainty in the intensities.
That turns out to be nice, convenient coincidence that
astronomers can use to their advantage.
- Which do you think is a better way to make light curves:
using intensity, or magnitudes?
Explain your answer.
Using magnitudes causes the percentage uncertainties --
which are meaningful measures of the precision of a
measured value -- to appear on a graph.
For that reason, light curves made with magnitudes,
instead of intensities, are probably more useful
in most situations.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.