Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Today, we'll look at the physics of an eclipsing binary star system, and figure out how to derive fundamental properties of a system -- the mass and size of the stars, for example -- from the quantities we can easily observe.
You already know what a star is. A binary star is simply a pair of stars which orbit around each other due to their mutual gravity.
Now, if we are very lucky, and the following conditions are ALL met,
then we can use geometry and one solid bit of physics -- the spectrum of radiation emitted by a hot gas -- to determine the masses and sizes of the stars, their temperatures, and even the distance to the system.
This is not such a common occurence. In many cases, we CAN'T tell that a tiny little dot of light in the sky is actually the combined light of two stars. Even when we can, in the overwhelming majority of cases, the plane of the orbit is NOT edge on, so we won't see the effects of one star blocking the other's light. Finally, even if we do notice the changes in brightness that reveal eclipses, we may not be able to measure spectra of BOTH stars. If we can only acquire spectra of one of the two stars, then we can't learn quite so much about the stars in the system.
But let's suppose that we happen to stumble across a system which meets all the conditions, allowing us to make light curves and high-quality spectra of both stars.
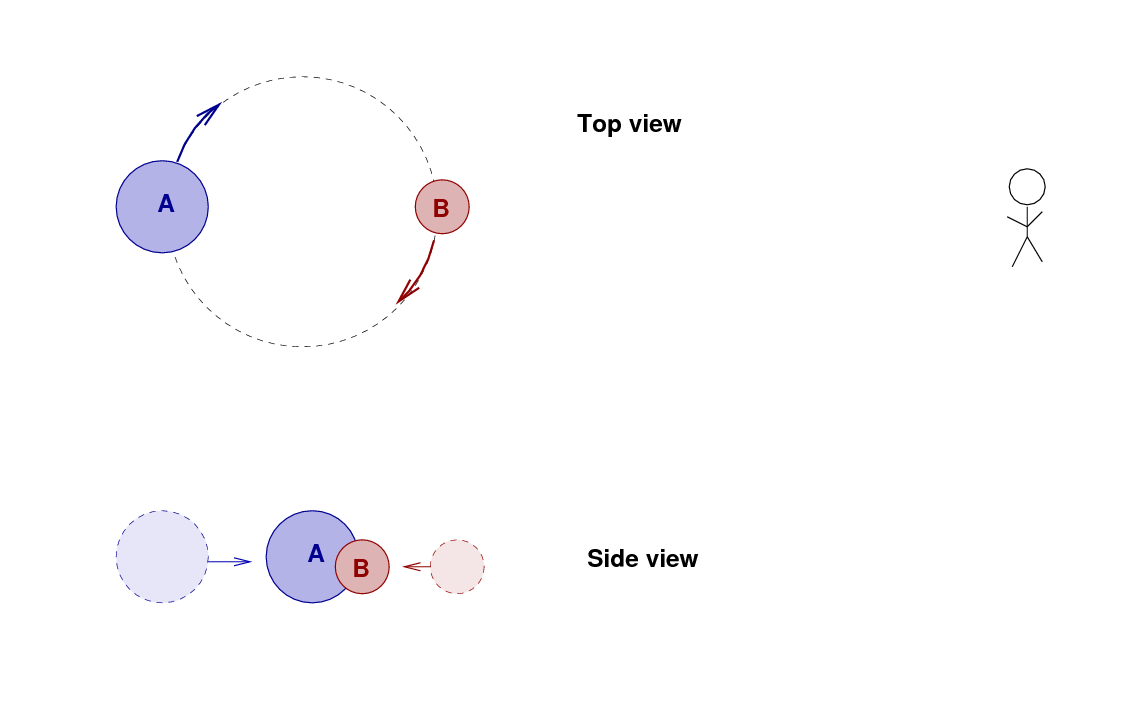
If we measure the light from the system over one full orbital period, then we'll see one dip in the brightness as star B passes in front of A, and then a second dip when A passes in front of B.
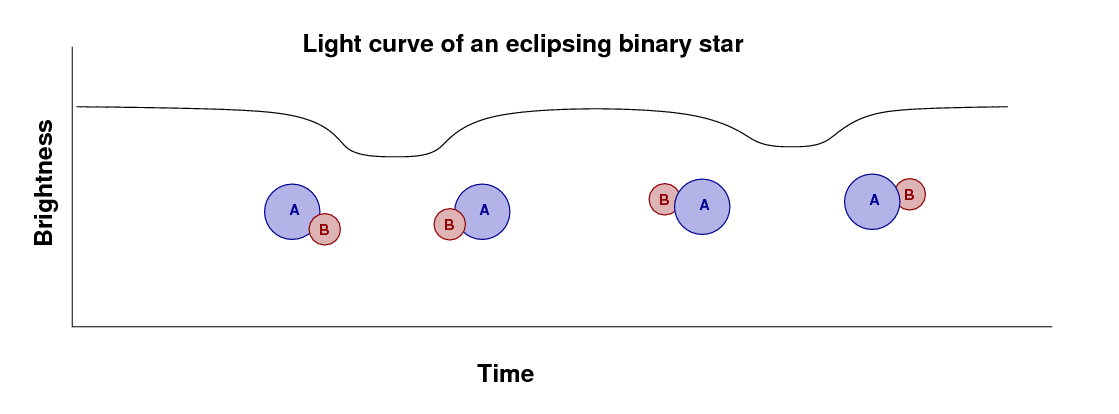
From the light curve, we can measure directly several useful quantities (which I'll define a bit later):
From other telescopes and the work of other scientists, we can measure (or look up) several other properties:
Let's pick one binary star system with a wealth of information, and use it to illustrate the methods needed to go from measurements to physical properties. The star we'll choose is KIC 8736245, described in this paper:
Our simplified calculations may not match the results reached by the authors of this paper, who do everything much more carefully and take no shortcuts.
The first and easiest (usually) aspect of a binary system to measure is the period of the orbit. We will use data collected by the the Kepler space telescope, which made very precise light curves. We can access some of this data at the following archive site:
Enter the name "KIC 8736245" into the "and enter target" box, then click on "Search".
When the search results appear, in the "Mission" panel, check the "Kepler" box (not the "KeplerFFI" box). A single item should apear in the "List View" panel. Click on the icon that looks like a small light curve -- it says "Timeseries Viewer" if you hover over it.
You should see a new window like this:
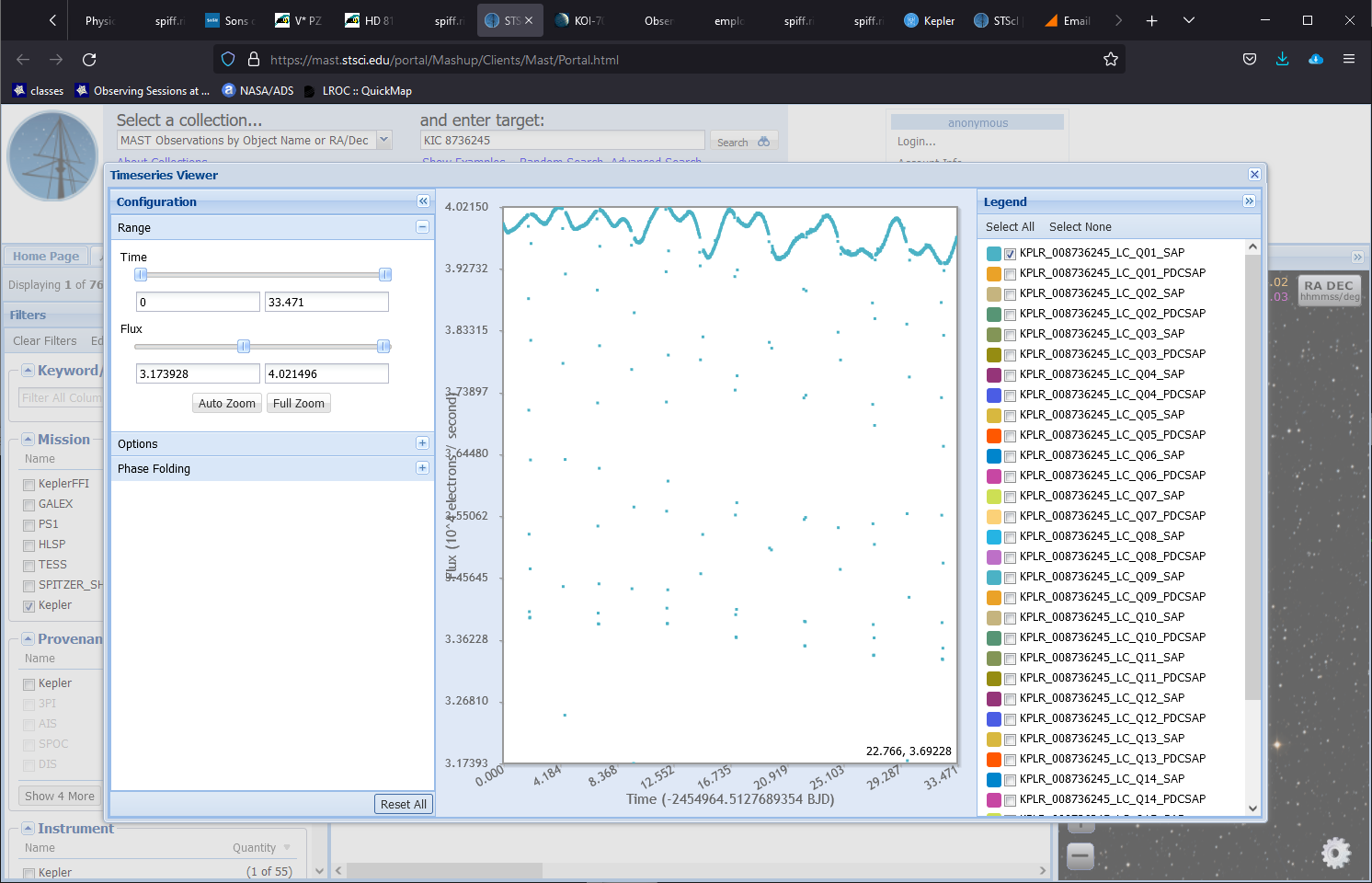
Your task is to measure the period of this eclipsing binary system. Note that the dips come in pairs: a deep one, then a shallow one, then a deep one, and a shallow one. A full period runs from deep dip to deep dip.
Q: What is the period of this star, in days? Write it down. Q: Convert the period to seconds and to years. Write down each.
Next, we will zoom in on just one primary dip. Each group should choose one of the deep dips. Use the sliders and controls in the panels on the left to zoom in one your dip, and measure two time intervals:
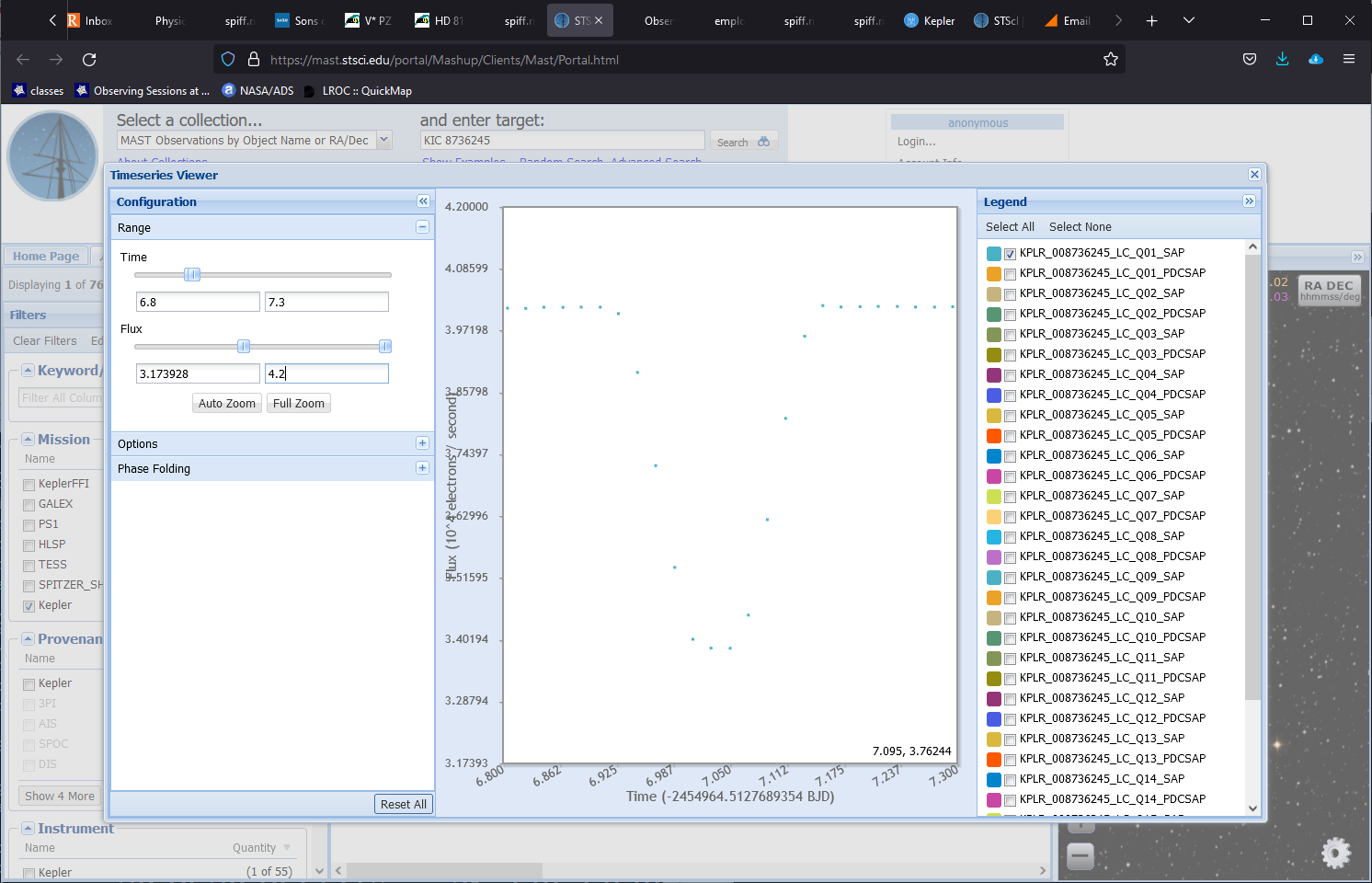
Q: What is the time interval at the TOP, in seconds? Write it down. Q: What is the time interval at the BOTTOM, in seconds? Write it down.
You can see that the light curve has a flat bottom; the light stays (nearly) constant during the middle of the dip. Why? Take a look at this close-up view of an eclipsing system. As star "A" moves to the left, and star "B" crosses in front of it to the right, we can identify four moments when the limbs of the stars first (or last) touch each other.
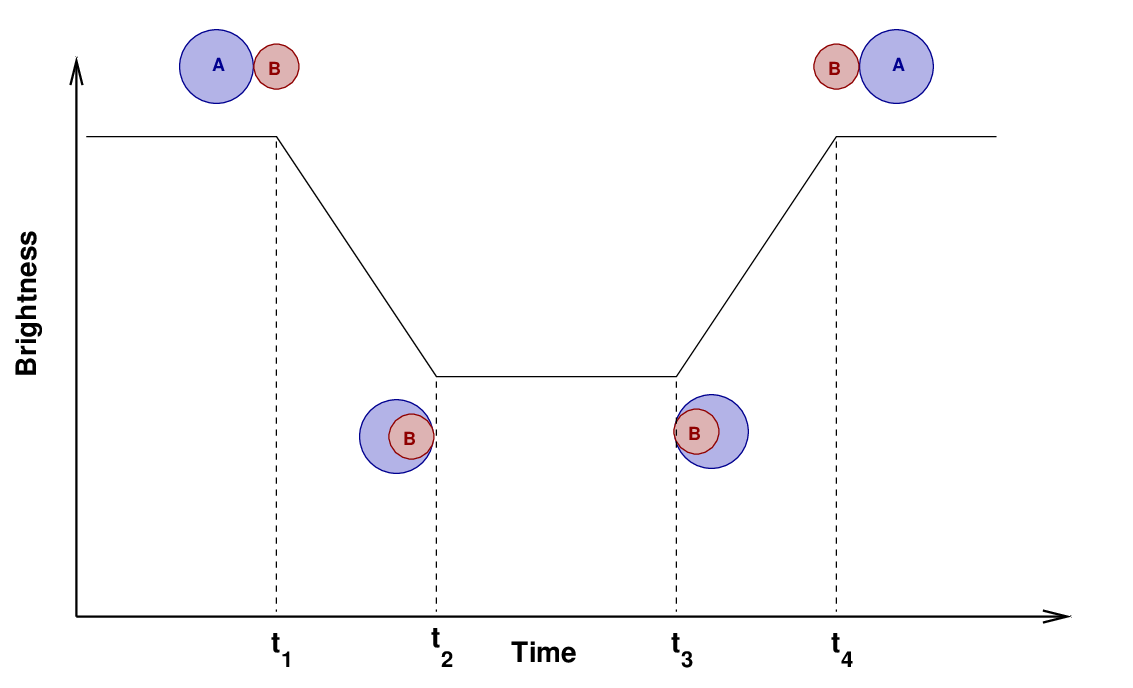
Your measurement of the duration at the TOP of the eclipse corresponds to (t4 - t1), and the duration at the BOTTOM of the eclipse is (t3 - t2). We will use these times to compute the SIZE of each star in a moment.
But first, we need another piece of information: the velocity of each star in its orbit. We can derive these speeds using spectra of each star measured at several locations in the orbit. The Doppler shift of the lines yield the radial velocities of each star -- that is, the motion of each one toward or away from us.
In this paper, Fetherolf et al. provide a nice graph showing the radial velocities at eight moments during the orbit. Note that the average speed of each star is not zero, but around +12 km/sec. That means that the entire binary system as a whole is moving away from the Sun at a systemic velocity of 12 km/sec.
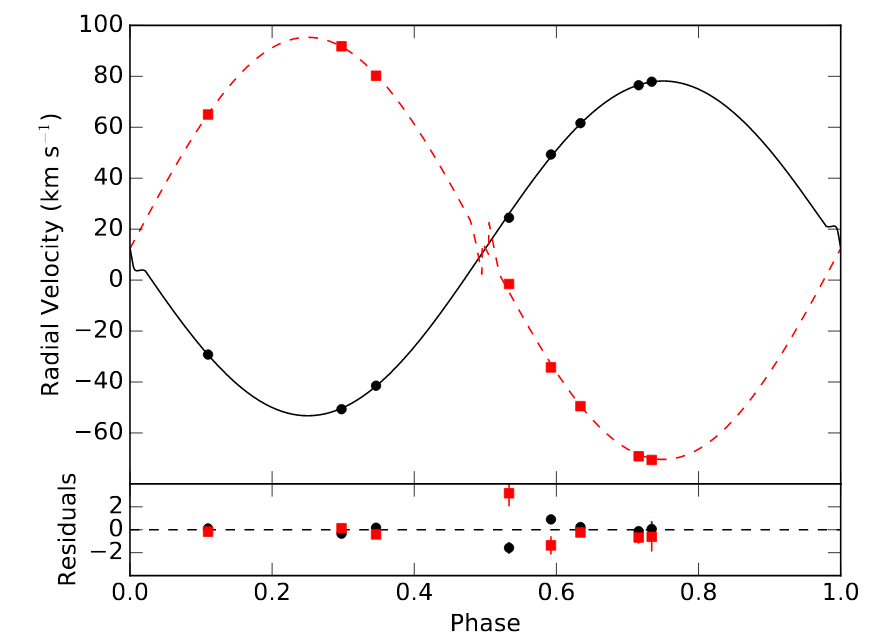
Figure 3a taken from
Fetherolf et al., AJ 158, 198 (2019)
Q: What is the amplitude of each star's motion? In other words,
what is the maximum speed away from the systematic velocity
for each star?
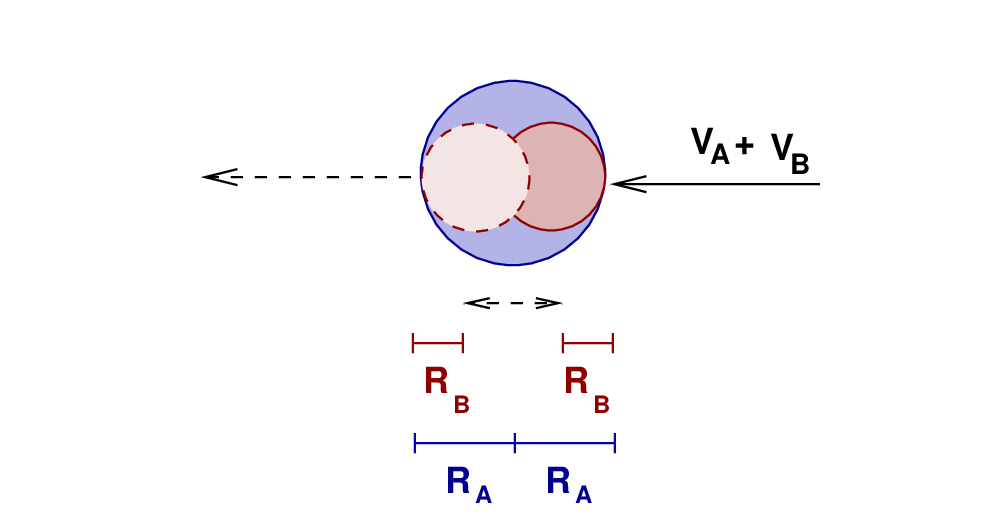
Right. We're almost ready to compute the size of each star. Look closely at the motion of the two stars as the eclipse happens. Since the two stars are moving in opposite directions as they pass each other, their RELATIVE speed is simply (vA + vB). Let's fix the star B in place, and watch as the star A moves across it from right to left at this combined speed. During the time period from first to fourth contact, the star A must move a distance of RB + RA + RA + RB.
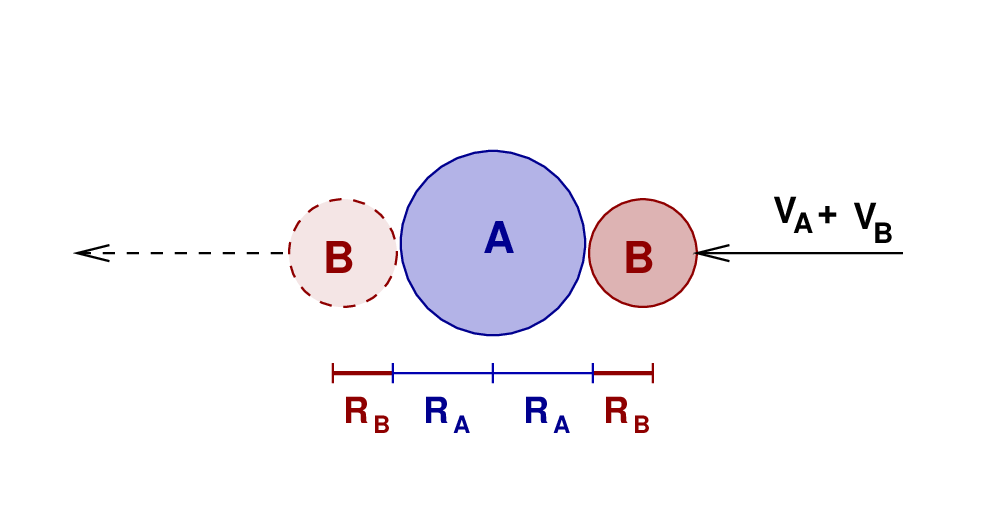
That means that we can find one equation for the radii of the stars.
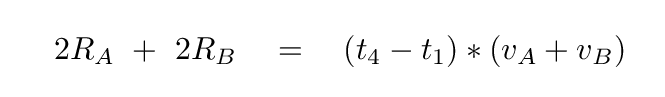
In a similar way, we can derive a second relationship involving the radii and the time between second and third contact.
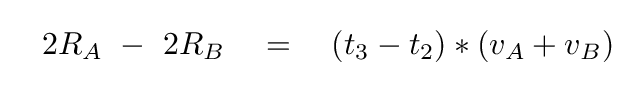
Hmmm. Two equations for two unknown radii. This is a job for linear algebra.
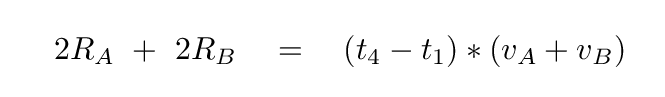
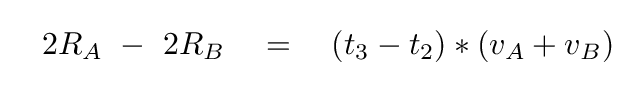
The solutions turn out to be:
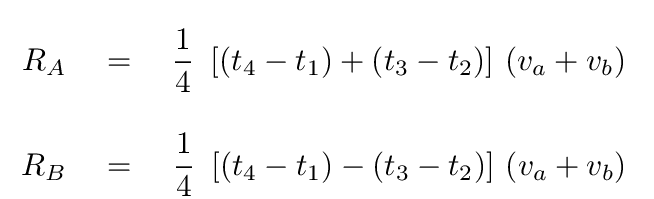
Okay! Using your measurements of the time intervals (t4 - t1) and (t3 - t2), and the velocities measured by Fetherolf et al., you can compute the size of each star.
Q: What is the radius of star A in km? Q: What is the radius of star B in km?
Our Sun has a radius of Rsun = 6.96 x 105 km.
Q: What is the radius of star A in solar units? Q: What is the radius of star B in solar units?
In order to compute the mass of each star, we will apply Kepler's Third Law. Kepler found a very simple relationship between the period and the size of an orbit:
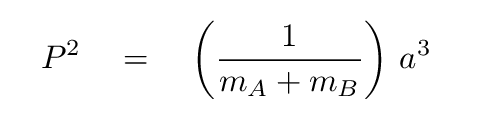
The period -- you've already measured that. But what is the semi-major axis?
In a binary star system, the semi-major axis is the separation between the two stars. If the two stars have different masses, then each will orbit the center of mass with a different orbital radius. The semi-major axis a is just the sum of these two radii.
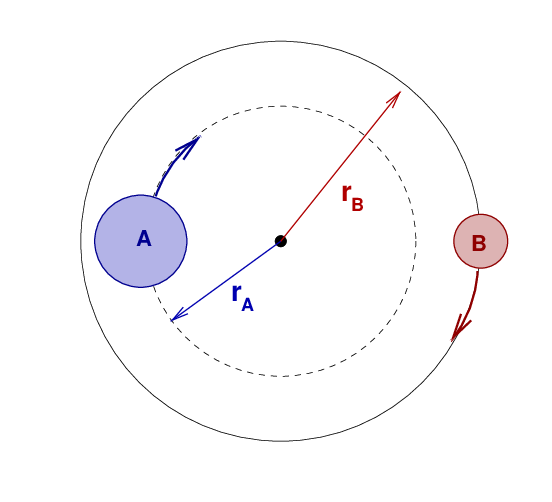
So, if we could figure out the orbital radius of each star, we could add them together to find a, and then compute the total mass using Kepler's Third Law. And we CAN figure out the orbital radii; here's how. We know how fast each star is moving, based on the radial velocity graph you examined earlier. We also how long it takes each star to complete one orbit: that's just the period. So, we can calculate the circumference of each star's orbit:
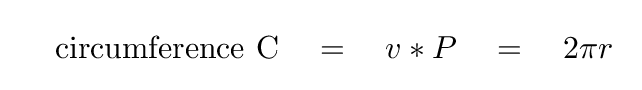
It's probably easiest if you use the period in seconds, and the velocity in km/sec.
Q: What is the radius of star A's orbit, in km?
Q: What is the radius of star B's orbit, in km?
Q: What is the semi-major axis, in km?
The average distance between the Earth and Sun is known
as 1 Astronomical Unit, or 1 AU for short. To a rough
approxmation,
1 AU = 1.5 x 108 km
Q: What is the semi-major axis, in AU?
Great! Now we can compute the mass of the two stars added together using Kepler's Third Law:
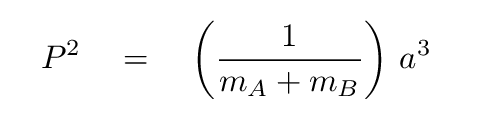
Q: What is the mass of the two stars added together?
Express the result in solar masses.
But we want to know the mass of each star individually, too. Fortunately, we already possess a clue that provides the answer. The radial velocity measurements showed that one star moved more quickly than the other.
Figure 3a taken from
Fetherolf et al., AJ 158, 198 (2019)
Why is that? Because the gravitational force is the same on both stars, the less-massive object will be given a larger acceleration, and thus a larger velocity. It's a simple relationship:
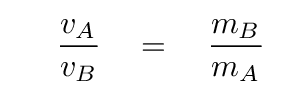
Q: Use this relationship, and the velocities you measured earlier
to determine the ratio of masses.
Q: Use the ratio of masses, and the total mass you calculated,
to determine the mass of each star.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.