Converting between coordinate systems
Suppose that you know the coordinates of an object in one system, but you need to know its coordinates in a different system. For example, someone tells you that you should consider using HST to study a quasar located atRA = 18:14:15 Dec = -29:03:39
Is this a good idea? The equatorial coordinates don't reveal any information about the question, in either a good way or a bad way -- but, as you will see, expressing the coordinates in another system WILL tell us something useful.
We'll talk about three other systems today: one based on the motions of the Sun and planets in the sky, one based on the Milky Way Galaxy, and a third is a slight tweak on the familiar (RA, Dec) system. In order to switch back and forth between coordinate systems, I recommend one of these tools:
- NED's coordinate converter (runs in a web browser window)
- Stellarium (stand-alone planetarium program)
The ecliptic coordinate system is convenient when
dealing with objects in the solar system:
they are concentrated towards the ecliptic equator:
If you zoom in, you can see that the major planets
lie slightly above or below the ecliptic equator,
because their orbits around the Sun are inclined
slightly with respect to the Earth's.
Click on the image below to start an interactive
view of the orbits of the planets.
Ecliptic coordinates can also be important when you
want to avoid objects in the solar system.
Telescopes in space, such as the Hubble Space Telescope
or the Chandra X-ray Telescope,
cannot point close to the Sun
(or else they might suffer damage to their detectors).
For some purposes, astronomers want to make very,
very long exposures: days or even weeks long.
During such a long exposure, the Earth may move a
significant fraction of its entire orbit,
which can cause a target originally far from the Sun ....
... to move closer to the Sun, from the telescope's point
of view.
Therefore, astronomers sometimes choose their
very deep fields
The Sun isn't the only source of problems for telescopes
within our solar system.
In addition to the planets and asteroids,
innumerable tiny particles of dust also orbit the Sun.
In the optical portion of the spectrum,
these particles are nearly invisible.
But in some portions of the infrared,
the amount of energy they radiate via
blackbody thermal emission can create
an important background;
we call this
zodiacal light.
In the image below, the light-blue S-shaped curve
running through the center is due to
dust in the plane of the solar system.
On a warm July evening in Rochester, the Milky Way
stretches overhead, with the galactic center
just above the southern horizon.
If you make a map of the sky in galactic coordinates,
the Milky Way runs right across the middle.
The section we see in the summer sky from Rochest is
in mostly the left half of this map.
An infrared map of the sky in galactic coordinates
made by the COBE satellite is dominated by emission
from dust in the Milky Way,
but also shows a faint band of light
due to emission by dust particles in the
solar system.
Note that the plane of the solar system is tilted by almost
ninety degrees relative to the plane of the Milky Way.
Astronomers who wish to see very distant objects --
galaxies and quasars far beyond our own galaxy --
must avoid the dust clouds which lie along the
plane of the Milky Way.
They prefer to point their telescopes far above
or far below the galactic equator.
Remember that quasar that some asked you to observe with HST?
Its coordinates are
If you need to acquire measurements of an object
in the sky,
you might find it useful to convert the
usual (RA, Dec) coordinates into a slightly
different pair:
(HA, Dec).
The "HA" stands for Hour Angle.
What's that?
Let's go back to looking at how objects move across the sky.
Suppose we were planning to use our telescopes this evening
in order to take images of the Orion Nebula,
aka
Messier 42,
or M42 for short.
If we go outside at 7 PM = 19:00 local time and look south,
we'd see Orion in the eastern half of the sky.
We certainly COULD take a picture of the nebula at this time;
its clearly up above the horizon.
But ... is this the best time to take a picture of it?
The basic motion of objects in the sky is:
rise in East, set in West.
So we expect the nebula to follow a path sort of like this:
In general, the best time observe objects is when they
are highest in the sky.
At that time, their light passes through the smallest volume
of the Earth's atmosphere on its way to our telescopes
and cameras.
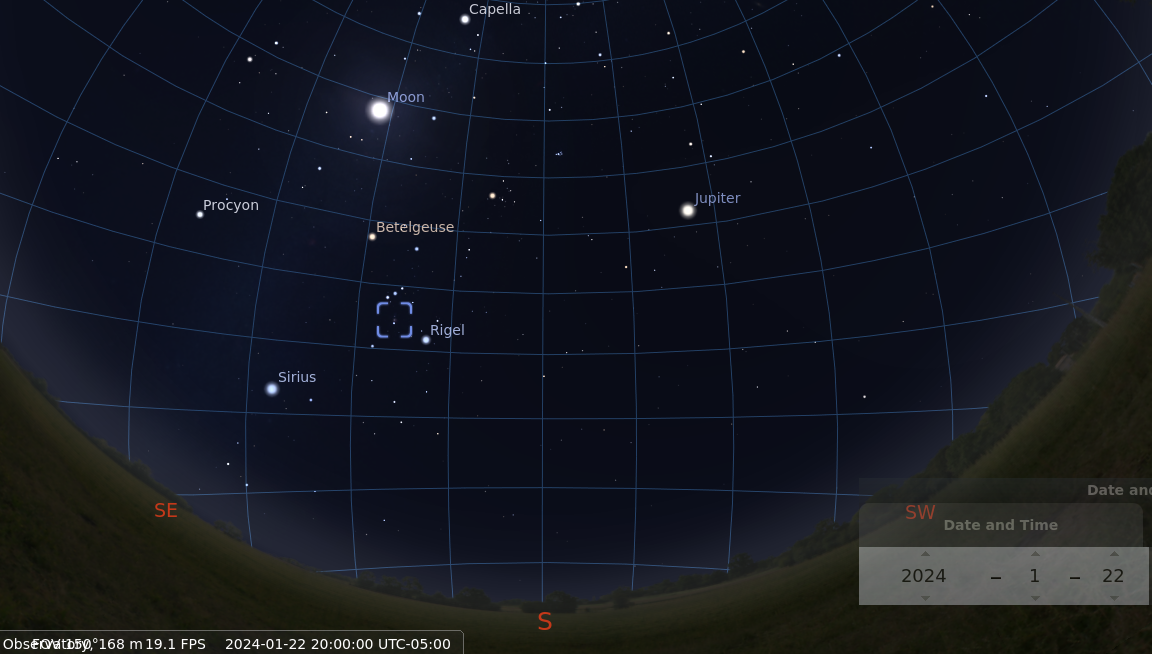
Right now, at 7 PM = 19:00 local time,
is clearly a bit too early.
Should we wait until 8 PM? Or 9 PM? Or maybe midnight?
Let's see ...
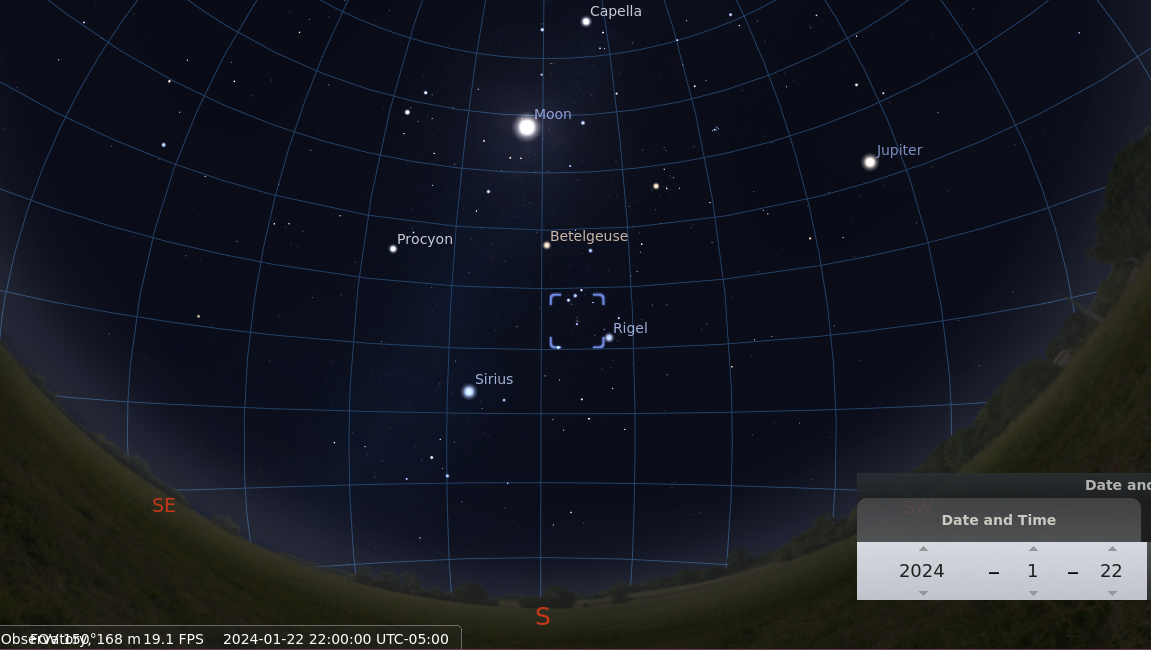
here's the view at 8 PM = 20:00 local time ...
and at 9 PM = 21:00 local time ...
and at 10 PM = 22:00 local time ...
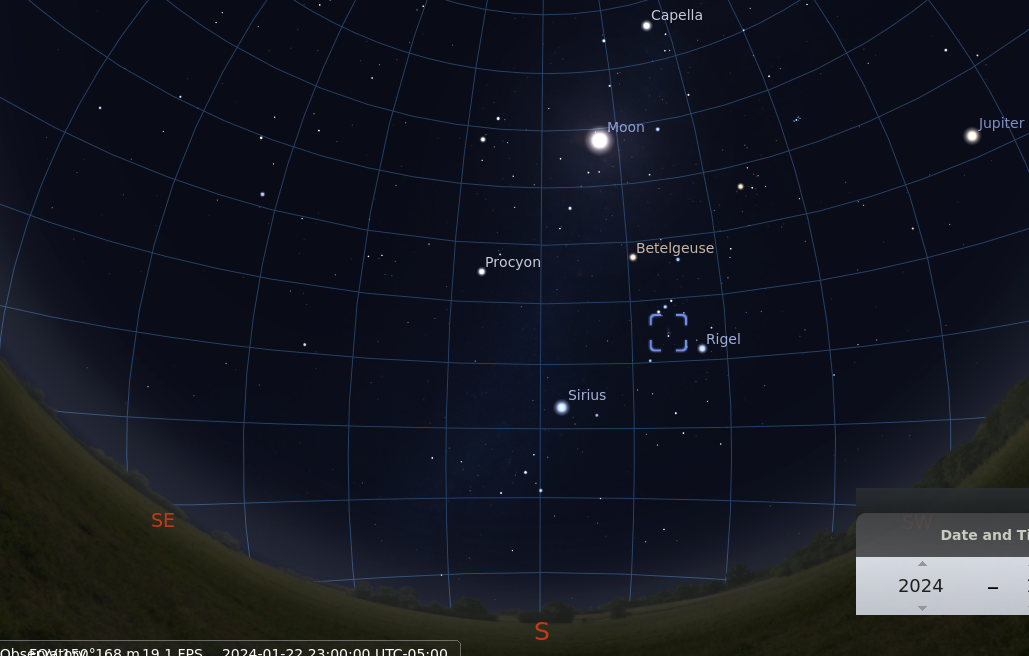
and at 11 PM = 23:00 local time ...
Hmmm. It seems that somewhere between 10 PM and 11 PM,
(between 22:00 and 23:00 local time)
was probably best.
But making this determination was a bit of a pain:
I had to generate pictures of the sky for a range of
times, and examine each one to see where
M42 happened to be.
Is there some easier way?
Let's go back to our first view at 7 PM = 19:00 local time.
It turns out that stars will reach the peak of their
trajectory across the sky when they are located
due South (or, for observers in the southern hemisphere, due North).
Astronomers call the line which runs due South
the "meridian".
If we watch M42 over the next few hours,
we will see it approach the meridian,
rising higher and higher in the sky as it goes.
But how long will it take to reach the meridian?
Any observer would love to know this interval --
it tells her how long she ought to wait in order
to achieve the best results.
And that is exactly how Hour Angle is defined.
Look again at the position of M42 at 7 PM = 19:00 local time.
The grid shown covering the sky is the grid of Right Ascension
and Declination.
The lines for Right Ascension are spaced at intervals of one hour.
We can see that M42 is located about 2.5 hours of RA
to the East of the meridian.
That means that at this moment,
the hour angle of M42 is HA = -2.5.
Last modified by MWR 1/15/2024
Ecliptic (Solar System) coordinates
For objects within our solar system --
planets, asteroids, comets --
it often helps to use a coordinate system
centered on the Sun, with its equator running along
the plane of the planetary orbits.
We call this the ecliptic coordinate system.



Image courtesy of
JPL Horizons' orbit viewer

Q: Read this article to find the equatorial coordinates
of the Hubble Deep Field (hint: look in Table 1). What is the
(RA, Dec) center of the field?
Q: What are the ecliptic coordinates of the field?
Q: How close could the Sun come to this region?

IRAS all-sky image courtesy of
NASA/JPL-Caltech
Galactic Coordinates
One more set of coordinates comes into play
if one studies the distribution of stars
within our Milky Way Galaxy,
or the distribution of other galaxies
in the far reaches of space.



Map courtesy of the
Lund Observatory

Q: What are the galactic coordinates of the Hubble Deep Field?
Q: What is the angular distance between the dust clouds of the Milky
Way and the Hubble Deep Field?
RA = 18:14:15 Dec = -29:03:39
Q: What are the galactic coordinates of this object?
Q: Is it a good idea to apply for time on HST to observe this quasar?
Explain why or why not.
Hour Angle -- a "local" version of Right Ascension

Image courtesy of
NASA, ESA, M. Robberto (Space Telescope Science Institute/ESA) and the Hubble Space Telescope Orion Treasury Project Team

Q: Is this the BEST time to image M42? If not, why not?

Q: How long must we wait until M42 is at its peak?

YES! Use Hour Angle!

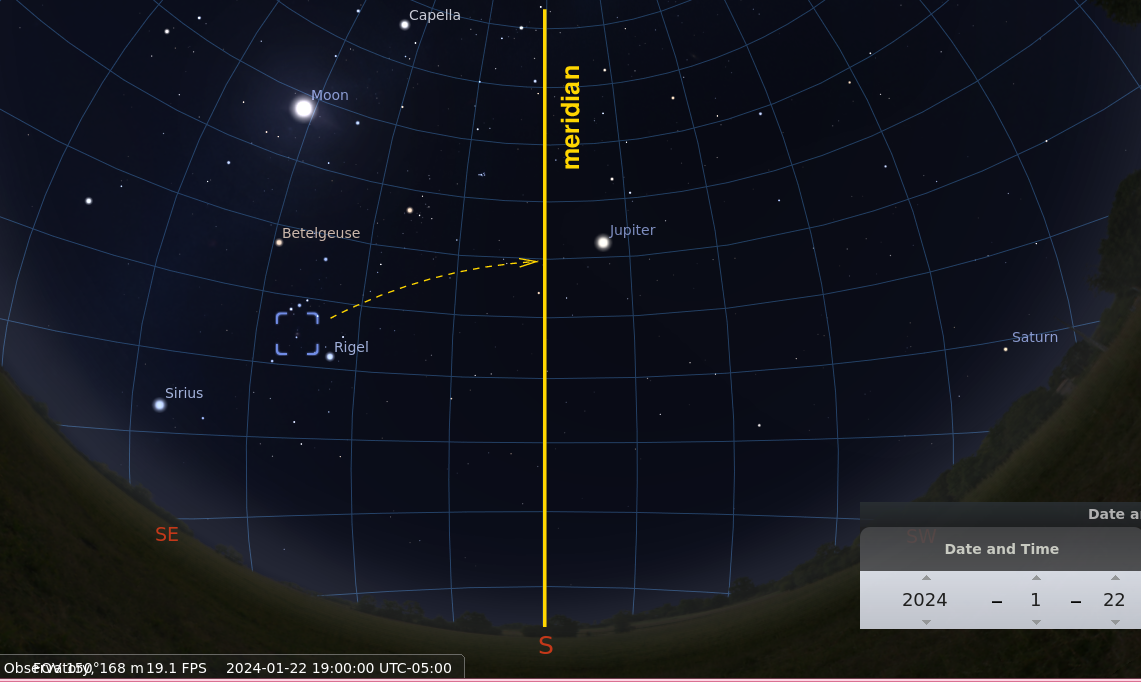
Hour Angle (HA) is defined as the time, in hours, until an object crosses the meridian
if HA < 0 or HA > 12 it denotes the time remaining until reaching the meridian
(meridian at HA = 0 or HA = 24)
if HA > 0 it denotes the time passed since crossing the meridian


Q: When will M42 be highest in the sky?
Q: The Declination of M42 is Dec = -5 degrees. When it crosses the
meridian, how high above the horizon will the Orion Nebula appear?
My answer
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.