Flatfield images

Today, we're going to look at the issue of "flatfield images". What are they, and why do we need to take them? What can we do with them?

The images for today's exercises can be found in the $dd/sep20_2003 directory. Make sure that you make copies of all these images in your own directory. So, after you log in, you might execute these commands, which

change to my home directory
list all the files there
remove them (since they aren't needed for today's class)
copy all the files from the $dd/sep20_2003 directory
list all the files -- which we will use today

When you have reached this point, please pause, and look around. If someone nearby is having problems, please help him or her to reach this point.

Examine carefully the background of a raw image

Today, let's take another look at one of the "target images" take on Sep 20, 2003. Make sure that you have a fresh copy of the file v585.fit in your directory.

Astronomers typically display images in an inverted mode, so that stars appear as black objects on a white background. It's easier to pick out very faint detail that way. So, display the target frame like so:


        tv v585.fit z=900 l=1000 invert

It should look like this:

Hmmm. There are lots of hot pixels, but we know how to get rid of them. Is there anything ELSE wrong with the image?

Display the image again, this time with a much smaller range, l = 100 instead of l = 1000. This will enhance very subtle features in the background.


        tv v585.fit z=900 l=100

Note that you don't need to (and shouldn't) provide the invert keyword this time; the tv command remembers the display mode and keeps using the last one you specified.

Display the image with the parameters shown above.
What sort of defects or funny things do you see?

When you reach this point, stop and look around. If someone nearby hasn't reached here yet, offer to help. If someone nearby has reached this point, too, then discuss your answers.

Variations in sensitivity across the focal plane

The problem is that some (all?) instruments are imperfect. When I write "instruments", I mean the combination of optics and detector. Several different problems commonly cause variations in sensitivity across the focal plane; if those variations are not corrected, they end up as errors in the measured magnitudes of stars and other celestial sources.

The three main culprits are

vignetting in the optics
intrinsic and surface defects of the CCD
shadows cast by dust

Vignetting

A perfect optical system would lead every incoming photon to its proper place on the focal plane. If pointed at a uniform source of diffuse light, the entire focal plane would receive equal amounts of light. In the real world, some portions of the focal plane get more light than others. Usually, the central portions get a bit more than the outer edges.

Here's an example: a raw I-band image taken by one of the TASS Mark IV cameras . The field of view is very large, about 4 degrees on a side.

You can download and examine the image itself, if you wish. Be careful, though: it's a big image, roughly 2048x2048, so if you want to see the whole thing, you'll need to use zoom=0.25 as part of your tv command.

right-click to save the image "tass_i.fit"

Intrinsic and surface defects of the CCD

Sometimes, one region of the silicon is just more sensitive to light than others. Thinned, back-illuminated chips are prone to showing artefacts due to the grinding, polishing and etching of their surfaces.

Some CCDs may have been nearly perfect when first made, but, over the years, have accumulated layers of oil, grease, or other contaminants. Little specks of dirt and dust can also sit on the chip, blocking most of the light from reaching the pixels below. Here are a couple of closeups of quadrants 1 and 2 of the Dandicam CCD camera.

Dust particles in the optical path

Dust gets everywhere. Any particles which stick to the optical surfaces -- the lenses a focal reducer or field flattener, or the optical window in front of the CCD itself -- will cast shadows on the focal plane. Diffraction turns these shadows into the oh-so-familiar "dust donuts". Here are examples from the MDM 1.3m telescope at Kitt Peak:

and the 1-m telescope at Las Campanas in Chile:

The "Flatfield" -- in theory

The problem boils down to this imagine a very simple CCD, consisting of just two pixels. Suppose that the pixel on the left is a bit less sensitive than that on the right. I point my camera at a blank white wall. I ought to see this:


             left pixel              right pixel
           --------------         ----------------
              100 counts             100 counts

But instead, the CCD actually records this:


             left pixel              right pixel
           --------------         ----------------
                95                      100

Evidently, the left-hand pixel is slightly less sensitive to light, by 5 percent. This is a problem if we're trying to make precise measurements of stellar brightness. Suppose I look at two stars, A and B, which are really the same brightness. But if star A falls on the left-hand pixel, and star B on the right-hand pixel, I won't see that; instead, I will measure fewer counts from star A:


              star A                   star B   
           --------------         ----------------
               9,500                   10,000

Is there any way to correct the measured quantities so that they accurately reflect the actual incoming signals from the stars?

Sure! It's not too hard, either. All I need to do is divide each pixel's measured value by its relative sensitivity, like this:


              star A                   star B   
           --------------         ----------------
 measured      9,500                   10,000  

            divided by              divided by 

 relative
 sensitivity     0.95                    1.00

            ===========             ============

  corrected   10,000                   10,000

So, the theory of "flatfields" goes like this:

Before the night starts ...
- take a picture of a uniform, bright scene: a "flatfield image"
- use the pixel values of this "flatfield" to define the relative sensitivity of each pixel
During the night ....
- take pictures of stars, galaxies, etc.
Afterwards ...
- divide the pictures of stars by the "flatfield" image to correct for differences in sensitivity

The Flatfield -- in practice

There are a few complications:

Where can you find a uniform, bright source of light?

There are two common methods. The first is take pictures of the sky around dusk or dawn: "twilight flats". It's tricky, because there's only a brief period of ten minutes or so during which the sky remains bright enough to hide stars, yet faint enough to prevent the CCD from saturating. The other idea is to take pictures of a blank screen or panel attached to the inside of the dome: "dome flats." You have much more control over these.

How high does the signal have to be in a flatfield image?

The statistical variation from one picture to the next will scale as the inverse square root of the number of electrons recorded in each pixel. If each pixel has 100 electrons, then a rough estimate of the random variation in each pixel's value (from one picture to the next) is


                 uncertainty = 1.0 / sqrt(100)

                             =  0.1   =  10 percent

If you want to do work at the 1 percent level, you need to gather roughly 10,000 electrons in each pixel of the flatfield image.

It's a bit more complicated than this, but a good rule of thumb is "take flatfield images which are around 1/4 to 1/2 of the saturation level." For the RIT cameras, anywhere between 10,000 and 20,000 counts per pixel is pretty good.

How can you get a true measure of sensitivity to LIGHT?

You have to remove

the zero-point value (which appears in zero-second dark exposures)
the electrons knocked free due to thermal motions (which grow with time)

If you don't, they your map of sensitivity isn't accurate.

Fortunately, this is easy to fix: just take a set of dark frames with the same exposure time as your flatfield images, create a master dark, and subtract that master dark from all flatfield frames before any further processing.

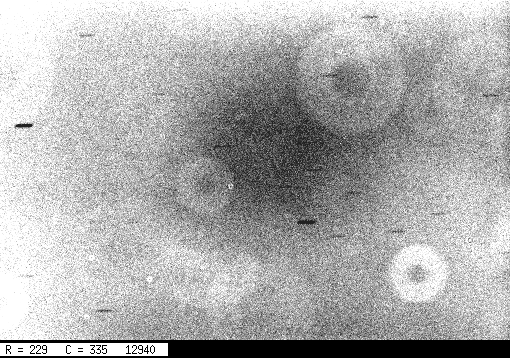
How can you avoid cosmic rays, or other contamination?

This is important, especially if you take twilight flats. Look at this example of a twilight flat taken at the RIT Observatory on Sep 20, 2003:

The short horizontal streaks are due to stars which were bright enough to appear above the relatively bright sky level. They are trailed because the telescope's tracking was turned off (oops).

Again, there is a relatively simple solution: take a number (10 or more) of flatfield images, and (after subtracting the master dark from each one) create a "master flat" by taking the median of the set, on a pixel-by-pixel basis.

Create a flatfield frame for Sep 20, 2003

Okay, so give it a try. Do the following:

make sure that you have the files from the sep20_2003 directory with names like flatclear_x*.fit and like dark4_*.fit; they are dark frames with the same exposure time (4 seconds) as the flatfield frames
display one image, flatclear_x_001.fit. Look at it with different contrast levels -- note the typical pixel values. What is the mean pixel value in the entire image?
use the median command to create a "master dark" from the 4-second dark exposures. What is the mean value of this "master dark" image?
subtract this "master dark" from each of the flatfield images
display the image flatclear_x_001.fit again and verify that the typical pixel levels are now a bit lower than they were originally. What is the mean pixel value in the entire image now?
calculate the mean value of each flatfield image, using the mn command. Make sure that you have already subtracted the dark frame first. If you want to avoid having to type 10 different commands to run the mn program 10 times, you might try this shortcut:

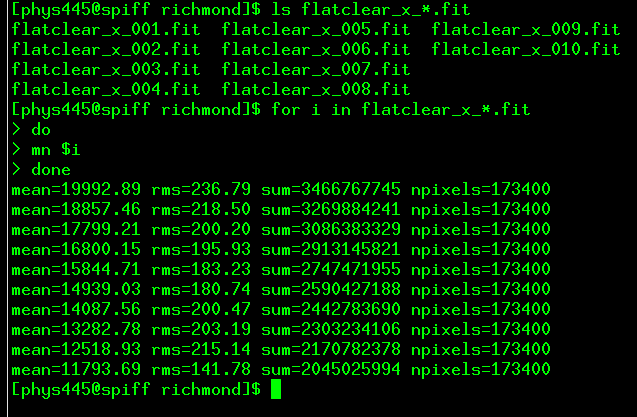
Notice that the mean level in each image decreases through the sequence. The sky was getting darker as I was taking these images. If we tried to compute a median value for one particular pixel -- say, (100, 100) -- from these images in their current state, we'd have a problem: that pixel would always be brightest in the the first image, and faintest in the last image, just because the average light level is highest in the first image.
use the median command to create a "master flat" from all the dark-subtracted flatfield frames. Run the command like this, in order to see what it is doing explicitly:
```
               median flatclear_x_*.fit outfile=master_flat.fit verbose
    
```
The median command will first re-scale all the flatfield images so that they have the same average value; only then will it look at each pixel to pick the middle value from the entire set of images. In order to do this re-scaling properly, the median program uses the results of the mn commands you ran earlier.
run the mn command on your "master flat" image, like this:
```
               mn master_flat.fit
   
```
to compute the average value of pixels in the "master flat"; we'll need that later ...
display this "master flat". How does it look? If you display the "master flat" right on top of the image flatclear_x_001.fit, then flip the two images to bring each to the front quickly, you'll get a VERY good idea of the difference between them. Click on the image below to see a blinking comparison of a single flatfield image and the master flatfield image.
you should see a "dust donut" in the lower-right corner of the flatfield frame. By what percent does the sensitivity change as you go from outside the donut, to the ring itself, to the interior of the donut?
compare the typical pixel level near the center of the image to the pixel values in the upper-left corner. By what percentage does the sensitivity change?

Now, with both a "master dark" image, and a "master flat" image, you are ready to reduce the raw target image of V585 Lyrae. This is the same procedure you'll use on your own target images.

make a copy of the v585.fit image, just in case something goes wrong.
```
        cp v585.fit v585_raw.fit
```
the v585.fit image has an exposure time of 30 seconds, so you'll need to create a master dark frame from the dark images which have an exposure time of 30 seconds.
```
        median dark30*.fit outfile=master_dark_30.fit
```
subtract this "30-second master dark" image from the v585.fit image
divide the dark-subtracted v585.fit image by the "master flat" frame. The command to do this looks something like
```
        div v585.fit master_flat.fit flat
 
```
Don't forget the final keyword flat at the end of this command!
display the processed and raw versions of the target frame side-by-side. Look at them carefully. Vary the display parameters l= and z= of the tv command to highlight faint features in the background.

If all went well, you should see faint defects in the raw image -- variations in the background level from center to corners, and dust donuts -- but no such defects in the processed version. Did it work?

For more information

The Observational Mishaps page is full of wisdom and experience.