Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Parallax is a great method, though properly accounting for the bias induced by random errors can be tricky. Alas, even the best modern instruments cannot measure distances to stars half-way across our own Milky Way Galaxy. If we want to make a real map of our own galaxy -- let alone anything OUTSIDE our galaxy -- we need to modify our methods.
So, today, we'll take the second step up the distance ladder: extrapolating from nearby stars to more distant spectroscopic "twins" and "cousins", using the inverse square law.
If we want to measure distances to stars more distant than those for which parallax is reliable -- in other words, if we want to measure distances larger than a few hundred pc (as of 2017) -- then we have to give up a precious concept: that of absolute distance. Everyone agrees on the size of our Solar System and the length of the AU, and everyone accepts the simple trigonometry involved in the calculation of parallax, so the results of Hipparcos or Gaia are treated as "absolute": they rely on so few assumptions that, as long as the measurements are adequate, one can trust them completely.
But when we move up the next step of the distance ladder, we find ourselves considering relative distances. In every case, we will only determine the distance to object B in terms of the distance to some closer object A.
For example, we might measure the distance dA to a 100-Watt light bulb in our house, and note its brightness.
then carefully measure the brightness of a distant 100-Watt light bulb, at some unknown distance dB
We can then use the inverse square law to compute the distance to the far-away light bulb:
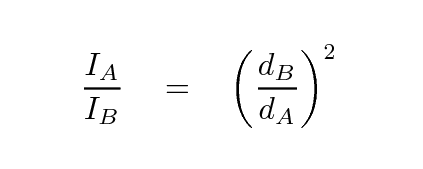
Of course, this means that any errors in the distance to A affect our estimate of the distance to B. That's the price of using relative distances, and the reason why the distance ladder becomes progressively less and less secure at larger distances.
One way to proceed is to pick one nearby star A, to which we have a precise distance from parallax, and one distant star B, to which we wish to determine the distance. In order to use a simple inverse-square law equation to compute the distance to B, we must pick stars which have the same luminosity. How can we do that?
Well, the best we can do is to pick two stars which are as similar in possible in
In most cases, though, when we try to find a nearby match for some distant star, we can only locate a star with approximately similar properties: a "cousin", rather than a "twin", if you like. That means that the two stars will probably not share exactly the same luminosity -- which means that our method to determine the relative distance will have some error.
Let's give it a try to see how well it works.
For our nearby star A, let's pick the Sun! We know the distance to the Sun perfectly (for all practical purposes), and we can measure all its properties very, very well.
For our distant objects B, I've chosen two stars which should be very good matches. They are "solar twins", taken from
The authors use very careful measurements of high signal-to-noise, high spectral resolution data to confirm 3 solar twins from one source, and identify 6 new solar twins from another. All the data is very high quality, so these matches are about as good as one can find. This is a "best case scenario" for measuring distances with a single pair of stars. Here are the two stars I've chosen from their set to compare to the Sun.
We'll start by making a table of the properties of these stars. I'll fill in the information for the Sun, using the apparent magnitude given by ( Mamajek's Star Notes); half the class will find the data for HD 78660, and the other half for HD 183658. First, we need to fill in the apparent V magnitude column. I recommend that you look in the Hipparcos catalog to find the Vmag (magnitude in Johnson V-band) for each star.
star apparent V magnitude distance (pc)
-----------------------------------------------------------------------
Sun -26.71 +/- 0.02 4.84813 x 10-6
HD 78660
HD 183658
-----------------------------------------------------------------------
Q: What is the apparent V-band magnitude of your star,
based on the Hipparcos catalog?
You should end up with these apparent magnitudes:
Hipparcos catalog distance (pc) based
star apparent V magnitude on inverse square law
-----------------------------------------------------------------------
Sun -26.71 +/- 0.02 4.84813 x 10-6
HD 78660 8.34 +/- 0.02
HD 183658 7.27 +/- 0.02
-----------------------------------------------------------------------
Okay, once we've filled in the V magnitude column, it's time for you to figure out the distance to each of the solar twins, using the inverse square law.
Not sure how to find distance? Look here
Q: What is the distance to your star, using the inverse square law?
How well did this method work? We can find out by comparing these results to the distances derived by a better method: trigonometric parallax. It turns out that both of these stars are close enough, and bright enough, to have good measurements in the Hipparcos catalog.
So, please use the Hipparcos catalog to look up the parallax for each solar twin, and then compute its distance using that value.
based on based on mags
parallax and inverse square law
star parallax (mas) distance (pc) distance (pc)
------------------------------------------------------------------------
HD 78660
HD 183658
------------------------------------------------------------------------
Finished?
When you are ready, you can see how your calculations compare to mine.
So we find that using the relative brightnesses of two stars, which we ASSUME to be identical, to compute their relative distances, sometimes yields the same answer as the (better, in general) trigonometric parallax technique ... but not always.
The trouble is that it's very difficult to find two stars which are perfect matches. And even if you can find an exact match, making a small random error in your measurement can ruin the result.
And what happens if you find a very distant star that has a spectral type which doesn't match any nearby star with a good parallax measurement? Without a good "cousin", this method can't be used at all.
Just how far can we trust the "spectroscopic parallax" method? It's hard to make any blanket statements, but easy to try a random experiement or two. Let's give it a try and see how well it does.
A0 V
mV = 0.03 parallax = 128 mas
7.76 pc
(m - M) = -0.55 MV = +0.58
Pause for a moment. What we've done so far is to establish the absolute magnitude MV of stars with some particular spectral type. We can then use this information to estimate the distance to any other star with the same spectral type.
Okay, let's try it. We need another random star with the same spectral type.
HD 5031 HD 22401
mv = 7.45
How well did our "spectroscopic parallax" method agree with the trigonometric parallax?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.