
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Back in the 1920s, an astronomer in California named Edwin Hubble was in the right place at the right time. The hot topic in astronomy was "galaxies" -- what were they, and how far away were they? Just a few years earlier, the astronomical community was split on the question "Are galaxies clouds of gas and stars within our own Milky Way, or are they independent structures, outside the Milky Way and equally large?" Scientists were coming to a consensus that they were outside the Milky Way, and perhaps just as big -- but they didn't have any good measurements of distance, so they couldn't be sure.
Hubble realized that he had the resources to answer these questions. He worked at the Carnegie Institute in southern California, which had two of the most powerful telescopes in the world at that time:

Hubble started a long-term program to study galaxies with these instruments, with the goal of measuring two quantities in particular:
This was no easy task.
How did Hubble determine the distances to galaxies? As described in Hubble and Humason, ApJ 74, 43 (1931) , he used Cepheid variable stars when possible, since he recognized that they were the best of the available distance indicators; but he could measure their properties only in members of the Local Group, such as M31 and M33. For more distant galaxies, Hubble was forced to rely on indicators which he fully recognized were less accurate:
We know now that some of the objects which Hubble considered isolated stars were unresolved blends of star clusters or HII regions. Thus, many of his measurements of distances were underestimates, since he assigned the combined light of many stars to that of a single star.
Now, as for the second part of the required dataset -- radial velocities -- Hubble relied in large part on the work done by Milton Humason, who rose from the position of mule driver and janitor to become one of the best observational astronomers of his day. Many of the crucial spectra were taken with the 100-inch (2.5 meter) telescope at Mount Wilson. As an example, consider the spectrum of NGC 7619. Humason took two photographs:

Taken from
Humason, Contributions from the Mount Wilson Observatory, 3, 21 (1928)
Q: If a typical night is 8 hours long, how can one expose a photographic
plate for 33 or 45 hours?
Based on the two spectra, Humason estimated the velocity of NGC 7619 to be 3828 and 3754 km/s; he found a weighted average of 3779 +/- 100 km/s.
Below are samples of other spectra taken by Humason with the 100-inch telescope and similar equipment.

Figure taken from
Humason, ApJ 74, 35 (1931)
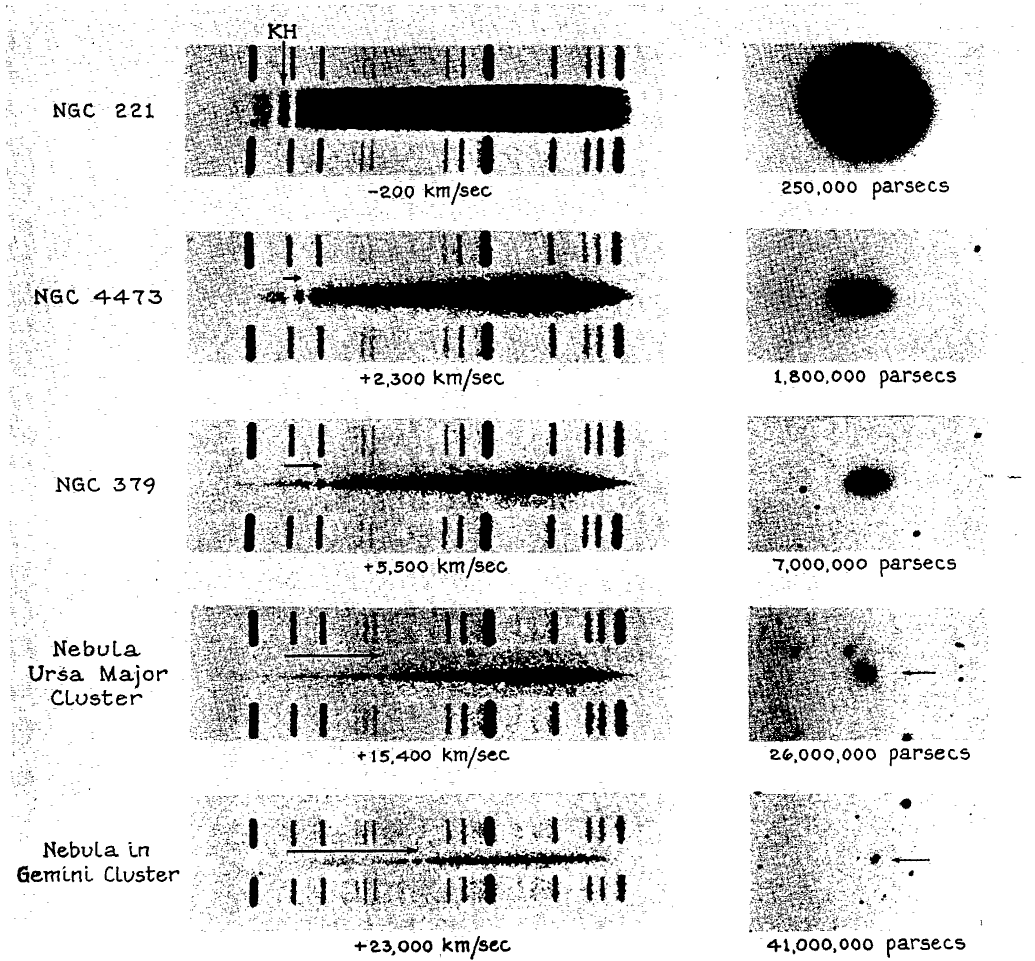
Figure taken from
Humason, ApJ 83, 10 (1936)
Astronomers in recent years have also measured the velocity of NGC 7619. For example, Wegner et al., AJ 126, 2268 (2003) used a telescope of similar size, the MDM 2.4 m at Kitt Peak, to acquire a spectrum with roughly the same dispersion, about 140 Angstroms per mm. However, the modern spectrum
So, give it a try: use the original Hubble diagram (published in 1929) to measure the relationship between velocity and distance. Measure the slope on the graph, and use it to compute the Hubble constant. Warning: the units on the y-axis aren't labelled properly. They should be "km/sec", not just "km."
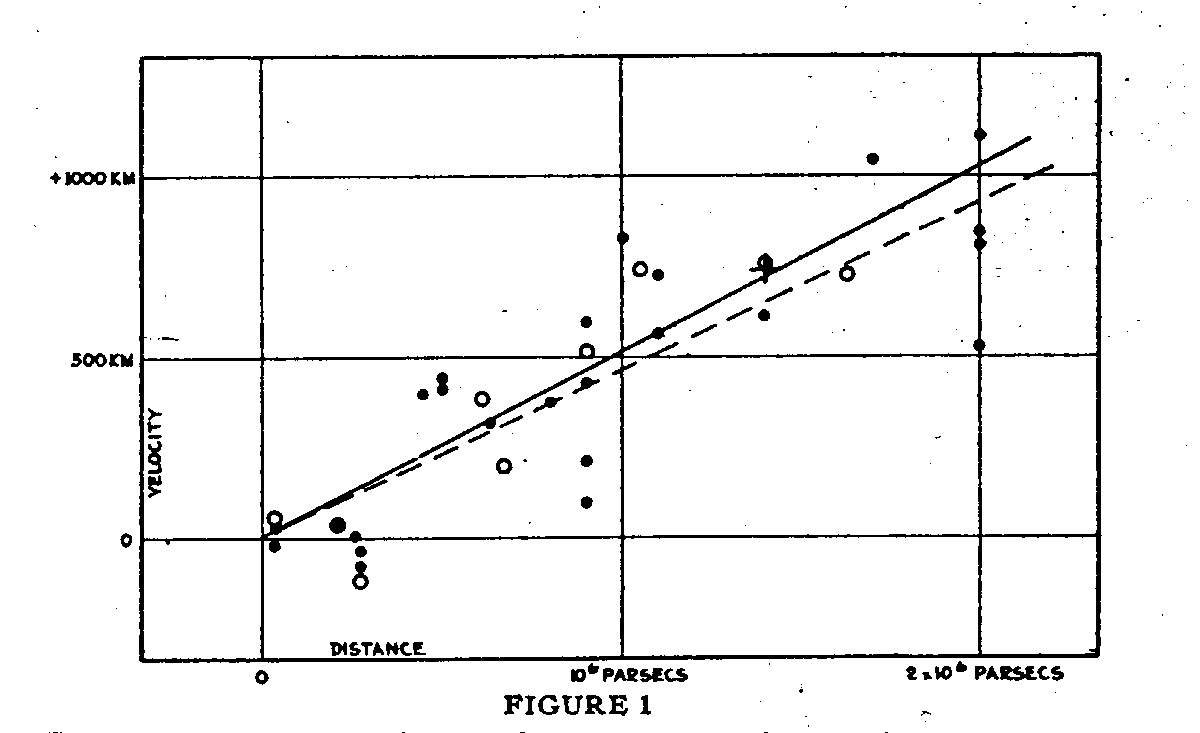
Figure taken from
Hubble, PNAS 15, 168 (1929)
Q: What is the value of the slope on this graph? Convert your
answer to have units of (km/sec) per Mpc.
Okay, fine: so there's a linear relationship between the distance to a galaxy and its recession velocity. What does any of that have to do with expansion?
Mathematically, this behavior can be described by breaking the ordinary concept of "distance" into two pieces:
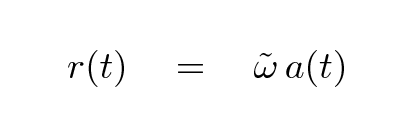
The radial velocity of an object is simply the time derivative of its distance from us,
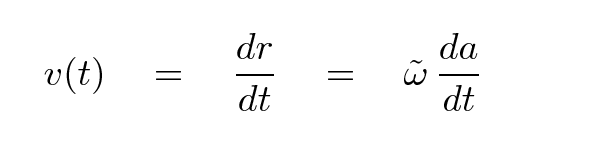
Now, an observational astronomer like Hubble might choose to describe the radial velocity of a galaxy in a different mathematical manner, like this:
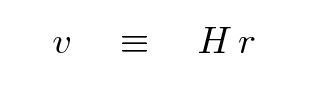
Q: Combine these two ways of describing velocity
to find an expression for the Hubble constant
H in terms of the scale factor a(t).
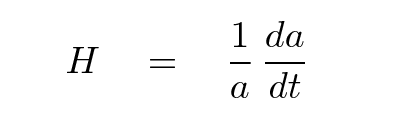
Take another look at the value of the Hubble constant:
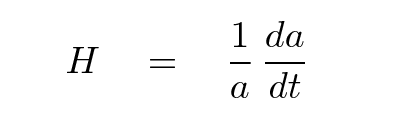
If we take the reciprocal of this expression, we end up with

This quantity has the units of a SIZE divided by a SPEED. It's similar to the expression for "100 miles to Buffalo" divided by "50 miles per hour". The result of that analogy, of course, is a time: "2 hours to reach Buffalo".
In the astronomical version, the expression is also a time: one that we can interpret as the age of the universe (the time taken to reach its current size). If we pretend that the expansion of the universe has been constant, which will turn out not to be a terrible assumption, then we can compute the age of the universe simply by taking the reciprocal of the Hubble constant.
Q: Adopt a value of H = 70 km/sec/Mpc.
Convert the value of H to units of 1/seconds.
What is it in those units?
What is the age of the universe based on this
value of H?
Back in the nineteen-thirties, this putative age of the universe was ... problematic. Geologists estimated that the Earth was at least 3 or 4 billion years old, for example.
We now rely on other means to measure distances to nearby galaxies: in addition to Cepheids -- which we can detect in much more distant galaxies than Hubble could -- we use SBF, PNLF, TRGB, GCLF. Below is a graph showing the distances measured using the SBF technique (Tonry et al., ApJ 475, 399, 1997) to a set of galaxies which is similar to that used by Hubble. The velocities are very similar, but the distances are not.

Q: What is the value of the slope on this graph? Convert your
answer to have units of (km/sec) per Mpc.
Q: How does this value compare to the one based on Hubble's data?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.