How much thermal energy is stored inside a star?

This project must be done by individuals. It must be submitted via myCourses by 5 PM on Dec 1, 2020.

The STATSTAR program creates an output file which lists the properties of a large number of thin shells of material inside a star. Let's use some of those tabulated values to compute the total "thermal energy" of the gas inside a Sun-like star.

By "thermal energy", I mean "the kinetic energy of all the particles in the gas." As you may recall, the thermal energy of particles in a gas depends solely on the temperature of the gas:

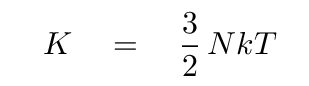
So, if you can figure out the number of particles N in a shell of the model, and the temperature of the gas in that shell, then you can compute the thermal energy of that shell. Add up the thermal energy of all the shells in the star, and voila! you have the total thermal energy.

There are two tricky bits to this project.

1. What is the number of particles in each shell? The STATSTAR output provides the density of the shell and the radius of the shell. You can compute the volume of each thin shell using its radius, and the radius of the previous shell. So, it's easy to compute the mass inside each shell.

   But in order to figure out the number of particles, you need to do some extra work. We will make the following assumptions:

   • mass fraction of hydrogen X = 0.70
   • mass fraction of helium Y = 0.292
   • mass fraction of everything else Z = 0.008
   • the "typical" heavy atom is Oxygen -- so, assume all the "Z" atoms are oxygen
   • all the atoms, of all types, are completely ionized

   As a warmup, please work out the following, step by step, and include it with your project. Consider 1 kg of gas with the above composition.

   1. how many hydrogen atoms are there?
   2. how many particles (electrons plus nuclei) due to completely ionized hydrogen atoms are there?
   3. how many helium atoms are there?
   4. how many particles (electrons plus nuclei) due to completely ionized helium atoms are there?
   5. how many oxygen atoms are there?
   6. how many particles (electrons plus nuclei) due to completely ionized oxygen atoms are there?
   7. how many total particles (electrons plus nuclei) are there in this kg?

   Good. You have just calculated the number of particles inside every kg of ionized gas in the star. That means that you can convert the MASS of each shell into the total number of particles N of each shell.

2. In order to compute the mass of each shell, in kg, you need to read data from the STATSTAR output file. In this file, the important columns are:
   • column 1: the outer radius of each shell, in cm. You should convert from cm to meters for your calculations.
   • column 4: the temperature of each shell, in Kelvin.
   • column 6: the density of each shell, in grams per cubic cm. You should convert into units of kg per cubic meter for your calculations.

Here's the datafile you should use. It's the result of running STATSTAR on a star of 1 solar mass, with the chemical composition given above, and an effective temperature of 5500.2 Kelvin. There are two versions with the same numbers -- use whichever one is easier for you to read into a program.

• STATSTAR output file starmod.dat (spaces between columns)
• STATSTAR output file starmod.csv (commas between columns)

Your task is to compute the following quantities:

1. add up the mass of each shell to compute the total mass of the stellar model. It SHOULD be very close to the mass of the Sun. If your value isn't close to this mass, there may be something wrong with your analysis of the datafile (perhaps you didn't convert into MKS units ...). You may find that your value is just a few percent smaller than the total mass of the Sun; that's okay. Can you explain why it might be just a bit smaller?

   Write down this total mass.

2. for each shell, compute the number of particles in the shell, and use that plus the temperature to compute the thermal energy of the shell, in Joules. Add up the energy of all the shells to yield the total thermal energy of the star, in Joules. Write down this energy.
3. compare this total thermal energy to the luminosity of the star, which is

   
                L = 0.86071 Lsolar = 3.27 x 1026 J/s
       

   If an evil wizard waved his staff and caused all fusion in the star's core to stop, how long could the star continue to radiate the same luminosity, if it used up all the thermal energy stored in the gas? Could this stored thermal energy power the star for the actual age of the solar system?

Scan/photograph all your work, which must include the "warmup" exercise, as well as the answers to items A, B, C. Create a single PDF file with all the material, and submit it via myCourses.

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.