The center of mass of a pyramid

Image courtesy of Brian Chu and Ecogarden

A pyramid has a square base, each side of length L. It has a height H. Where is the center of mass of the pyramid?

Well, it's obvious from symmetry that it must lie somewhere along a vertical line which drops down from the top of the structure. But how far below the top (or how far above the bottom)?

We can solve this problem by breaking the pyramid up into a set of similar shapes: flat, thin squares. We'll imagine that the pyramid is made up of stone which has a density ρ kg per cubic meter.

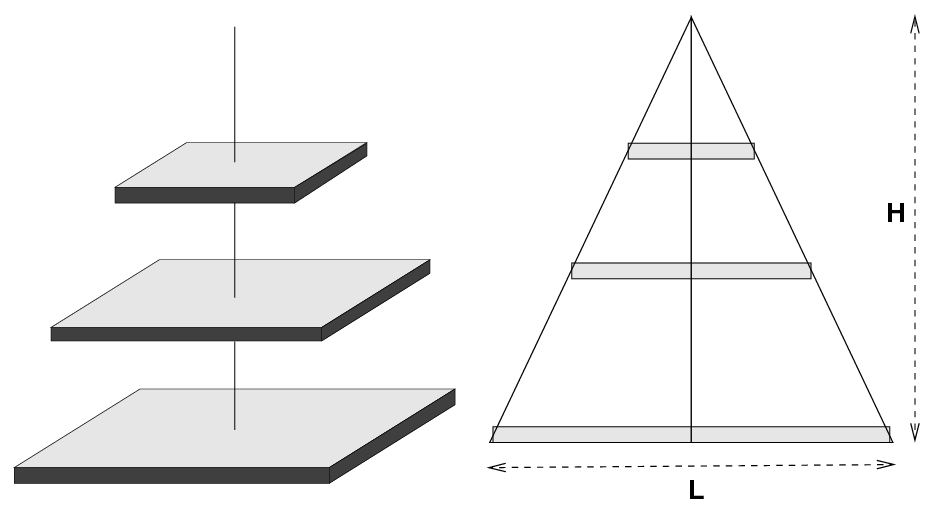
Consider just ONE of these squares, at some distance h above the base. Give this square a thickness dh, some extra little height.

1. What is the length and width of this thin square slab? Express it in terms of h, L and H.
2. What is the volume of this thin square slab?
3. What is the mass of this thin square slab?

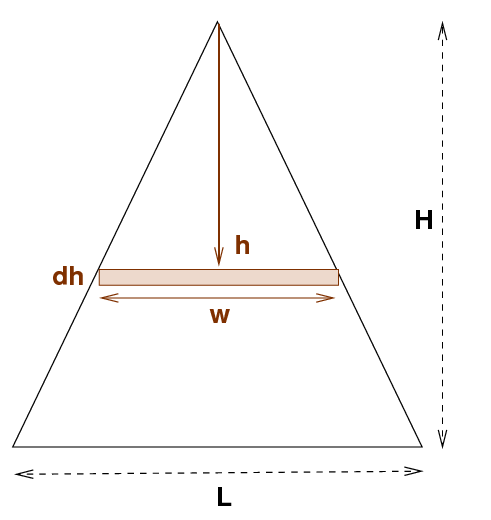
To find the total mass of the structure, you need to add up the masses of all the little slabs which run from the bottom of the pyramid -- h = 0 -- to the top of the pyramid -- h = H.

To find the center of mass of the structure, you need to add up a similar set of values ... but this time you need to multiply the mass of each little slab by the height h of that slab above the base.

So, where is the center of mass of the pyramid?

Let's make it concrete (ha ha!). The pyramid of Khufu has ρ = 2700 kg per cubic meter, L = 240 m and H = 153 m.

1. What is the mass of the pyramid?
2. How far above the base is the center of mass of this pyramid?

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.