A more complicated energy problem

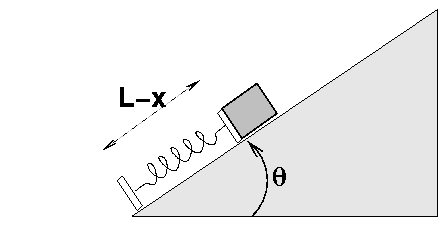
Just as before, an ideal spring of rest length L = 2 m and spring constant k = 120 N/m is placed on a ramp of angle theta = 20 degrees. This time, however, the ramp is not frictionless; instead, it has coefficient of kinetic friction mu_k = 0.07 . You then gently place a block of mass m = 1.5 kg onto the ramp and glue it onto the end of the spring. You push the block down until it compresses the spring by a distance x = 0.2000 m. You can feel the spring pushing back up against the block, so you have to hold the block in place.

At this moment, what is the total energy of the spring-and-block system? State clearly your choice of zero for all potential energies.
You now release the block, and it starts to slide up the ramp.
What is the speed of the block when the spring returns to its rest length?
As the block continues to slide up the ramp, it pulls the spring with it; the spring is now stretched beyond its rest length. What is the speed of the block when it reaches a distance x2 = 0.0412 m beyond the spring's rest length?
How far beyond its rest length will the spring stretch until the block comes to a momentary halt (and then slides back down)?