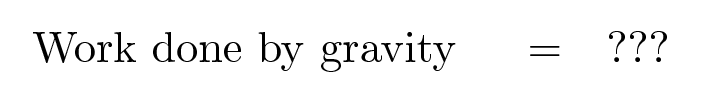
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
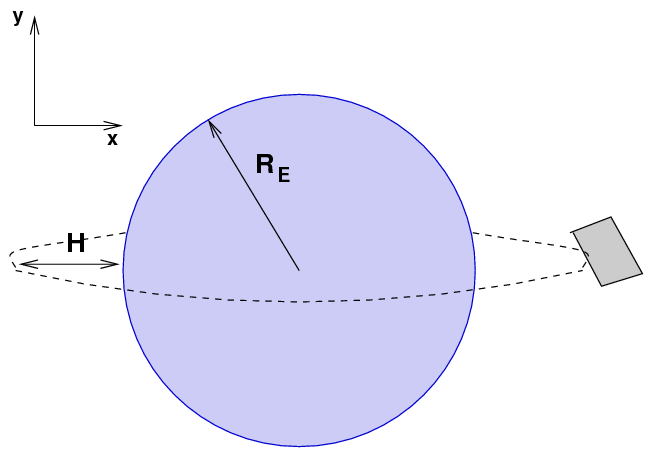
Suppose that you want to put an object in orbit around the Earth --- at roughly the same altitude as the International Space Station, or many other satellites. We'll use an altitude of H = 400 km for this example.
For simplicity, let's pick a simple, small object: a textbook with a mass of m = 1 kg..
The first thing to do is to compute the work done by gravity on the textbook as it moves from the surface of the Earth to the height H.
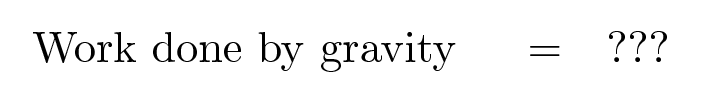
How much work must our rocket perform on the book in order to raise the book against the pull of gravity?
Now, suppose that we do manage to raise the book from the surface of the Earth to the desired height H. What will happen when we open the rocket's payload bay and release the book?
AAaaaaaaaaaa......... *thump*
Hmmmm. Apparently, simply raising the book up above the surface isn't enough. We also need to give the book enough speed that it circles the Earth in a stable orbit.
Which is larger?
Work to raise book to orbit =
Work to give book orbital velocity =
So, we know much energy it takes to raise the book to orbital height, and then give it orbital velocity. How much should it cost?
Suppose we could use an electric motor and a really, really long extension cord. The cost of electrical energy from RG&E is pretty low:
1 kilowatt-hour = $ 0.10
Does this look ... fishy to you?
There are several companies which will put an object into orbit for you, using rockets. One of them is SpaceX , which was founded by Elon Musk, who made his fortune in an Internet startup company.
SpaceX has several models of rocket. Let's look at the Falcon-9.
Golly, that's a LOT more expensive.
Well, one of the things we haven't taken into account is the air resistance on the rocket as it makes its way into orbit. To a very rough approximation, we can compute the air resistance on the rocket with a formula like this:
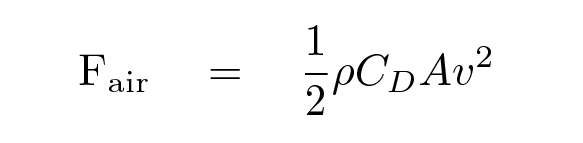
We'll simplify again, but it will give us a good idea for the order of magnitude. Let's use the following values:
ρ =
CD =
A =
v = 100 m/s
Note that the air resistance force goes up sharply as one approaches and crosses the speed of sound ...

.... so the real force of air resistance will be even greater than we have calculated.
What sort of work does air resistance do on the rocket? Why?
But the major reason that it costs SO MUCH to put even a small payload into orbit is because one has to carry much of the fuel along for the ride. If you want to put a 1-kg textbook into space, you have to use a pretty big machine to do it. The walls and motors and especially the fuel have to go up into the air, too, greatly increasing the amount of stuff you are lifting off the ground.
For example, consider the Falcon-9 again.
This is the reason that travel to orbit is so expensive. In just a few weeks, we'll take a more quantitative look at the ratio of payload to fuel when we talk about momentum and rockets.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.