 Viewgraph 1
Viewgraph 1
 Viewgraph 2
Viewgraph 2
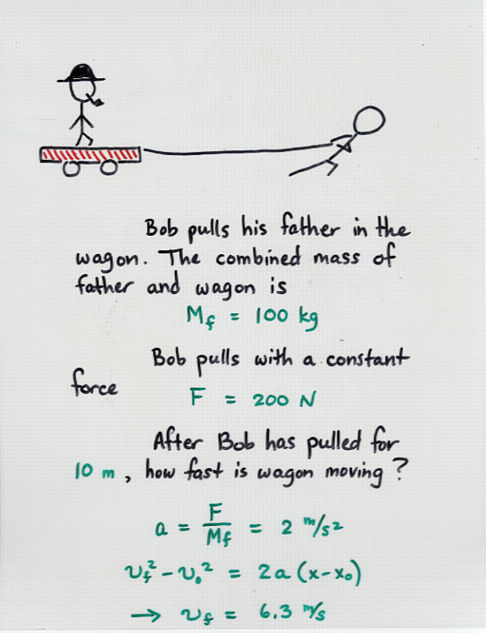 Viewgraph 3
Viewgraph 3
 Viewgraph 4
Viewgraph 4
 Viewgraph 5
Viewgraph 5
 Viewgraph 6
Viewgraph 6
 Viewgraph 7
Viewgraph 7
 Viewgraph 8
Viewgraph 8
 Viewgraph 9
Viewgraph 9
 Viewgraph 10
Viewgraph 10
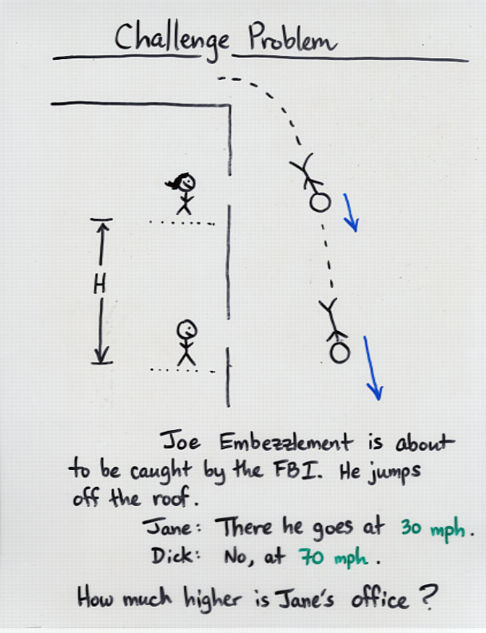 Viewgraph 11
Viewgraph 11
 Viewgraph 12
Viewgraph 12
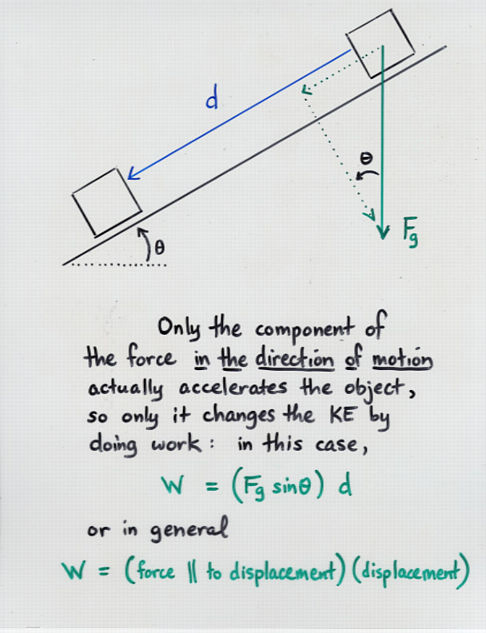 Viewgraph 13
Viewgraph 13
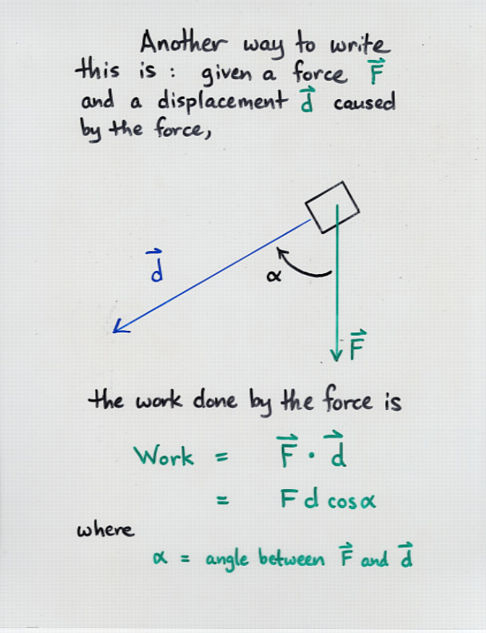 Viewgraph 14
Viewgraph 14
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
2
KE = 1/2 * m * v
KE(final) - KE(initial) = (force) (distance)
where the force is applied over some distance.
KE(final) - KE(initial) = Work done on object
KE(final) - KE(initial) = (force parallel to displacement) (distance)
KE(final) - KE(initial) = F (dot product) d
= F * d * cos(alpha)
where alpha is the angle between vector F and
vector d.
Viewgraphs
 Viewgraph 1
Viewgraph 1
 Viewgraph 2
Viewgraph 2
 Viewgraph 3
Viewgraph 3
 Viewgraph 4
Viewgraph 4
 Viewgraph 5
Viewgraph 5
 Viewgraph 6
Viewgraph 6
 Viewgraph 7
Viewgraph 7
 Viewgraph 8
Viewgraph 8
 Viewgraph 9
Viewgraph 9
 Viewgraph 10
Viewgraph 10
 Viewgraph 11
Viewgraph 11
 Viewgraph 12
Viewgraph 12
 Viewgraph 13
Viewgraph 13
 Viewgraph 14
Viewgraph 14
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.