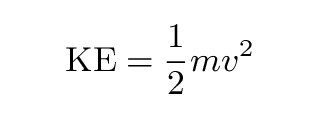
Let's start out with a simple problem that you should be able to solve. It involves a boy sliding on a sidewalk ...
Uh-oh. If the forces change during motion, so that the acceleration changes, we may not be able to apply the good old kinematic equations. What can we do then?
Sometimes (but not always), we can use a certain combination of force and distance to determine the work performed on an object as it moves. Work is a measure the kinetic energy it gains or loses. You remember kinetic energy, right?
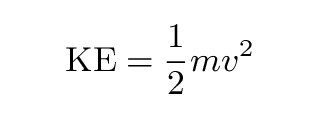
The work done on some moving object by a single force is the integral of the force along the path:
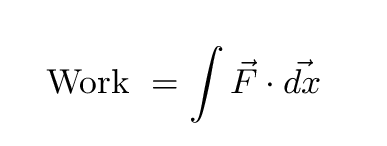
This integral involves a dot product. We'll deal with this combination of vectors in more detail next time; for now, just remember
For a one-dimensional force, the work is the area "under" the curve of F versus x.
If there are several forces acting at once, we need to compute the net work, which is the integral of the net force.
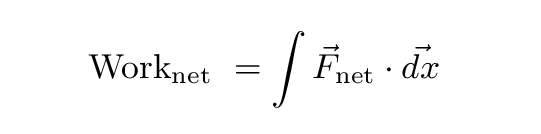
Once we know the net work done on an object as it moves, we can use the "Work-Kinetic Energy Theorem" to figure out how much its speed has changed:
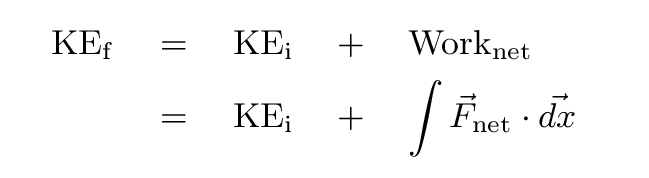
Now that you know all that, let's try those icy sidewalks again ....