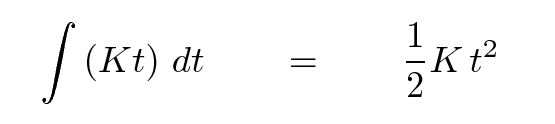Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The notion of integration -- Part II
What is integration? The basic idea is pretty simple:
Integration is the act of adding up a bunch of little
actions
That's really all there is to it. The procedure of performing
this addition may at times involve a number of steps,
but when we integrate, all we're doing is adding together
a bunch of little pieces.
Bob the Banker rakes in the bucks
Bob works at Soldman Gachs, the giant investment bank.
He works on commission -- the more clients he finds,
the more money he makes.
Bob is paid $10,000 per month for each client he maintains.
Bob starts off in January with just one client.
During that month, he gets in touch with another,
so when February starts, he has two clients.
During the Presidents' Day Parade, he chats with
an industrialist ... so when March rolls around,
he has three clients.
In fact, Bob manages to add one more client to his Rolodex
every month.
January 1 client
February 2 clients
March 3 clients
April 4 clients
May 5 clients
June 6 clients
July 7 clients
August 8 clients
September 9 clients
October 10 clients
November 11 clients
December 12 clients
How much does Joe make over the course of one year?
-
One way to solve this problem is to add up his
wages for each month.
-
total over 12 months = ($10,000/client/month) * (1 client) * (1 month)
+ ($10,000/client/month) * (2 clients) * (1 month)
+ ($10,000/client/month) * (3 clients) * (1 month)
+ ($10,000/client/month) * (4 clients) * (1 month)
+ ($10,000/client/month) * (5 clients) * (1 month)
+ ($10,000/client/month) * (6 clients) * (1 month)
+ ($10,000/client/month) * (7 clients) * (1 month)
+ ($10,000/client/month) * (8 clients) * (1 month)
+ ($10,000/client/month) * (10 clients) * (1 month)
+ ($10,000/client/month) * (11 clients) * (1 month)
+ ($10,000/client/month) * (12 clients) * (1 month)
= $ 10,000
+ $ 20,000
+ $ 30,000
+ $ 40,000
+ $ 50,000
+ $ 60,000
+ $ 70,000
+ $ 80,000
+ $ 90,000
+ $100,000
+ $110,000
+ $120,000
= $ 780,000
-
We can also look at this problem graphically.
-
We're adding up wages over time, so let's make a graph
on which the wages go on the vertical axis,
and time goes on the horizontal axis, like this:
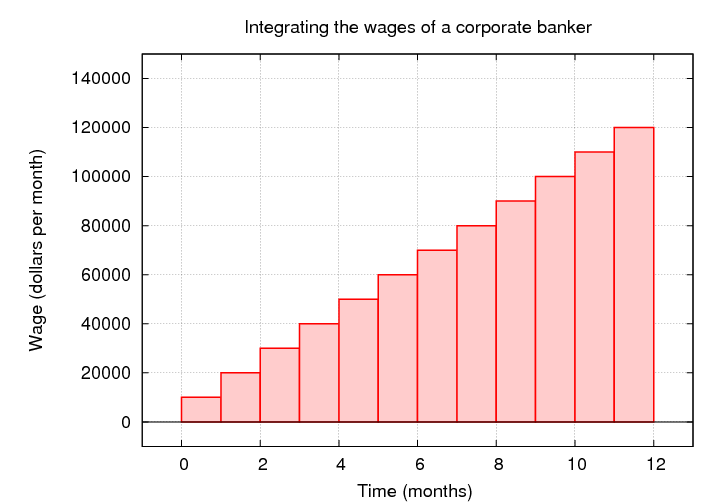
The amount of money Bob makes during the first month is given
by the area of the first red box: $10,000 per month times 1 month = $10,000.
If we add up the area of all the red boxes, we get Joe's total
for the year: $780,000.
Bob's private bank account is growing
On Jan 1, 2010, when Bob starts work at the firm,
his working income account is completely empty. Zero.
(He has some offshore accounts, too, but we're ignoring those for now).
Let's look at Bob's private bank account balance as
the year progresses.
On Jan 1, when Bob starts, his account has $0.
But on Feb 1, after one month, his account is credited with $10,000.
We could make a table showing the bank balance as a function
of time:
Date Bank account balance
--------------------------------------------
Jan 1, 2010 $ 0
Feb 1 $ 10,000
Mar 1 $ 30,000
Apr 1 $ 60,000
May 1 $ 100,000
Jun 1 $ 150,000
Jul 1 $ 210,000
Aug 1 $ 280,000
Sep 1 $ 360,000
Oct 1 $ 450,000
Nov 1 $ 550,000
Dec 1 $ 660,000
Jan 1, 2011 $ 780,000
--------------------------------------------
Hmmmm. That bank account starts off growing slowly,
but it is increasing very rapidly by the end.
That's pretty obvious if we make a graph, showing the
account balance as a function of time.
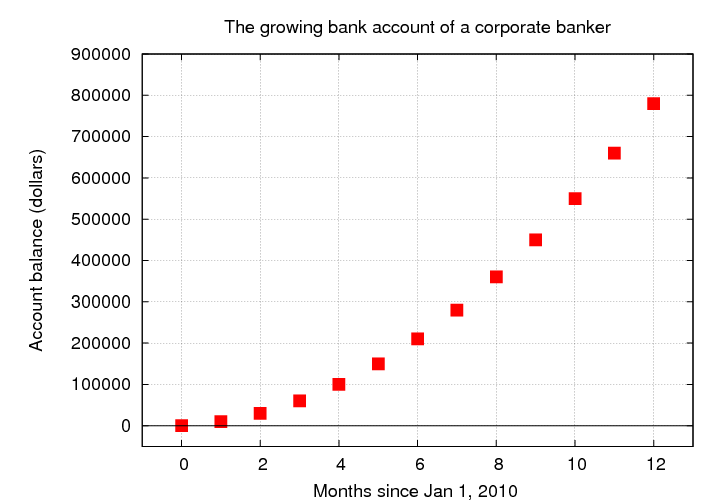
What do we learn from this story?
We can express Bob's experience in ordinary speech:
If your salary goes up over time, then
your total income grows by leaps and bounds.
But we could be a bit more precise:
If you put money into the bank at an increasing rate,
your account balance grows by larger and larger amounts.
If we step back and look at this example through the eyes
of a mathematician, we can describe it precisely using technical
language:
If you integrate a linearly increasing function,
you end up with a quadratically increasing function.
We can even put it into mathematical symbols:
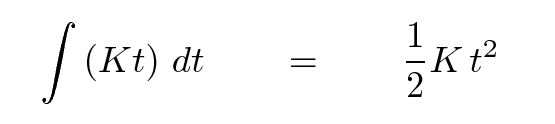
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.