Creative Commons License Copyright © Michael Richmond. This work is licensed under a Creative Commons License.

How to aim a gun

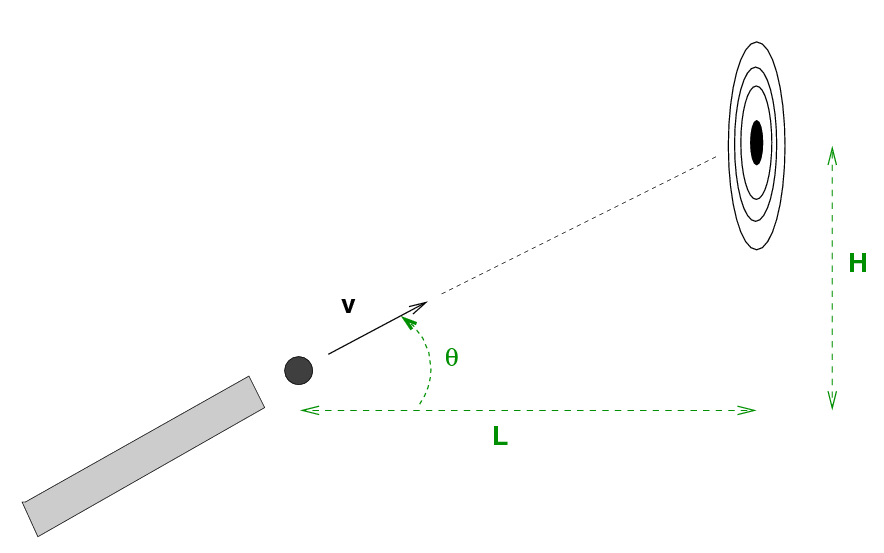
Suppose you want to fire a gun at a target. Should you simply aim the gun so that it points directly at the center of the target?

No, of course not. If you do, the bullet will strike the target slightly below the desired point.

At the front of the room, I've set up a gun and a target. The values for the range and height of the target are: 



     L  =   58.5 cm

     H  =   33.7 cm

  1. What is the line-of-sight angle &theta in this case?

  2. Suppose that we do (foolishly) aim the gun at this angle, so it points straight at the target. The velocity of the gun is 512 cm/s. What will the height of the bullet be when it reaches the horizontal position of the target?

Clearly, you need to aim at some location which is above the center of the target -- in other words, aim at some angle α which is larger than the simple line-of-sight angle θ.

But how can you find this proper angle?

  1. Write down one equation which shows the horizontal position of the bullet x(t) as a function of time. Use the symbol &alpha to denote the unknown angle of the gun.

  2. Write down a second equation which shows the vertical position of the bullet y(t) as a function of time. Use the symbol &alpha to denote the unknown angle of the gun.

  3. How many unknown quantities are there in these 2 equations?

  4. Can you think of a method to find the proper angle?

Creative Commons License Copyright © Michael Richmond. This work is licensed under a Creative Commons License.