Connections between velocity and acceleration

Position tells you the location of an object.

Velocity tells you how fast is the position is changing.

Acceleration tells you how fast is the velocity is changing.

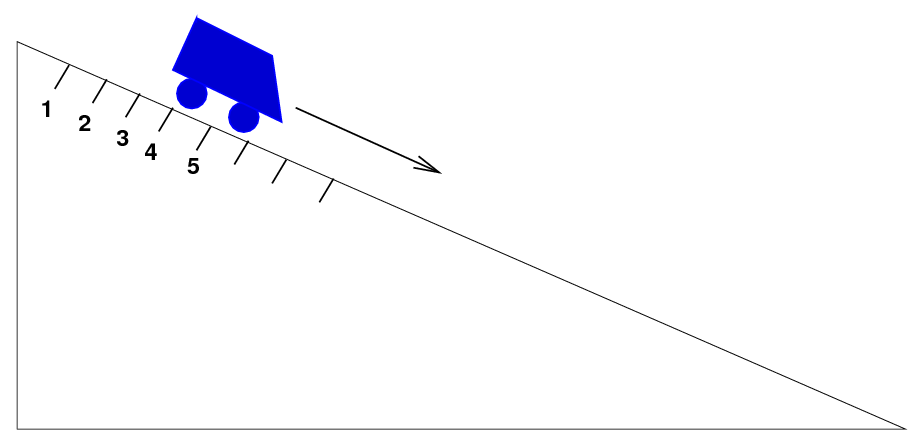
For example, let's put a little toy car on a tilted ramp and let it roll downwards. We'll measure the position x of the car from the top of the ramp.

time	0 s	1 s	2 s	3 s	4 s
car's position	0 m	0.3 m	1.2 m	2.7 m	4.8 m



  Q:  What is the average velocity between times t = 0 and t = 1 ?

  Q:  What is the average velocity between times t = 1 and t = 2 ?

  Q:  What is the average velocity between times t = 2 and t = 3 ?

  Q:  What is the average velocity between times t = 3 and t = 4 ?


  Q:  Are these velocities all the same?

But suppose we look at the CHANGES in velocity ....

time	0 s - 1 s	1 s - 2 s	2 s - 3 s	3 s - 4 s
avg velocity	0.3 m/s	0.9 m/s	1.5 m/s	2.1 m/s



  Q:  What is the change in average velocity between the first
            two measurements?

  Q:  What is the change in average velocity between the second
            two measurements?

  Q:  What is the change in average velocity between the third
            two measurements?


  Q:  Are these CHANGES in velocities all the same?

Physicists call the change in velocity with respect to time acceleration.

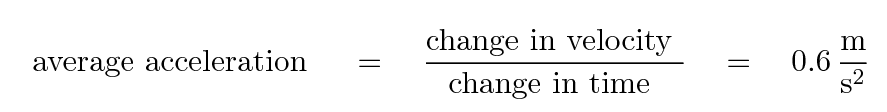
Note the units: meters per second per second, or meters per second squared.

If you measure the velocity at several times and look at the change in its value, you can calculate the average acceleration, just as we did above. But if someone gives you an equation for velocity as a function of time .....

time	1.5 s	2.5 s	3.5 s	4.5 s
avg velocity	0.3 m/s	0.9 m/s	1.5 m/s	2.1 m/s



   Q:  Write an equation for velocity as a function of time,
           based on the measurements of the toy car.


             v(t)  =   ___________   +  _____________

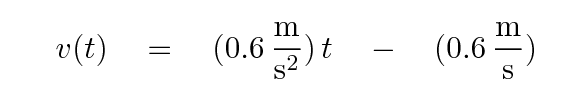
The instantaneous acceleration is just the derivative of the velocity with respect to time.



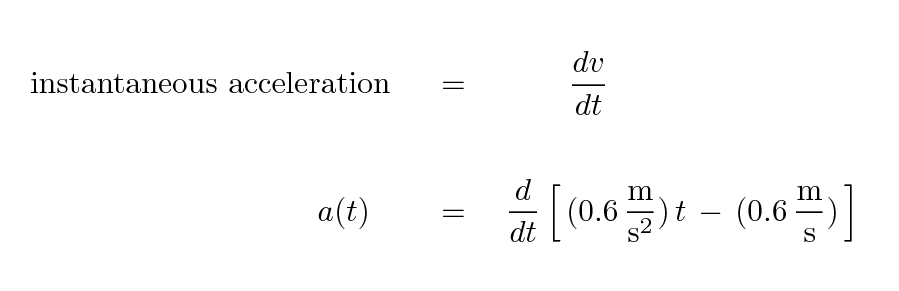
  Q:  What is the acceleration of the toy car?

Let's look at the motion of this toy car using graphs. If we plot position as a function of time, we see a curve instead of a straight line. This curve tells us that the car is not travelling with a constant velocity.

Since the derivative of position with respect to time is velocity, we can find the velocity at some moment by measuring the slope on this graph. For example, to find the velocity at time t = 1.5 seconds,

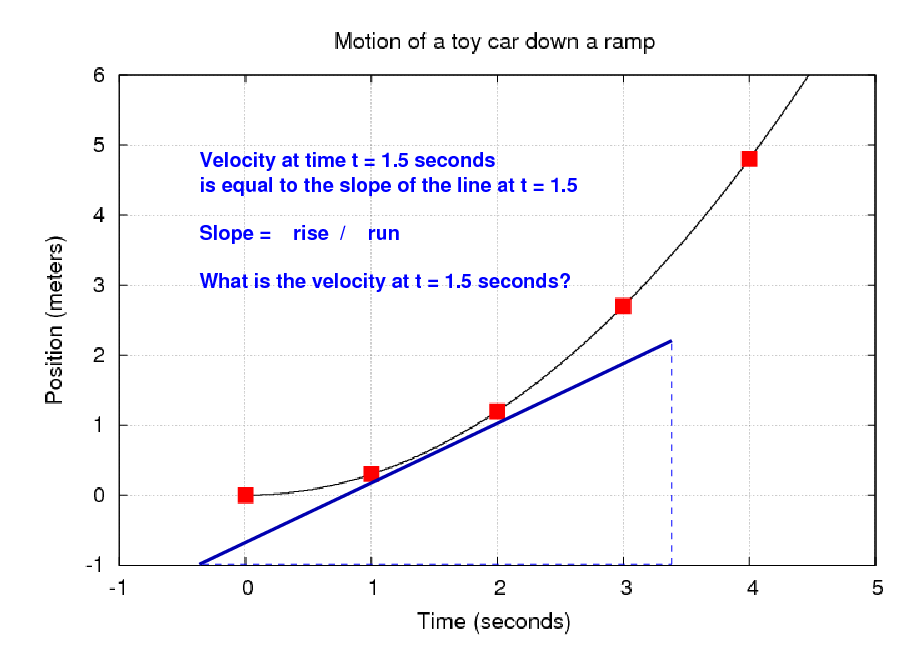
If we plot velocity as a function of time instead, then we do see a straight line.

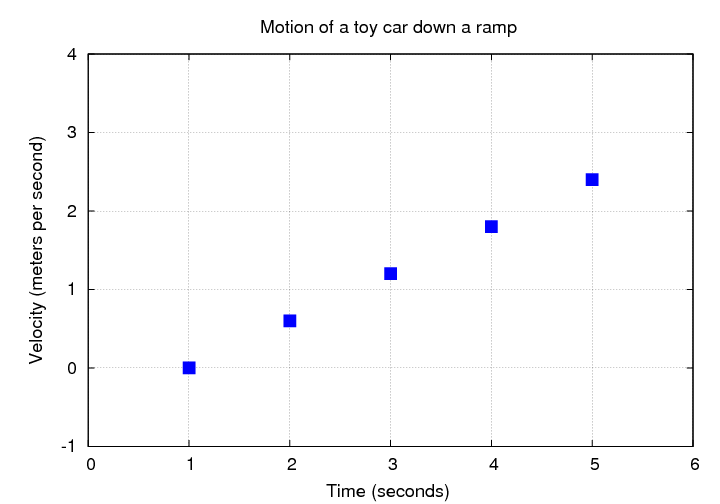
Since acceleration is the derivative of velocity with respect to time, we can determine the acceleration of the car by measuring the slope on this graph.



  Q:  What is the acceleration of the toy car down the ramp?

So far, we've started with position or velocity, taken derivatives, and used them to determine acceleration. But we can go the other way as well: if someone gives us the acceleration of an object, we can integrate to find the velocity.

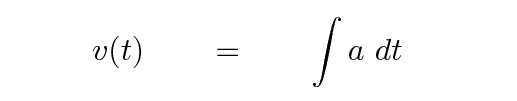
Remember -- every time you integrate, you must check your information in order to figure out the appropriate constant to add to the answer.

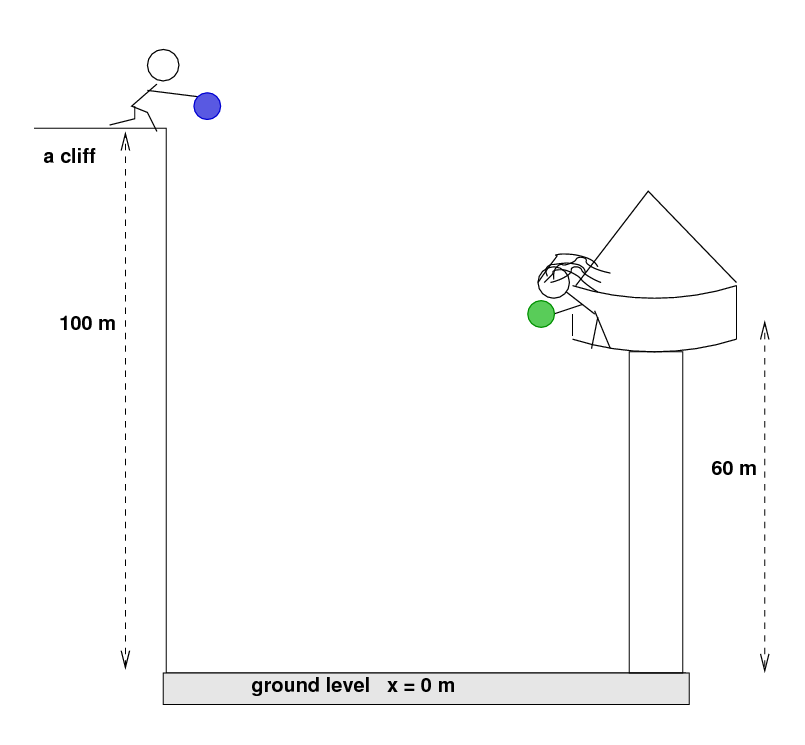
Rapunzel drops a green ball from her tower at t = 0 s. The Prince drops a blue ball from his cliff at t = 0 s. Each measures the motion of his ball as it falls. Both Rapunzel and the Prince measure an acceleration of

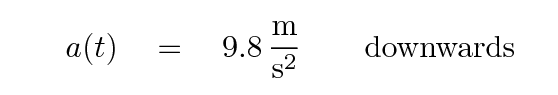
The two lovers decide to measure positions x starting at the ground, where x = 0. They decide that the position will increase going upwards, so Rapunzel is at x = 60 m and The Prince is at x = 100 m. Since x increases going up, but the acceleration is directed downwards, they must write

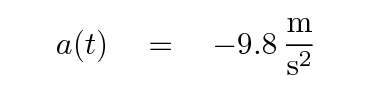
Now, can you start with this acceleration and figure out the velocity of the Prince's ball, or Rapunzel's ball?



  Q:  Integrate the acceleration of The Prince's ball 
            with respect to time to find the velocity.  
            Write an equation

 
             blue ball  v    (t)  =   _________   +  ____________
                         blue



  Q:  Integrate the acceleration of Rapunzel's ball 
            with respect to time to find the velocity.  
            Write an equation

 
            green ball  v     (t)  =   _________   +  ____________
                         green



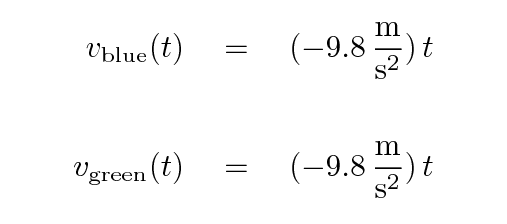
  Q:  Do the two balls have identical equations for velocity 
               as a function of time?

You can check that your velocity is correct: take the derivative with respect to time. Do you end up with the correct acceleration?



   Q:   Take the derivative of the blue ball's velocity to find its
                  acceleration.


   Q:   Take the derivative of the green ball's velocity to find its
                  acceleration.

Okay, good. Now let's integrate again, starting with velocity, to find an equation for the position as a function of time for each ball.



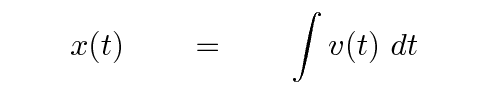
  Q:  Integrate the velocity of The Prince's blue ball 
            with respect to time to find the velocity.  
            Write an equation

 
        blue ball  x    (t)  =   _________   +  ____________  
                    blue



  Q:  Integrate the acceleration of Rapunzel's green ball 
            with respect to time to find the velocity.  
            Write an equation

 
       green ball  x     (t)  =   _________   +  ____________  
                    green

If you have time ....

Make a graph which shows position as a function of time: position on the vertical axis, time on the horizontal axis. Your graph should run from times t = 0 to t = 5 seconds, and from position x = 0 to x = 120 meters.
On the graph, plot the position of the Prince's blue ball using little crosses. Place marks at t = 0.0, 0.5, 1.0, 1.5, etc.
On the graph, plot the position of Rapunzel's green ball using little circles. Place marks at t = 0.0, 0.5, 1.0, 1.5, etc.
Use your graph to estimate the velocity of each ball at t = 1.5 s and at t = 3 s.