 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Position simply tells you the location of an object.
What are the proper SI units to use for measurements of position?
meters (m)
Scientists often use the letters x and y to denote the position of an object. We'll deal with one-dimensional motion this week, so we'll usually stick with x; but when we reach two-dimensional motion, we'll use y, too. In three dimensions, of course, we could use x, y, and z.
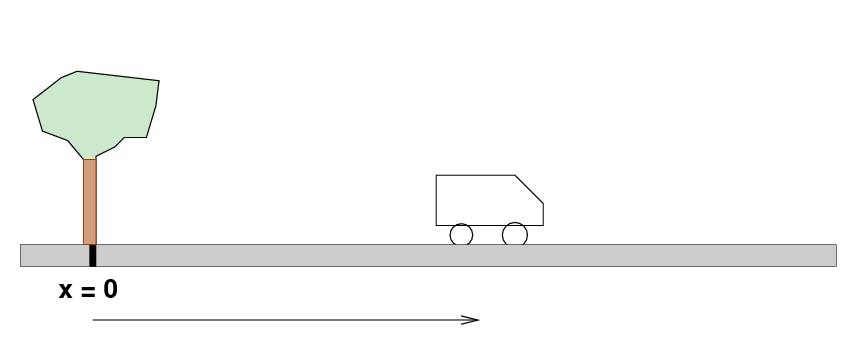
Example: a car drives along a street past a tree.

We measure the position of the car at various times. There are (at least) three ways to communicate our measurements to someone. One is to make a table of the results:
| time | 0 s | 1 s | 2 s | 3 s | 4 s |
| position | 30 m | 35 m | 40 m | 45 m | 50 m |
Another way to describe the motion is to make a graph. We'll be doing this a lot.

A third way to describe motion is by writing a mathematical equation which shows the position x as a function of time t. How can we do that? Well, let's look at how the position changes over time. For example, between t = 0 s and t = 1 s , we see
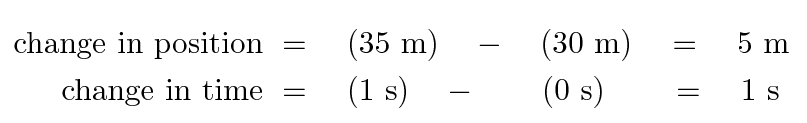
So, the ratio of "change in position" to "change in time" is
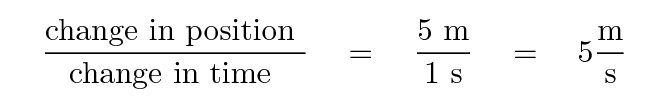
Physicists call this quantity average velocity. It clearly must have the units of meters per second. In this case, we see that
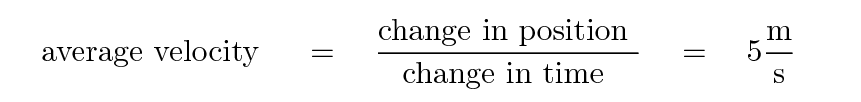
Okay, your turn.
Q: What is the average velocity of the car from t = 2 s to t = 4 s?
Right. It's still v = 5 m/s. In fact, as far as our measurements go, the car has a constant velocity. We can write an equation describing its position as a function of time in this simple case like so, right?
| time | 0 s | 1 s | 2 s | 3 s | 4 s |
| position | 30 m | 35 m | 40 m | 45 m | 50 m |
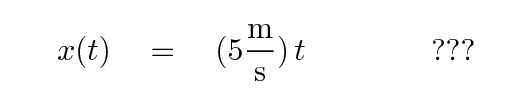
No, that won't work. In order to force the equation to match the measurements, we need to add a constant distance.
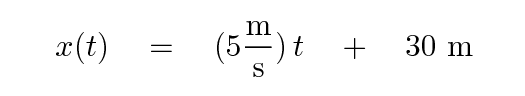
Check this -- do all the terms end up with the same units? What are those units?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.