The New Horizons mission

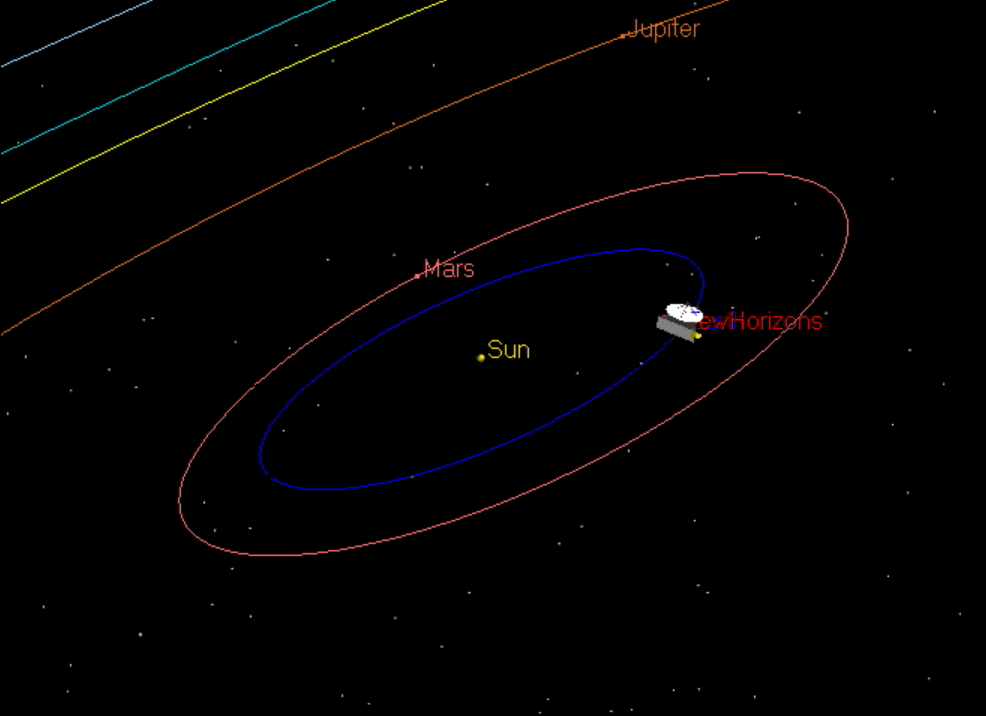
On January 19, 2006, the New Horizons spacecraft was launched from Earth. Its goal -- to reach Pluto and send back images and other data from that distance body.

About 13 months later, the spacecraft approached Jupiter.

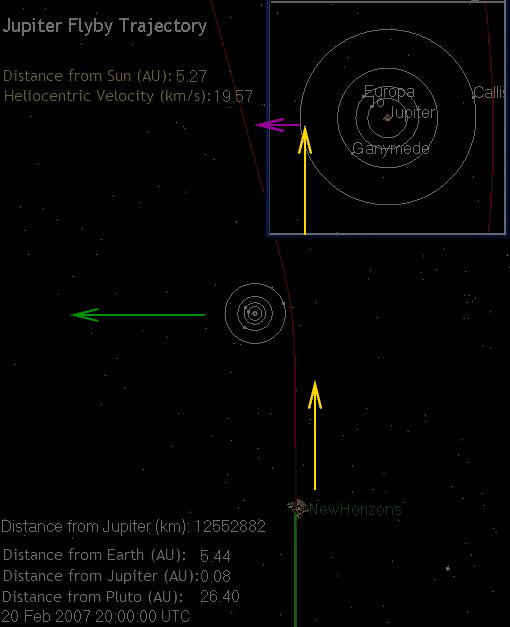
If we look at the trajectory of the spacecraft after it passed Jupiter, we see quite a strong bend:

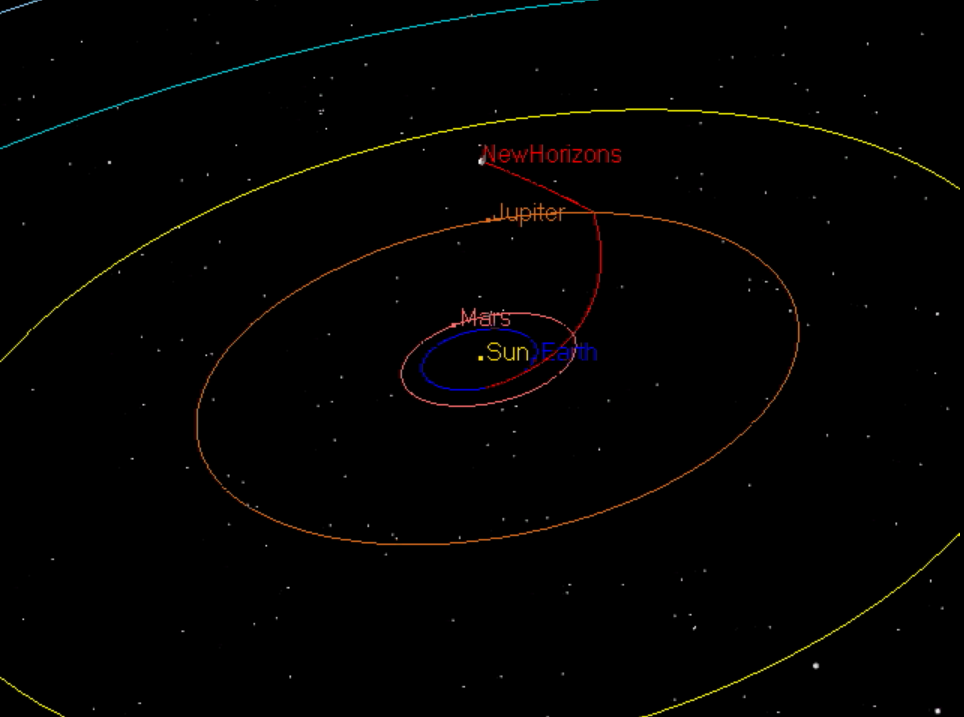
This surely adds lots of extra distance to the journey of the New Horizons spacecraft. Why didn't it simply take a direct path, straight from the Earth to Pluto?

To answer that question, let's compare one aspect of the direct path to that of the actual path.

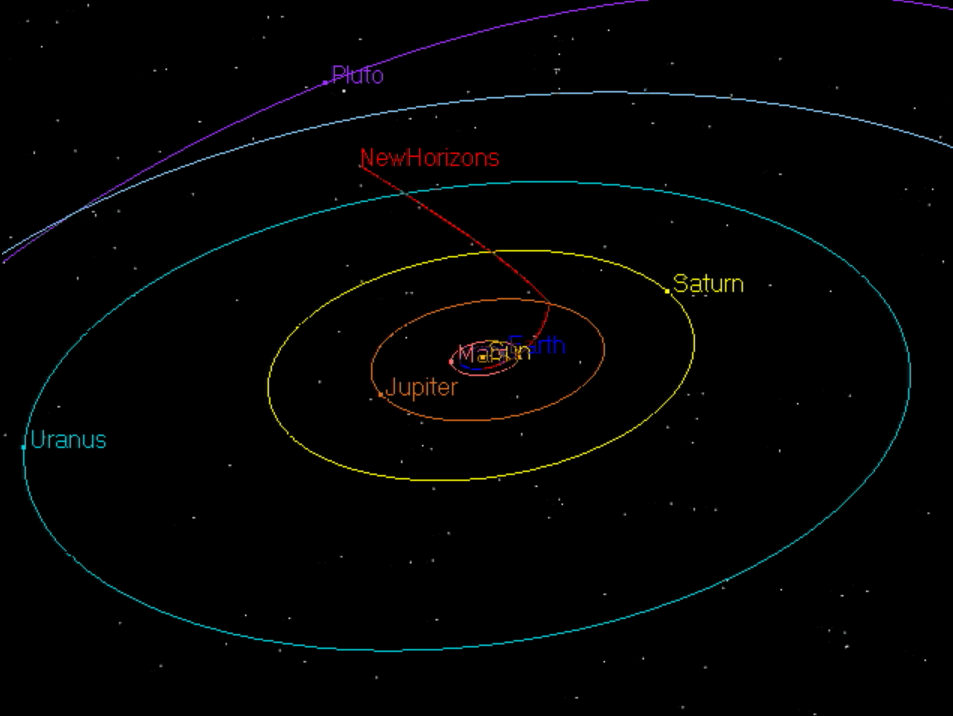
How fast will the spacecraft be moving when it reaches Pluto?

Let's look at two moments in the journey to Pluto:



G                        6.67 x 10^(-11)  N*kg^2/m^2
Mass of Sun:             1.99 x 10^(31)   kg
Mass of New Horizons     4.8  x 10^(2)    kg


                      Just before Jupiter             Flying past Pluto
----------------------------------------------------------------------------

Dist from Sun            8.43 x 10^(11)                 4.91 x 10^(12)
 (m)


Speed rel to Sun         19,580       
 (m/s)


          G M m
 GPE = - --------
            R


          1     2
  KE = + --- m v
          2


total Energy

----------------------------------------------------------------------------

Your job: figure out the speed the spacecraft would have at Pluto if it took the direct route.

Compute the GPE of the spacecraft at each location
Compute the KE of the spacecraft just before Jupiter
Compute the total energy of the spacecraft just before Jupiter
Figure out the KE of the spacecraft at Pluto

So, if New Horizons took the direct route, how fast would be going when it reached Pluto?

Now, if we actually look at the mission plan, it turns out that the New Horizons spacecraft will be travelling much faster when it passes Pluto and Charon: v = 13,800 m/s. How can that be?

will the spacecraft use its engines? NO
perhaps energy isn't conserved? YES, IT IS CONSERVED

Then how can it pick up this extra speed and kinetic energy? The answer is -- theft.

Stealing energy from Jupiter

If you look closely at the mission trajectory, you'll see that when the spacecraft passes Jupiter, its direction changes:

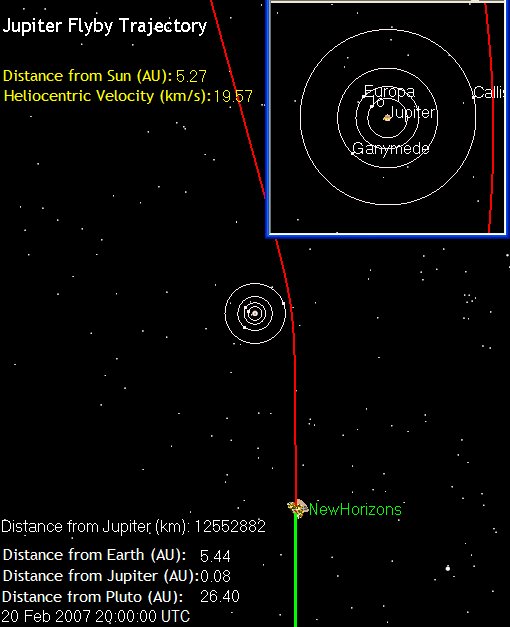
The gravitational forces between Jupiter and the spacecraft end up adding a new component to the spacecraft's velocity.

How does this work? Let's take a simpler collision as an example.

Joe stands by the side of the road and (very stupidly) tosses a tennis ball of mass m = 0.1 kg towards the road. As the ball hangs in mid-air, a giant truck of mass M = 10,000 kg smashes into it at speed V = 30 m/s.

After the collision, the ball flies forward at speed V₂ down the road, while the truck continues on its way with some (slightly smaller) speed V₁.

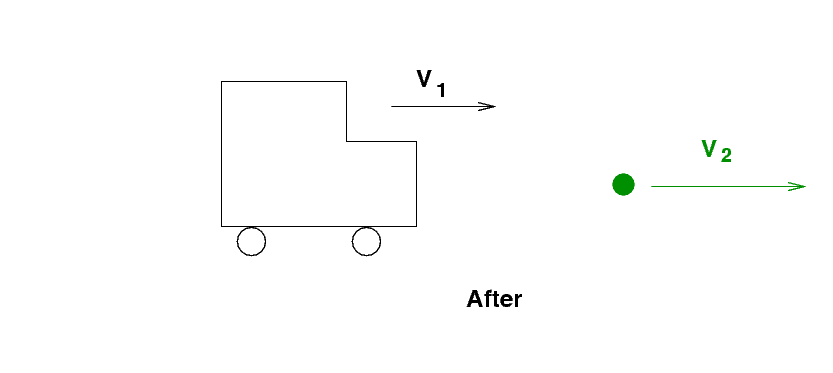
If this is an elastic collision, so that both momentum AND kinetic energy are conserved, can you figure out what the final speeds are?

The answer is that if a very massive object smashes into a low-mass object which is at rest, the very massive object slows down just a teeny-tiny bit, while the low-mass object zooms ahead at about twice the speed of the massive object. A very small amount of the original KE and momentum of the massive object is transferred to the low-mass object.

Something very similar is happening with the New Horizons spacecraft and Jupiter. Jupiter is majestically orbiting around the Sun at a speed of about 13,100 m/s. As the spacecraft slips behind Jupiter, the gravitational force of Jupiter pulls New Horizons forward. Because the spacecraft doesn't come _too_ close to the planet, only a portion of the maximum possible energy and momentum is transferred to the spacecraft: it picks up a transverse velocity of about 9700 m/s to go with its original radial velocity of about 19,600 m/s.

Why bother with this complicated manuever? The answer is that, using this orbital assist, New Horizons will reach Pluto more quickly.

Yes, the path is longer ...
the speed is much greater: about 21,900 m/s versus 19,600 m/s

The greater speed ends up cutting about 4 years from the total mission timeline; instead of reaching Pluto around 2019, New Horizons will reach it on July 14, 2015.

Going too fast?

So, when the spacecraft reaches Pluto, it will be moving at about 13,800 m/s. At its closest approach, the spacecraft will be only about 10,000 km from the planet's surface. Roughly how long will it take the spacecraft to zip past the planet?

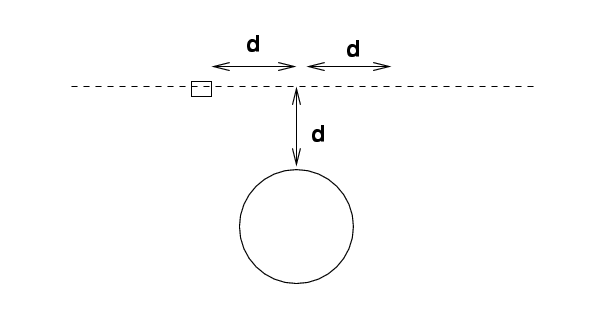
That's not very long -- it doesn't give the scientists much time to study the planet. Why doesn't the spacecraft use its rocket engines to slow down? It would be really nice to slow down enough to enter an orbit around Pluto -- that would require a final speed of about 800 m/s.



   Suppose exhaust speed is   u =  2,600 m/s 

   Mass of empty spacecraft   m =   480 kg

   Initial speed             vi = 13,800 m/s
 
   Final speed               vf =    800 m/s


   What would initial mass of the (spacecraft + fuel) have
   to be to yield this change in velocity?

The exhaust velocity I used above -- 2600 m/s -- is appropriate for a standard chemical mixture, such as that used in the big Saturn engines. Why didn't I choose numbers appropriate for an ion engine like the DS1? It would yield a much larger exhaust velocity, which would mean a much smaller amount of fuel needed. Why not use ion engines?

For more information

The official New Horizons web site
Animation showing the New Horizons trajectory
Celestia is a wonderful program for simulating a voyage through the solar system
- The Celestia home page is the place to download the program and documentation
- The add-on for the New Horizons mission
The NASA Gravity Assist Mechanical Simulator may help you to understand some of the manuevers of space missions.
New Horizons Mission Design (PDF) by Yanping Guo and Robert W. Farquhar, describes the factors that went into the choice of trajectory for the mission.