Benjamin Robins invents the ballistic pendulum

In the early 1700s, guns, cannons and all manner of artillery was used widely in warfare, but neither engineers nor scientists understood much of the physics of these weapons. For example, the speed of bullets or cannonballs was completely unknown.

Benjamin Robins (1707 - 1752), a British mathematician and military engineer, was the first to devise a practical method for measuring the velocities of projectiles. He described his work in New Principles of Gunnery, first published in 1742. At right is a picture of one of his inventions, the ballistic pendulum. Projectiles are fired horizontally so that they will strike the plate of wood GHIK, causing it to swing back in an arc around the pivot EF. As the plate swings, it pulls a ribbon W through a slot in the mounting; the length of ribbon is equal to the length of the arc through which the plate swings. Robins could use this arc length to compute the vertical distance through which the plate had moved, and so compute the change in its gravitational potential energy.

In one experiment, Robins tested a gun which fired a bullet with the following characteristics:

The bullet struck a plate of mass 56 pounds = 25 kg on a ballistic pendulum. Robins placed the pendulum at several distances from the muzzle of the weapon and made measurements which I have translated into metric equivalents. 



  Distance               25 ft           75 ft          125 ft
----------------------------------------------------------------
  vertical
  rise of plate         0.030 m         0.026 m         0.022 m

  
  speed (m/s) 


  KE (J)


----------------------------------------------------------------

Your job:

  1. compute the speed of the bullet at all 3 distances
  2. compute the kinetic energy of the bullet at all 3 distances
  3. compute the work done on the bullet by air resistance during the first interval (25-75 feet) and the second interval (75-125 feet)

Robins was able to use these measurements not only to determine the properties of various weapons, but also to determine the nature of the air resistance -- a very important job for the military!

The work done by air resistance on the bullet is complicated to compute properly. The problem is that the force depends on the speed of the bullet,

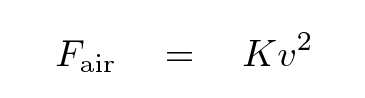
but that speed is constantly decreasing, so the force of air resistance is also constantly decreasing. That means that if we try to calculate the work done by air resistance as the bullet travels over some distance, we need to integrate a constantly changing force ...

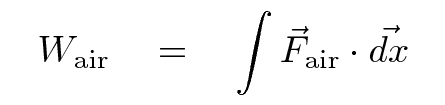
Ugh.

However, if we're willing to compromise and settle for results which are approximately correct, it's not so bad. Let's pretend that during one segment of its flight, the bullet has some average speed, and so some average force of air resistance. In that case, we can say

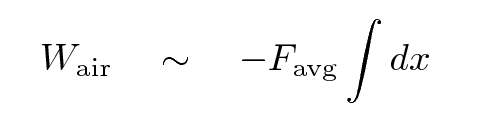
Let's use this approximation.

  1. what is the work done by wind resistance during the interval from 25-75 feet? from 75-125 feet?
  2. are these two amounts of work the same or different? Explain why
  3. compute the average force exerted by air resistance during each interval (and the second interval, if you have time)

Now, if we use the usual (simplified) formula for the force of air resistance,

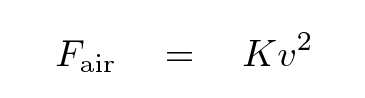
we can figure out the value of the coefficient K.

  1. what is the approximate value for the coefficient K?
  2. if this bullet was shot straight upwards, then fell back down towards the ground, what would its terminal velocity be?
  3. is that dangerous?

For more information