Blackbody Radiation and the Planck Function

A blackbody is an object which absorbs all the light which hits it: hence the name "blackbody". It also emits radiation, in a very particular manner.

Total energy emitted per second, at all wavelengths

The total amount of energy radiated per second by a perfect blackbody depends only on its temperature T and area A:

                                    4
     energy per second  =  sigma * T  * A

where

 
                                                          -8   Joules
      sigma  is the Stefan-Boltzmann constant =  5.67 x 10    --------- 
	                                                      s*m^2*K^4 

      T      is the temperature of the object, in Kelvin

      A      is the surface area of the object, in square meters

This relationship is called the Stefan-Boltzmann Law.

If we consider a patch of area exactly one square meter, then the energy radiated from it per second is

                                    4
     energy per second  =  sigma * T 
     per square meter

Energy emitted per second, as a function of wavelength

A blackbody doesn't emit equal amounts of radiation at all wavelengths; instead, most of the energy is radiated within a relatively narrow band of wavelengths. The location of that band varies with the body's temperature; for example,

           object                        T (Kelvin)      radiates mostly
 ------------------------------------------------------------------------
 very cold gas in insterstellar space        20             radio

 a live human being                         310             infrared

 the Sun                                  5,600             visible

 interior of nuclear explosion        3,000,000             X-rays

The exact amount of energy emitted at a particular wavelength lambda is given by the Planck function:


                        (2*h*c^2) / lambda^5
       B    (T)   =    ----------------------
	lambda             h*c/lambda*k*T
		          e               -  1

Or, in beautiful typeset format,

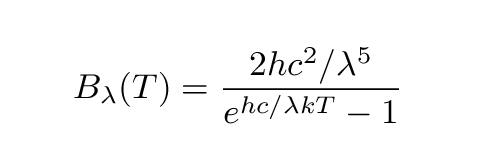
In this equation,

           B     (T)        is the energy (Joules) emitted per second per unit
            lambda                 wavelength per steradian from one square meter
                                   of a perfect blackbody at temperature T

           T                is the temperature of the blackbody

	   h                is Planck's constant      =  6.63 x 10^(-34) J*s

	   c                is the speed of light     =  3.00 x 10^(8)   m/s
 
	   lambda           is the wavelength 

	   k                is Boltzmann's constant   =  1.38 x 10^(-23) J/K

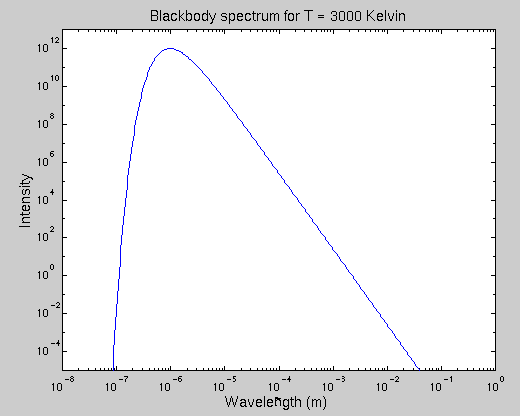
The Planck function has a distinctive shape: it rises very sharply at short wavelengths (due to the exponential), reaches a peak at some wavelength, then falls gradually at longer wavelengths.

Integrating the Planck Function

In order to find the total energy emitted per second in some wavelength range

              lambda 1  < lambda  < lambda 2

from one square meter of a perfect blackbody, one can integrate the Planck function

                       lambda 1
                          /          (2*h*c^2) / lambda^5
   energy emitted  =      |         ----------------------   d(lambda)
     per second           /             h*c/lambda*k*T
  per square meter     lambda 2        e               -  1
    per steradian

and then multiply by (pi) steradians (we are interested in the energy emitted at all angles from one face of a flat plate, so we integrate over solid angle to cover half the sky; that ends up being the same as multiplying by a factor of (pi) = 6.28...)

Or, in nicely typeset form,

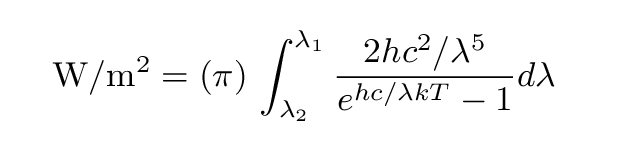
Obviously, if one integrates from the shortest possible wavelength (lambda = 0) to the longest possible wavelength (lambda = infinity), and multiplies by (pi), one ought to end up with the same total energy emitted per second as given by the Stefan-Boltzmann Law,

                                    4
     energy per second  =  sigma * T 
     per square meter

Last modified 4/06/2007 by MWR.