Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
See Chapter 6 of your textbook for more information on these methods.
The differences between "open" and "closed" methods
The differences between "open" and "closed" methods are
closed open
----------------- ---------------------
uses a bounded interval not restricted to interval
(usually) converges slowly (usually) converges quickly
always finds a root may not find a root
(if it exists) (if it exists)
This method uses not only values of a function f(x), but also values of its derivative f'(x). If you don't know the derivative, you can't use it.
The graphical approach to the method may be described as "follow the slope down to zero"; see your textbook for an illustration.
One can also use the Taylor series to derive Newton's method. The problem is: given
Suppose we expand the function around the starting point, using the Taylor series:
f(x) = f(x1) + f'(x1) * (x - x1)
Now, we want to find the spot where f(x) = 0, so
let's plug that into the equation and solve for x.
0 = f(x1) + f'(x1) * (x - x1)
-f(x1) = f'(x1) * (x - x1)
-f(x1)
------- = x - x1
f(x1)
f(x1)
x = x1 - ------
f'(x1)
So, given a first point x1, one can calculate a new guess x2 which -- we hope -- is closer to the root. Iterating a number of times might move us very close to the root.
But there is no guarantee that this method will find the root. The method often does, but it can fail, or take a very large number of iterations, if the function in question has a slope which is zero, or close to zero, near the location of the root. It can also fail if the second derivative of the function is zero near the root.
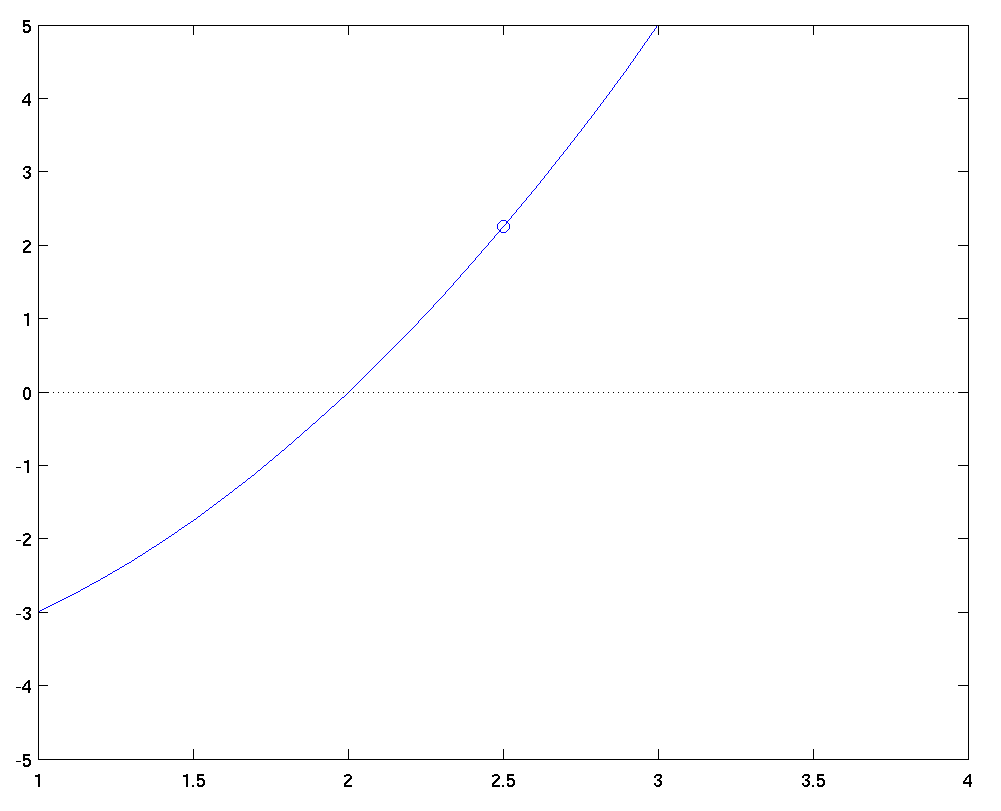
Let's look at a specific example of Newton's method:
find a root of the equation y = x^2 - 4 on interval [0, 5]
stop when relative fractional change is 1e-5
The exact root is 2, of course.
How quickly can we find it, to within the given termination criterion?
The first step is to pick a starting point -- why not try halfway between the endpoints, at x1 = 2.5? The function has a value of f(x1) = 2.25 there ...
Now, we calculate the derivative of the function at x1 = 2.5, which is f'(x1) = 5.0. So, we draw a line with slope 5 downwards from our current point, and follow it to the x-axis.
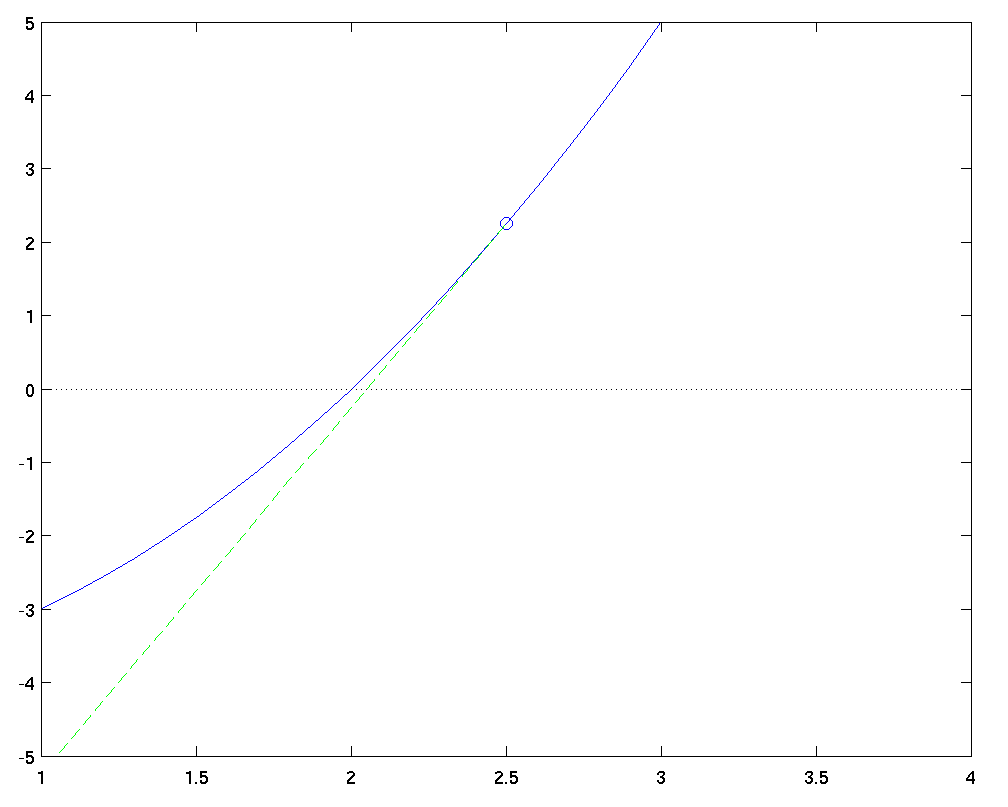
Where does this line intercept the x-axis? At the point given by
f(x1)
x2 = x1 - ------
f'(x1)
which turns out to be our next guess at the root:
x2 = 2.05
We are now much closer to the root than we were at the start -- hooray! Newton's method sure is fast, when it works. Let's zoom in and repeat the process. We evaluate our function at the new position, finding f(x2) = 0.2025.
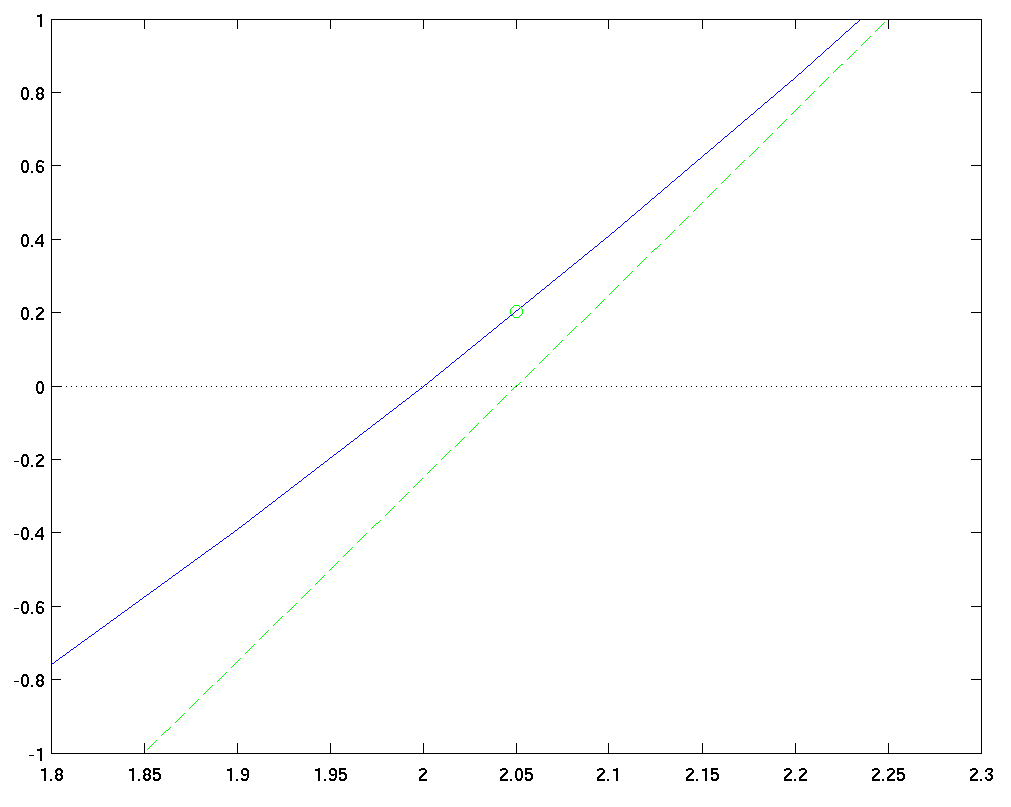
We also evalulate the derivative of the function at this point, which yields a new slope: f'(x2) = 4.1. Following this new slope down to the x-axis, we see that it intersects at
f(x2)
x3 = x2 - ------
f'(x2)
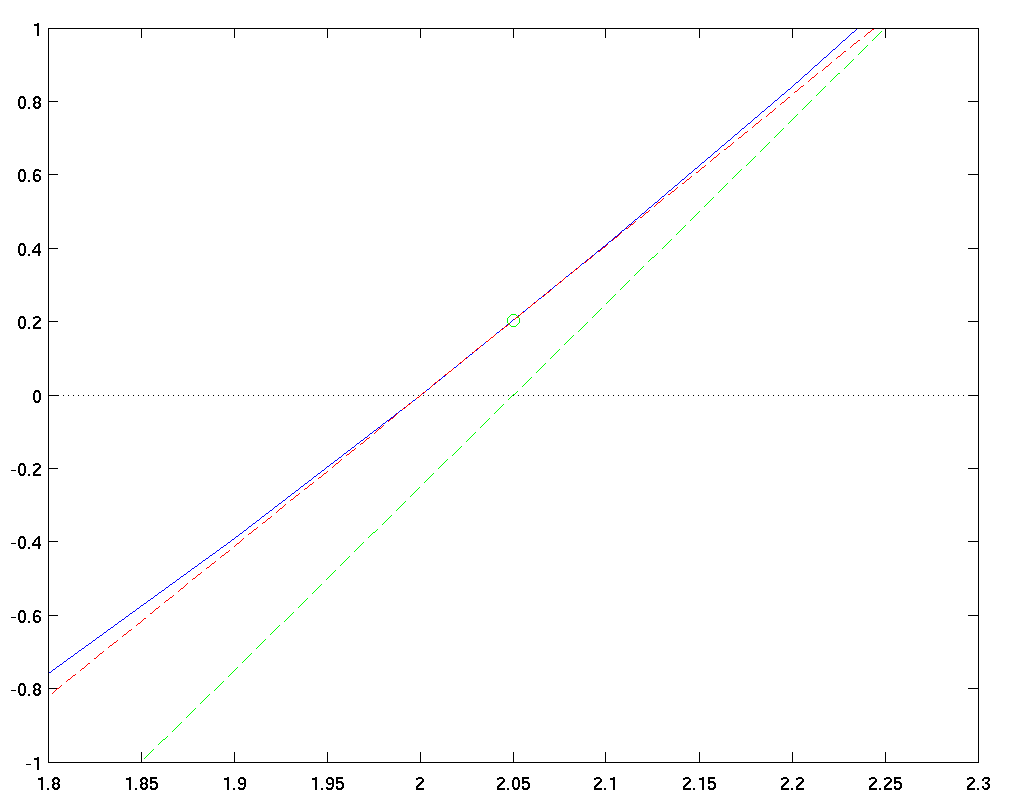
Wow. This third estimate of the root, x3 = 2.00061, is really, really close to the actual root (which is 2, of course). In just two steps, Newton's method has done very well.
You can watch the progress of Newton's method in these movies:
Here's a table showing the method in action:
current value at value of deriv fractional
iter guess current guess at current guess change
-------------------------------------------------------------------
0 2.500000e+00 2.2500e+00 5.0000e+00 2.1951e-01
1 2.050000e+00 2.0250e-01 4.1000e+00 2.4688e-02
2 2.000610e+00 2.4394e-03 4.0012e+00 3.0483e-04
3 2.000000e+00 3.7169e-07 4.0000e+00 4.6461e-08
The result is 2.00000000000000, which is indistinguishable from the true root of 2.
In order to use Newton's method, we need to be able to calculate the derivative of a function at some point: f'(x1). Sometimes you don't know the derivative; what can you do then?
What you can do is estimate the derivative by looking at the change in the function near x1: pick some other point x2 close to x1, and estimate the derivative as
f(x1) - f(x2)
derivative at x1 is approx D = -------------
x1 - x2
With that approximation in hand, you can then apply the same method to guess the point at which the function equals zero.
f(x1)
x_new = x1 - ------
D
After finding x_new, one can replace
x1 = x_new
x2 = x1
and make another iteration, and so forth.
The secant method therefore avoids the need for the first derivative, but it does require the user to pick a "nearby" point in order to estimate the slope numerically. Picking a "nearby" point which is too far, or too near, the first one, can lead to trouble. The secant method, just like Newton's method, is vulnerable to slopes which are very close to zero: they can cause the program to extrapolate far from the true root.
Last modified 3/25/2003 by MWR.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.