Numerical Integration: Intermediate

• Rectangle method
• Trapezoid method
• Simpson's 1/3 method
• Tradeoffs between the methods

The Rectangle Method

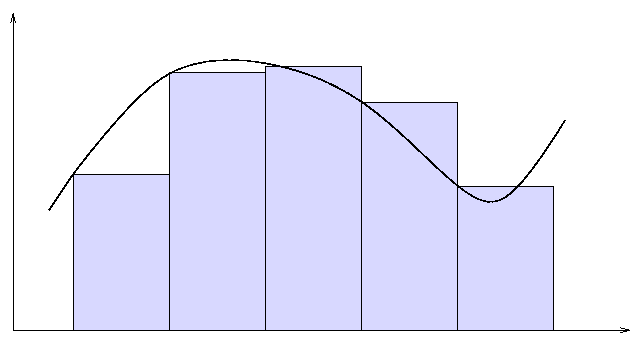
You have already used the very simple rectangle method to integrate a function. It assumes that the function has a constant value within each little interval.

• break the interval into a number of pieces of equal width
• evaluate the function at x, the start of each piece
• calculate the area of a rectangle for each piece

    area =  height * width  =  f(x) * width
  

• add up the areas of all the rectangles

A picture of the rectangle method looks something like this:

The Trapezoid Method

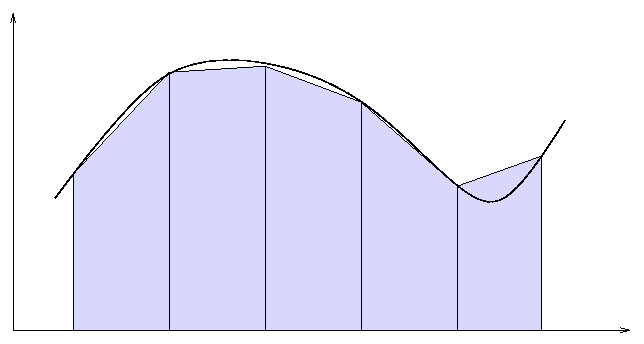
The trapezoid method uses information from both the start and the end of each little piece to make a better estimate of the area under the curve. It assumes that the function may change linearly within each piece.

• break the interval into a number of pieces of equal width
• evaluate the function at x1, the start of each piece
• evaluate the function at x2, the end of each piece
• calculate the area of a box with a linearly sloping top for each piece

                                        1
    area =  (avg. height) * width  =    - [f(x1) + f(x2)] * width
                                        2
  

• add up the areas of all the boxes

A picture of the trapezoid method looks something like this:

Simpson's 1/3 Method

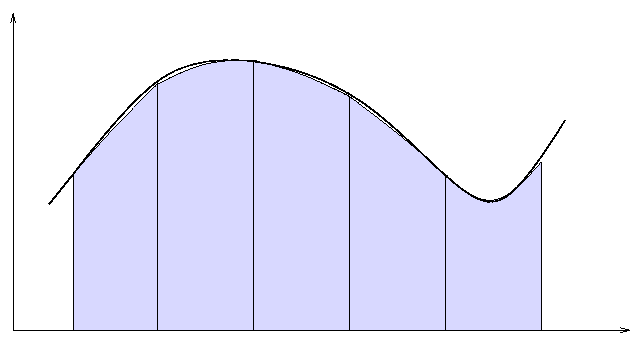
The idea behind Simpson's 1/3 Method is to evaluate the function at three points within each little interval, and then to calculate the area underneath a parabola fitted to those three points.

• break the interval into a number of pieces of equal width
• evaluate the function at x1, the start of each piece
• evaluate the function at xm, the middle of each piece
• evaluate the function at x2, the end of each piece
• calculate the area of a box with a parabolic top for each piece

                                           1
    area =  (Simpson's height) * width  =  - [ f(x1) + 4f(xm) + f(x2) ] * width
                                           6
  

• add up the areas of all the boxes

A picture of Simpson's method looks something like this:

Tradeoffs between the methods

Which method is best? Well, it depends on your criteria. There are several ways to rank them.

1. Easiest to remember: The rectangle method

2. Easiest to write correctly: The rectangle method, again

3. Number of function evaluations: The rectangle method evalulates the function once for each little interval, whereas the trapezoid method evaluates it twice, and Simpson's method three times. If the function is a long, complicated one, the extra evaluations might take too much time.

4. Accuracy: For a fixed number of intervals, Simpson's method is almost always the best.

5. Scaling: All methods improve as one increases the number of little intervals, but Simpson's method improves much more quickly than the others.

Because computers today are so fast, the good old rectangle method isn't as bad a choice as you might think. In order to reach some desired accuracy, one may (often) just crank up the number of intervals do a ridiculous value, without having to wait for the answer. But if your first attempts via the rectangle method do indicate that it's not going to work in some particular situation, I recommend jumping to Simpson's method.

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.