Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
See Sections 25.2 of your textbook for more information on these methods.
Recall that Euler's method provides a simple means for calculating new values of some physical quantities, based upon their current values. In the case of a man falling through the air (without air resistance), the variables are:
t = current time
i
t = next time
i+1
v = current velocity
i
v = velocity at next time
i+1
a = current acceleration
i
Euler's method provides this blueprint for calculating the future values, based on the current ones:
v = v + a * (t - t )
i+1 i i i+1 i
y = y + v * (t - t )
i+1 i i i+1 i
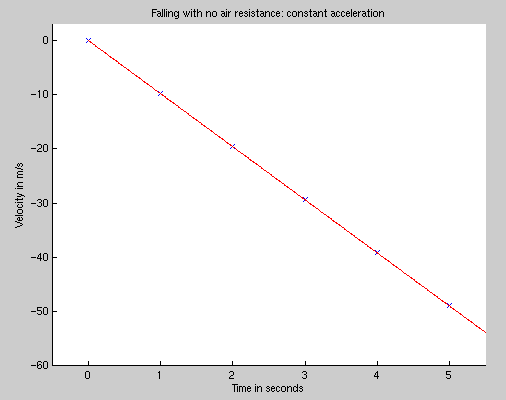
Which produces the following values of velocity versus time, near the start of the fall (blue crosses are results of Euler's method, red line is actual, exact solution):
So, Euler's method uses the current values of acceleration and velocity, and assumes that those quantities don't change over the coming timestep. In this case -- no air resistance -- it works well. And it should, because the change in velocity really is a constant in each timestep: the velocity changes by exactly -9.8 meters per second each second.
In real life, velocity might not change in such a simple fashion. In that case, is there any way to improve the estimate? Sure! If we know that the acceleration and velocity are probably going to change -- why not try to take that into account?
It will help a bit in describing how to improve the estimates of acceleration and velocity if I add a little complication to the system. Let's now allow include air resistance in the problem. The force of air resistance depends on the cross-section area of the jumper, the air density, and some other stuff, and it also depends on the velocity with which he falls. Let's describe it as
2
force of air resistance = K * v
where K is some constant the depends upon the density
of air, cross-section area, etc.
This means that the net force on the jumper is
2
F(net) = -mg + Kv
and his acceleration is therefore
dv F(net) K 2
-- = a = ------ = -g + --- v
dt m m
Now, the velocity doesn't change by a constant amount each second; its change depends in part upon the value of velocity, squared. This is a differential equation, which is not so easy to solve analytically.
Okay, let's write down Euler's method, applied to this problem:
v = v + a * (timestep)
i+1 i i
K 2
= v + [ -g + --- v ] * (timestep)
i m i
If we use use Euler's method for this problem, we find that it doesn't work quite so well; again, in the plot below, blue crosses represent values derived by Euler's method, and the red line represents the exact solution:
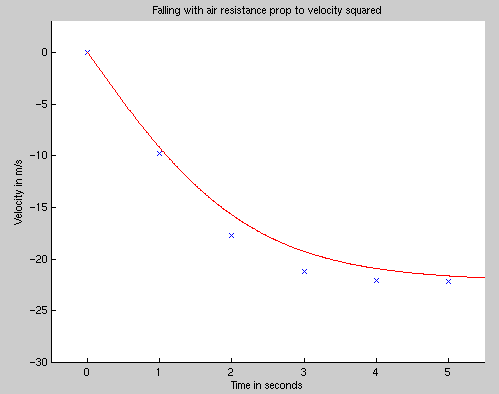
In this case, Euler's method overshoots the true solution. At the start of the jump, the force of air resistance rises during the course of each second, as the jumper falls more and more rapidly. That means that the acceleration calculated with the current velocity will overestimate the actual acceleration during that next timestep.
So, the physical quantities (velocity and position) are changing during each timestep. One way to improve our calculation is to predict how much they are going to change, and then use that information to correct our naive extrapolation of the current conditions. This idea forms the basis for predictor-corrector methods of integration.
There are many ways to estimate changes during the next timestep. The simplest is called Heun's method.
The basic idea is that, if we knew (for example)
and
Let v = current velocity
i
a = acceleration based on current velocity
i
v = (poorly predicted) future velocity
i+1
a = (poorly predicted) acceleration based on future velocity
i+1
Then a better guess at his acceleration over the next timestep is
1
a = --- (a + a )
avg 2 i i+1
And then we can use this average acceleration to make an
improved calculation of his motion.
Written as an algorithm, Heun's method looks like this:
LOOP:
% first, we calculate the current acceleration
current_acceleration = function(current_velocity, etc.)
% we use this to do a poor job of estimating future velocity
future_velocity = current_velocity + new_acceleration * timestep;
% use (poorly predicted) future velocity to calc future acceleration
future_acceleration = function(future_velocity, etc.)
% find the average acceleration
acceleration = 0.5 * (current_acceleration + future_acceleration)
% use the average acceleration
new_velocity = current_velocity + acceleration * timestep;
(go back to top of loop)
Does Heun's method do better? Yes, in two ways!
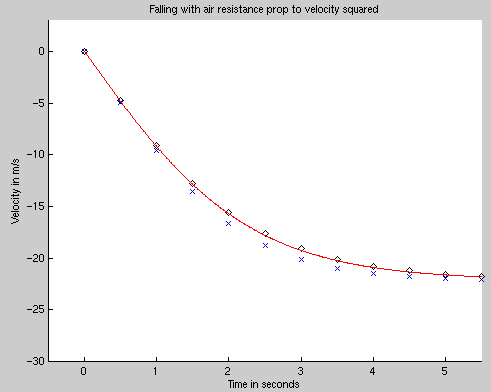
Let's see this in action. Here's a comparison of the velocities calculated via Euler's method (blue crosses) and Heun's method (black diamonds), using a timestep of 0.5 seconds.
Here's a closeup near t = 2 seconds .
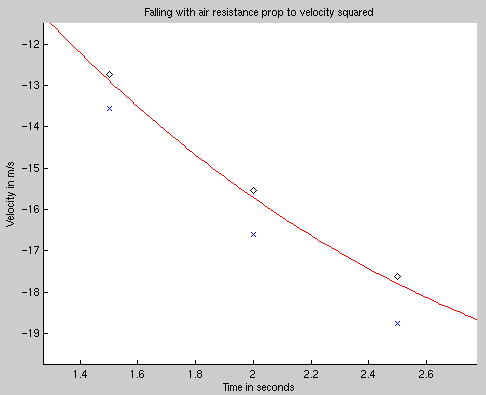
Now, if we decrease the timestep size from 0.5 to 0.2 seconds, both methods improve -- but by different amounts. Here's another closeup of the region around t = 2 seconds; note how much closer Heun's method is to the actual velocity now.
The difference between Heun's method and Euler's method is analogous to the difference between the Trapezoid and Rectangle methods you used earlier.
Rectangle method assumes constant value Euler's method assumes constant
for function within each interval value for derivative within
each interval
Trapezoid method assumes linear change Heun's method assumes linear
in function within each interval change for derivative within
each interval
Another way to say this is to characterize the Rectangle and Euler methods as zero-th order, but the Trapezoid and Heun methods as first order. There are higher-order methods, of course: Simpson's method is second-order, and there are analogous second-order methods in the derivative domain (see Section 25.3 for an example of a second-order Runge-Kutta algorithm).
In general, higher-order methods require
Additional sources of information on integration schemes are
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.