And now, for your amusement and stimulation,

Vampire Population Ecology

 

Introduction

~or~

A Little Math Never Hurt Anyone

We are gathered here today to ponder the ways in which the humans and vampires of Sunnydale interact.  Specifically, Betsy asked:

 

Ooh, Brian, can you help us work out the vampire carrying capacity of a typical

population? I'm assuming a typical vampire accounts for, say, 150-200 humans a

year. So how big does a town have to be to support Sunnydale's apparently

limitless supply of vampires?  Are there human warrens in the catacombs

somewhere, used only for feeding purposes?  

 

The term “carrying capacity” isn’t often applied to predator population dynamics.  Instead, ecologists generally estimate stable predator populations by first coming to grips with the prey’s population dynamics, including its carrying capacity.  Actually, in a lot of different cases, the prey’s carrying capacity ultimately determines how well the predator does. 

 

In principle, ecologists might employ two basic strategies to get at a problem like this.  The empiricists would go out and find a field site where they could actually observe predators and their prey, and just tally the results over time.  The theoreticians would chuckle at the empiricists, and construct mathematical models that probably approximate the behavior of populations in the field, keeping their hands more or less clean in the process. 

 

In real life, most ecologists use both strategies off and on.  Unfortunately, I don’t know of any real life vampire populations in the field, so we’re going to have to pretend that we are strict theoreticians.  That means that we’ll be using math: some algebra, some calculus, and some matrix theory.  This is O.K.!  It hurts a lot less than, say, getting bitten by a vampire as you’re trying to fit the bugger with a radio collar. 

 

A Model

What follows is based on some of the simpler theoretical understandings of predator-prey population dynamics.  I’m assuming that human populations are not controlled solely by vampire predation (i.e.- in the absence of vampires, the human population would still eventually be limited by some other factor, like food supply, disease, or access to a well-written weekly news magazine.  I like The Economist myself, but that’s clearly a digression). 

 

If we let H stand for the size of the human population and V stand for the size of the vampire population, then we can represent the changes in each population over time with a pair of differential equations:

 

                                   

 

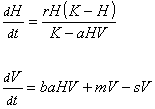
            where   r           is the intrinsic growth rate of the human population, incorporating

                                                natural rates of both birth and death as well as immigration

                        K         is the human carrying capacity of the habitat in question

                        a          is a coefficient that relates the number of human-vampire

                                                encounters to the number of actual feedings

                        b          is the proportion of feedings in which the vampire sires the victim

                                                            (i.e.- this is the vampire birth rate)

                        m         is the net rate of vampire migration into Sunnydale

                        s           is the rate at which the Scoobies stake vampires (assumed to be the

                                                only important source of vampire deaths). 

 

 

What we need to do, simply put, is find the equilibria that exist between these two equations.  In other words, we need to find the combination(s) of human and vampire populations sizes that satisfy both equations at the same time.  As it turns out, there are three such equilibria.  Without showing you the really ugly math (after all, this is a family forum), I’ll just say that two of the equilibria are not very interesting.  They are 1) when both the humans and the vampires are completely extinct, and 2) when the vampires are extinct but the human population hovers at or near its carrying capacity.  The third equilibrium is the one we care about, wherein humans and vampires coexist.  At that point, the solutions are:

 

                                   

 

Notice that the actual human population doesn’t depend on carrying capacity at all, and that the vampire population does!  yes, only an ecologist could put an exclamation point after a statement like that…  We know from the existence of our other equilibria that the human population is not necessarily big enough to support a vampire population.  What we need to know is whether or not the human carrying capacity is large enough.  Specifically, if K is too small, then

                                      

 

and the equilibrium vampire population size will be negative.  Basically, the human population’s carrying capacity must be higher than its equilibrium abundance:  

 

                                   

 

If this isn’t the case, then the even largest possible human population isn’t large enough, and vampires have no hope in this particular region. 

 

A Trial

Now that we have a model, we can start trying out some assumptions (or, if we’re lucky, actual measurements) for the various parameters.  To start with, we know from the sign in “Lover's Walk” that the human population of Sunnydale is 38,500.  We also know that the town of Berkeley, CA has a population of about 100,000.  Since Berkeley is also a town with a UC campus, and is furthermore a town that has been more or less completely urbanized (the population has been stable or dropping slightly for about 25 years), we will take 100,000 as the carrying capacity for a California university town. 

 

Let’s assume the following:

            Sunnydale’s human population growth rate is 10% annually, which is at the high

                        end for a budding California community.

 

            A vampire feeds every three days, and encounters about one hundred potential

                        victims in the course of a day, meaning that 1 out of every 300 encounters

                        involves a little refreshment.

 

            An individual vampire sires a victim every other year, or once per 240 feedings.

 

            Buffy and her Slayerettes, busy little beavers that they are,  annually stake about

                        1/3 of the vampires plaguing Sunnydale.

 

            Vampires are flocking to Sunnydale, since the Hellmouth is the underwordly

                        equivalent of Silicon Valley, and the demon labor market is just too good

                        to be true.  Thus, we’ll assume a yearly migration rate of about 10%, or

                        the same as for the humans.

 

In terms of our model, we have:

            r = 0.0953

            a = 0.00333

            b = 0.00417

            s = 0.600

            K = 100000

            m = 0.0953

 

            note that for r, s, and m I’ve pulled a little switcheroo.  In our assumptions, we

            speculated as to the yearly rates of growth or migration or what-have-you.  But

            our model is based on a set of continuous, exponential functions, rather than

            discrete time step geometric functions.  For our assumptions to make sense in the

            context of our model, I’ve had to perform a natural log transformation of the

            yearly rates.  For example,

 

                         

 

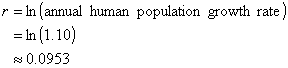
So now we can plug these numbers into our system of equations, and solve for the equilibrium populations of humans and vampires (, respectively).  What we get is an equilibrium human population of  36,346, and an equilibrium vampire population of around 18.  Holy cow!  We just about nailed the human population, and the number of vampires certainly fits with the number you might expect, assuming that at any given time there is a lair or two that Buffy doesn’t know about yet. 

 

But Can It Last?

Now, the number of vampires clearly fluctuates over time.  What we don’t know yet is whether or not these fluctuations are sufficient to prevent the equilibrium state from ever existing.  In other words, is this equilibrium we’ve discovered stable?  Imagine, if you will, a house of cards.  Under the right circumstances, you can achieve an equilibrium structure.  If I’m not the one who built the house of cards, this equilibrium structure may even be sophisticated and graceful.  But if a breeze comes through the window at the wrong time, the equilibrium structure crashes in very short order.  What about our system of human and vampire populations? 

 

Mathematically, we need a little bit of matrix algebra.  We start by constructing a Jacobian matrix, which is an array of the derivatives of each differential equation with respect to our two population sizes.  The eigenvalues of the Jacobian matrix will indicate whether the equilibrium is stable (by whether or not both eigenvalues are negative) and whether the system will exhibit ocillation (by whether or not the eigenvalues contain imaginary numerical components). 

 

We could do all of that right here, but frankly I don’t enjoy it.  Besides which, I can just about guarantee that you are more interested in the ecology of vampire populations than in their theoretical mathematical peculiarities.  So instead, we can just plot the results of our model using actual numbers: we’ll start with arbitrary “initial population sizes”, and let the model run through time. 

 

The following graph shows human population sizes on the horizontal axis and vampire population sizes on the vertical axis.  Each line represents a trajectory through time, and any point on a line represents a combination of human and vampire population sizes – a step, if you will, in that beautiful dance between Buffy and the Minions of Evil.  Notice that wherever we “start” the trajectories, they all spiral in towards our equilibrium state, indicated in the center by an asterisk. 

 

 

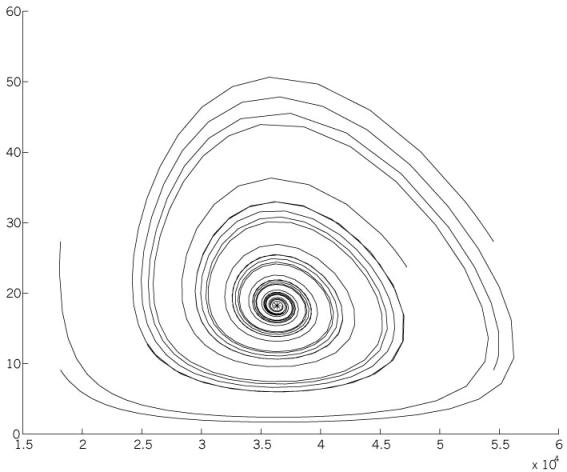
The spiral pattern is referred to as a “stable focus”, and it indicates that the ecological system in Sunnyvale is probably fairly tolerant of the ebbs and flows of vampire activity.  Of course, there is always a possibility that some combination of events (such as, by way of illustration, the Apocalypse) that would bump this system out of its comfy little trough, and then all bets are off. 

 

Wrapping Up

Obviously, this is a very simplified model, and it is very vulnerable to flawed assumptions.  For example, our guesses as to how often vampires feed and sire could be well off the mark.  And to be fair, I’ll tell you that my first order guesses, while probably not too far off, were chosen at least partly to obtain a reasonable result on our first try.  In addition to our parameter assumptions being vulnerable, we may have made mistakes in the overall structure of the model.  For example, we know that vampires can live (albeit miserably) on non-human prey.  We’ve also heard from Spike that while vampires can starve, they don’t actually starve to death.  Incorporating these facts into the model might give some very different results. 

 

At any rate, we can give the following synopsis:  “About time!”, you mutter, shaking your head…

Although the creators and writers of “Buffy the Vampire Slayer” are probably not theoretical ecologists, and although we are consistently amazed by the depth and sophistication of their fabricated milieu’s continuity, it is downright nifty that the show appears to make ecological sense. 

 

Brian Thomas is a PhD candidate in ecology at Stanford University in California.  He used MATLAB (running on a Sun Solaris 2.7 workstation and commanded remotely through Telnet) to manipulate equations and run the model.  He’d like to thank Dr. Joan Roughgarden for teaching him the vast majority of what he knows about population dynamics, and he would be very interested in hearing your thoughts on this little treatise, because he is keen on spending a goodly portion of his career communicating science to intelligent but non-technical audiences (like you!).