Examples of the Uncertainty Principle in action

Let's make a very, very simple model of a hydrogen atom. We know that atoms are about 0.1 nm, or about 1 Angstrom, in size. So our model will be an electron flying inside a box of length L = 0.1 nm

What is the average position of the electron relative to the center of the box?
What is the average momentum of the electron relative to the center of the box?
What is the typical uncertainty in the position of the electron?
What is the corresponding uncertainty in the momentum of the electron?

Now, suppose once again that for rough purposes, the typical magnitude of an electron's momentum is of order its uncertainty.

What is the typical speed of an electron?
Is this relativistic?
What is the typical KE of an electron? Express your answer in both Joules and eV.

How does this compare to the ground state energy of a real hydrogen atom?

As we shall see next week, a somewhat more sophisticated model of the hydrogen atom postulates that the electron orbits the nucleus, but that it may do so only in discrete orbits.

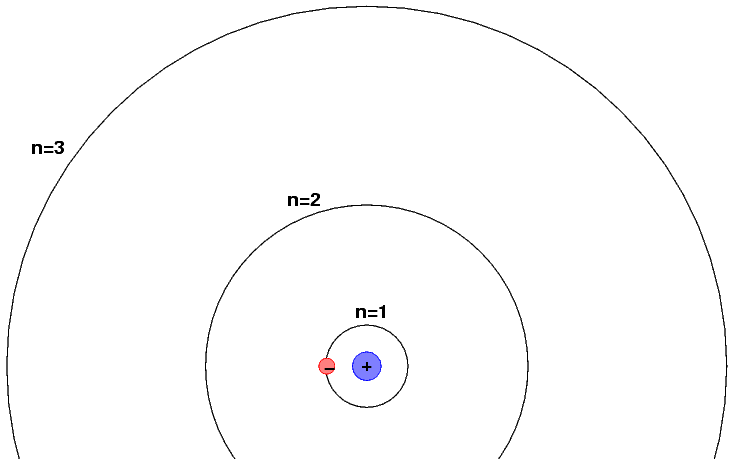
When an atom jumps from one orbit -- say, n=3 -- to a lower orbit -- say, n=2, -- it emits a photon. The energy of the photon must be equal to the difference in energy between the upper and lower orbit. For today's purposes, we can label the energy in each state as



       E (n=3)   =   1.89 eV

       E (n=2)   =   0    eV

What is the difference in energy between these two levels?
What is the wavelength of light which is emitted if a hydrogen atom decays from the n=3 to the n=2 state?

It turns out that this decay (and most others for hydrogen) occurs very, very quickly. The lifetime in the upper state is only about 10^-8 seconds. That means that if one tries to determine the energy of an atom while it is in this upper state, one is limited to a measurement lasting about

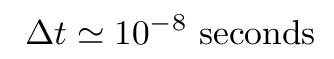
What is the uncertainty in the energy of the upper level?
What is the FRACTIONAL uncertainty in the energy of the upper level?

If we have a whole bunch of hydrogen atoms in the excited state, then some will have exactly the expected energy in the excited state, but others will have slightly more, and others slightly less. That means that if we watch as this gas emits (or absorbs) photons, they will have a small range of energies centered on 1.89 eV; and, therefore, a small range of wavelengths centered on 656.3 nm.

Consider an atom which has a little extra energy in the upper state, E + &Delta E, and then decays to the lower state. It will emit a photon with a little more energy than usual.

What is the energy of this photon?
What is the wavelength of this photon?
How large a spread in wavelength should we see if look at light emitted by a large sample of photons?

If we look at the spectrum of light from the Sun, we can zoom in on the region around this wavelength. It is (as you will learn next week) sometimes called the "Balmer-alpha" or "hydrogen-alpha" transition. Here's a small section of the spectrum. We are seeing an absorption line, not an emission line, but the principle is the same. The smaller dips are much weaker absorption lines due to other elements and ions.

What is the actual width of the H-alpha line in the Sun?
How does it compare to the width you calculated based on the uncertainty principle?

It turns out that the natural broadening of this line caused by the uncertainty principle is overwhelmed by broadening caused by other physical processes. See homework problem number 8 on assignment 5 for a similar situation.