An example of using the Uncertainty Principle

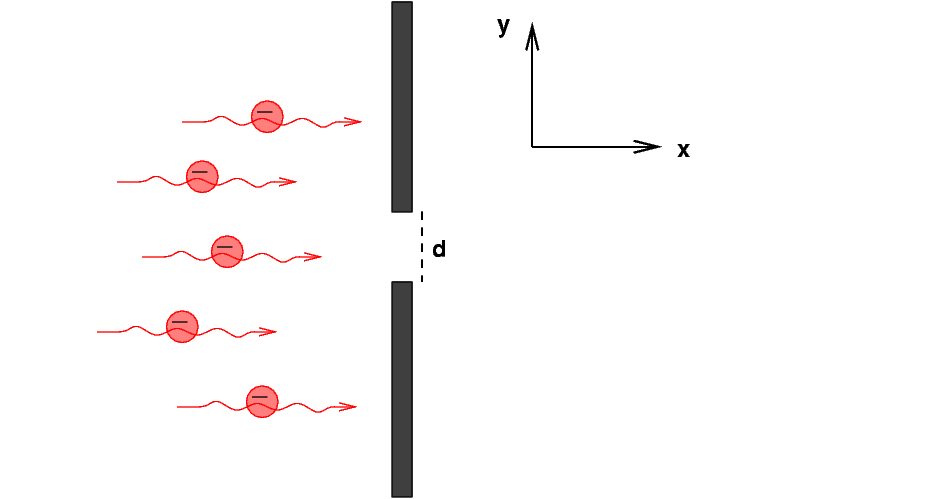
Suppose that we create a beam of electrons, all flying in the x-direction with some speed v_x; let's make this speed small compared to the speed of light, so that we can ignore relativistic effects. That will simplify the math a bit.

We shine this beam of electrons at a wall which has a slit of width d in it.

What happens when the electrons pass through the slit? There are two ways we can approach this problem:

use deBroglie's hypothesis to treat the electrons as waves, and then apply the classical diffraction formula
use Heisenberg's ideas about uncertainties

Let's try the uncertainty method first. Before the electrons reach the wall, they are moving purely in the x-direction. That means that their velocity in the y-direction must be zero; and, if their motion is truly in the x-direction alone, the uncertainty in their velocity in the y-direction must also be zero. Thus, the uncertainty in their y-momentum must also be zero.



  Q:  If the uncertainty in y-momentum is zero,
      what do we know about the y-position
      of each electron before it strikes the wall?

The answer

The electrons reach the wall. Most hit the wall and are absorbed or reflected, but some pass through the slit and continue to the right.



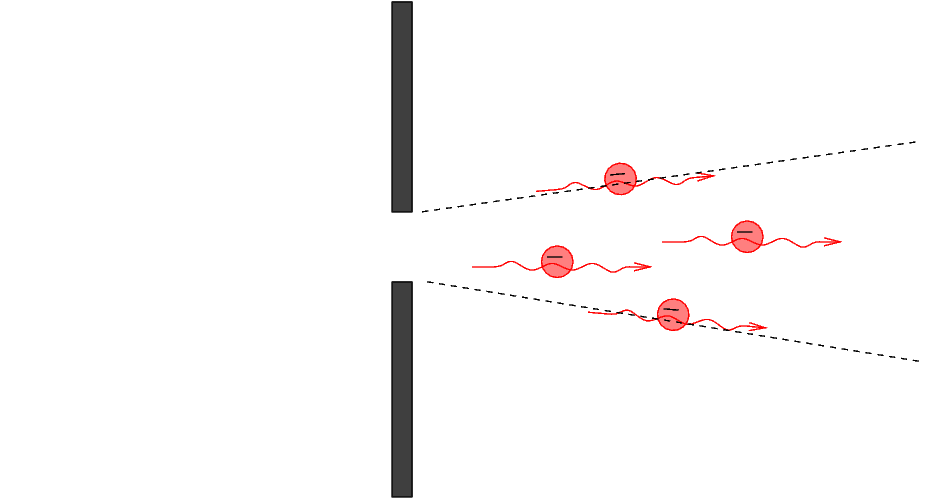
  Q:  What do we know about the y-position of
      any electron which passed through the slit?

  
      What constraints does this place on the
      y-momentum of the electrons which pass through
      the slit?

The answer

Looking at the electrons which passed through the slit, we see that although the average y-momentum is zero, there is now a small range of values around zero.

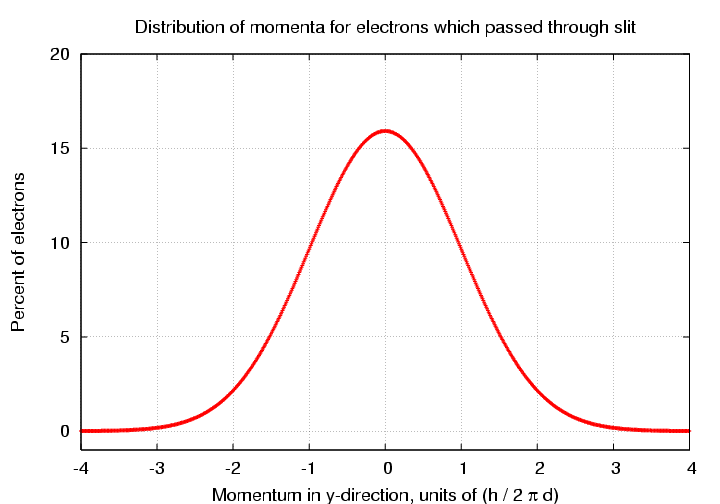
There are several different ways one can describe the width of this distribution. Let's pick a simple one: the typical magnitude of the momentum in the y-direction is just

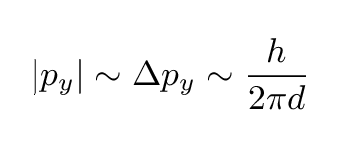
That means we can now draw the direction of an electron which is at a typical angle from the center:



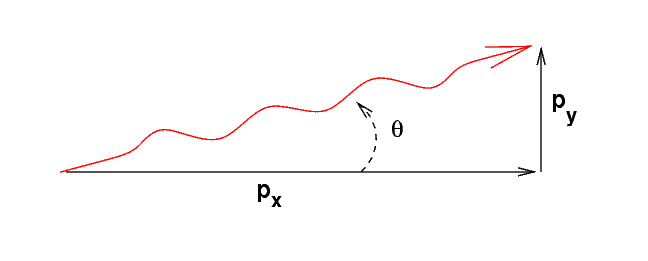
  Q:  What is the momentum in the x-direction for these
      electrons?


  Q:  Assume that the angle theta is small, so that
      the y-momentum is much smaller than the x-momentum.
      Using deBroglie's formula, express the electron's
      momentum in terms of its wavelength.


  Q:  Derive an expression for the typical angle, theta,
      by which the beam of electrons will spread.

The answers

Okay, that's one way to look at it. Suppose that we instead look at this experiment using deBroglie's formula to turn the electrons into waves, and then apply classical diffraction theory.



  Q:  What is the wavelength of the electrons 
      before they strike the wall?


  Q:  At what angle theta will the first dark
      spot appear in a classical diffraction pattern?

The answers

Aha! The answer is basically the same, whether we approach the problem using uncertainty, or using diffraction theory. That's a good sign that the uncertainty principle is correct.