Uncertainty, in waves and matter

You've probably heard of the famous Uncertainty Principle of Heisenberg, which says something like

You can measure the position of an electron, or the velocity of an electron, but you can't measure both at once.

But what is the source of this principle? Is it something that just came to Heisenberg out of the blue? Is it completely unconnected to the rest of physics?

No and no.

There is a reasonably straightforward way to see that there must be some relationship between position and velocity; just start with waves.

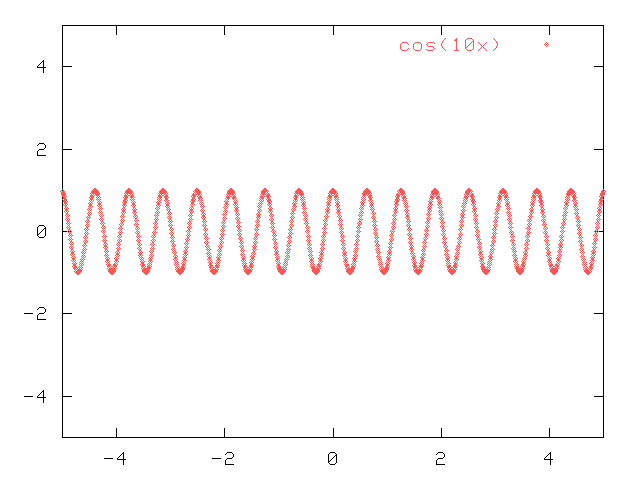
Uncertainty relationships for waves

Consider a simple cosine wave, such as

        y(x)  =  cos(10*x)

If we plot this wave as a function of x, we see a graph like this:


  Q:  What are the units of x in this graph?

Suppose we have a source of waves -- say, an earthquake. If we set up a string of seismic sensors along a highway, we can measure the height of the ground as the earthquake's waves move through the ground. We put sensors every few centimeters along a road. During the earthquake, at one particular instant, a plot of height versus position might look like this:

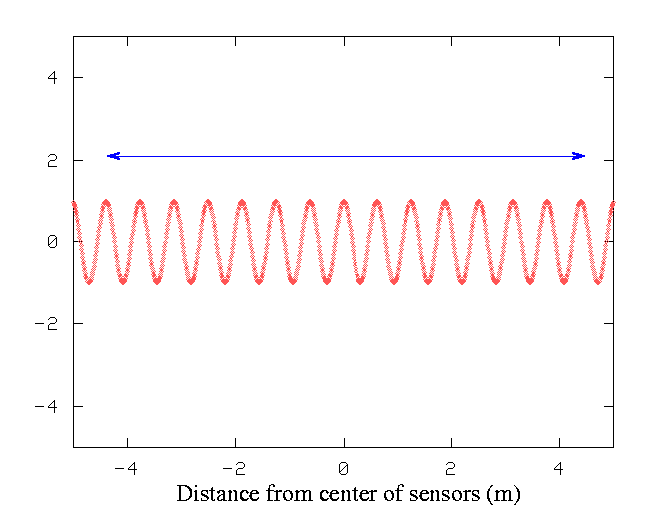
If we want to measure the wavelength of the wave accurately, we count the number of peaks between the start and end of our string of sensors, and divide by the distance. In the graph above, the units on the X-axis are meters.


  Q:  Using the measurements within the marked area,
      what is the wavelength of the earthquake wave?

The longer the stretch of waves we measure, the more accurately we can calculate the wavelength. Even if we make an error in the measurement of the position of the sensor at the left end of the string, it won't make much difference in the calculated wavelength, because we divide by a large number of peaks:

                       X(right sensor) -  X(left sensor)
        wavelength  =  ---------------------------------
                             number of peaks between

But what if we aren't interested in wavelength? What if we want to know the position of a wave? Suppose that the quake is very brief: it sends a short, sharp jolt through the ground.

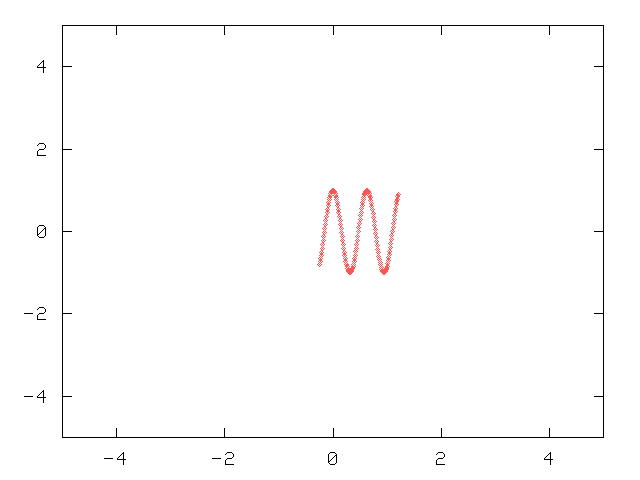
This compact wave has a pretty well defined position: only sensors within a meter or two register its effects. But measuring its wavelength isn't so easy: it has only two or three peaks, so any uncertainties in the positions of those peaks will cause relatively large uncertainties in the calculated wavelength.

So there appears to be a tradeoff: one can measure the wavelength precisely by looking at a long string of sensors -- but then the position of the wave is pretty loose. If we want to know the position of a sharp jolt, we pay attention only to a short string of the sensors -- but then the wavelength is hard to calculate. One can put the tradeoff into a mathematical form like so:


   (delta wavelength) * (delta position)  =  const

where delta is short for "uncertainty in the measurement of."

The usual form of this relationship replaces wavelength by its inverse, wave number k:

                              2 * pi
       wave number k  =  ----------------
                            wavelength

Stated this way, the relationship looks like:


   (delta wavenumber) * (delta position)  =  1

Wave packets

Here's another way to look at the tradeoff between wavelength and position. Start with a pure cosine (or sine) wave, like this:

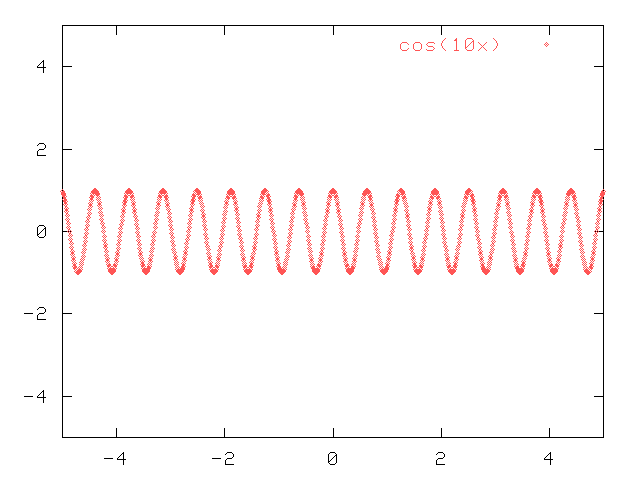
The amplitude of the wave is the same everywhere, as far as you look in both directions.

Now, the same is true for a cosine wave with a slightly different wavelength:

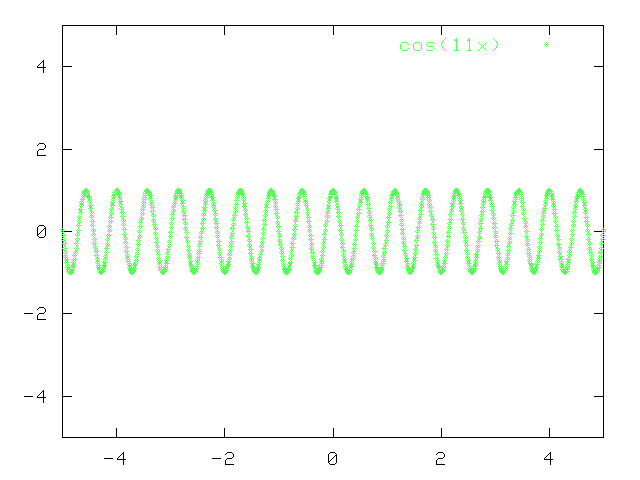
But what happens if you add together these two pure cosine waves with slightly different wavelengths?

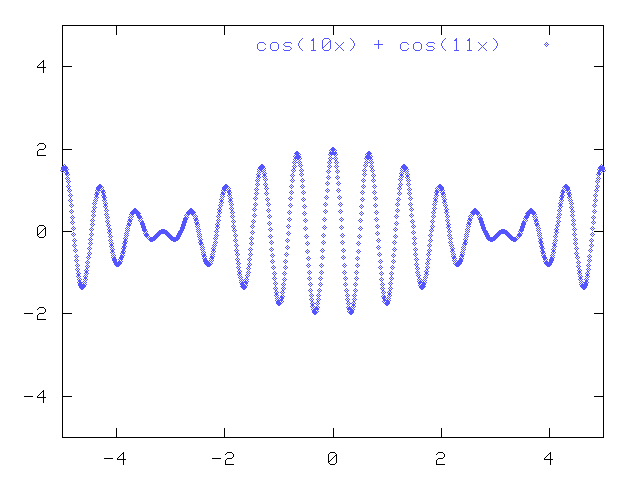
You get a complex wave which has a large amplitude over a restricted area, and smaller amplitude outside that area.

As you add more and more waves with slightly different wavelengths together, the resulting wave packet becomes more and more sharply defined:

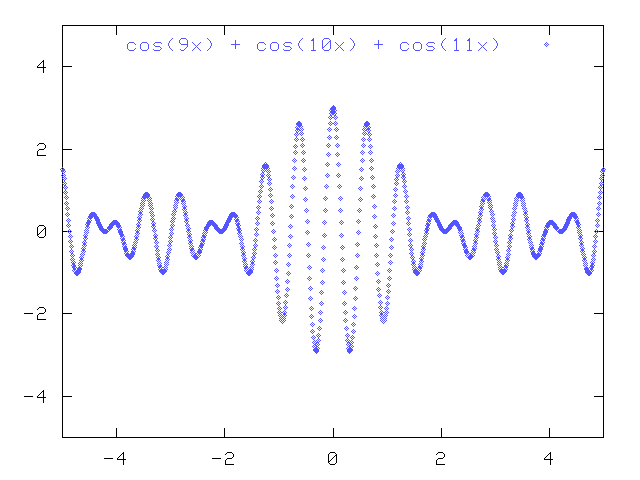
A packet like this does have a reasonably well defined position: it's the place where the amplitude of the complex wave is large.

On the other hand, if you look closely at the spacing between the peaks of this combination of different waves, you will find that it isn't constant anymore. You face a double whammy when trying the measure the wavelength of this packet:

the spacing between peaks varies
there aren't many peaks between the ends of the packet

Once again, there's a tradeoff: a wave packet with a mix of wavelengths has a well defined position (but not wavelength), whereas a pure wave has a well defined wavelength (but not position).

Heisenberg's application to waves of matter

De Broglie showed that particles of matter exhibit wave-like properties under certain circumstances, with wavelengths which depend on the particles' momentum:


                               h
           wavelength  =   -----------
                            momentum

Heisenberg realized that this meant that particles -- like any waves -- would have to obey the tradeoff between wavelength and position. Since wavelength and momentum are simply connected, this meant that one could state the tradeoff as


   (delta momentum) * (delta position)  =  const

With a careful analysis, Heisenberg was able to show that the constant factor included Planck's constant:


                                              h
   (delta momentum) * (delta position)  =  --------
                                            2 * pi

So Planck's constant doesn't only govern the "graininess" of energy levels inside atoms, or the "graininess" of photon energies. It also describes the the "graininess" of our ability to measure the properties of particles. Remember, though, that Planck's constant is a small number, which means that this graininess only appears when one looks very, very closely at very, very small phenomena.

For more information

Read all about Werner Heisenberg's life and times at this AIP History site.