The Simple Harmonic Oscillator

Your introductory physics textbook probably had a chapter or two discussing properties of Simple Harmonic Motion (SHM for short). Your modern physics textbook mentions SHM, too. In fact, if you open almost any physics textbook, at any level, and look in the index under "Simple Harmonic Motion", you are likely to find a number of references. What's so great about Simple Harmonic Motion?

The answer is two-fold:

It's very common, in all different sorts of situations
It's easy to describe theoretically

Here are just a few examples of SHM:

Image courtesy of How Stuff Works

This Les Paul guitar can be purchased from Gibson Guitars

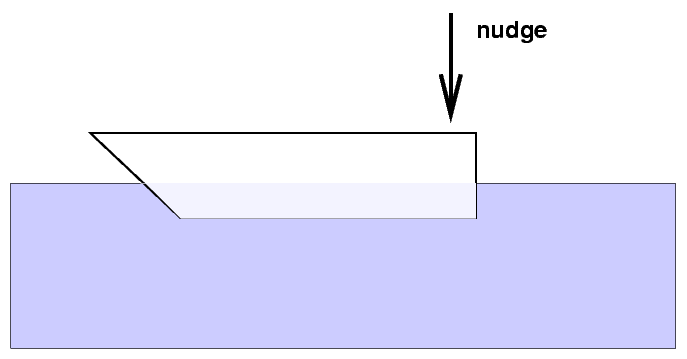
Push down slightly on a floating object and watch it bob up and down ...

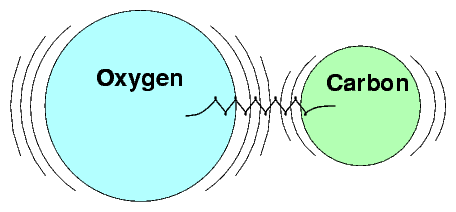
SHM in terms of force, or in terms of potential

We can describe the conditions under which SHM will occur in several ways.

In terms of forces, SHM occurs when an object experiences a linear restoring force when displaced from its rest position. In other words, a force which

pushes it back towards the rest position (opposite to the displacement)
grows larger as the displacement grows larger, in a linear fashion: twice the displacement means twice the force, three times the displacement means three times the force

Mathematically speaking,

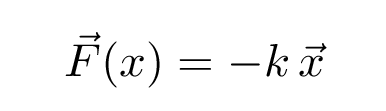
In terms of potential energy , SHM occurs when an object sits in the middle of a quadratic potential. Mathematically speaking,

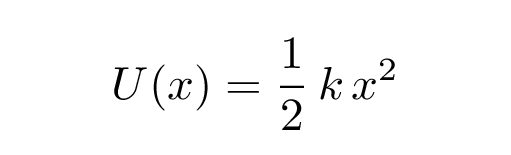
We can also look at things graphically. If we make a plot showing position along the horizontal axis and potential energy along the vertical axis, we see a familiar form:

The classical view of SHM

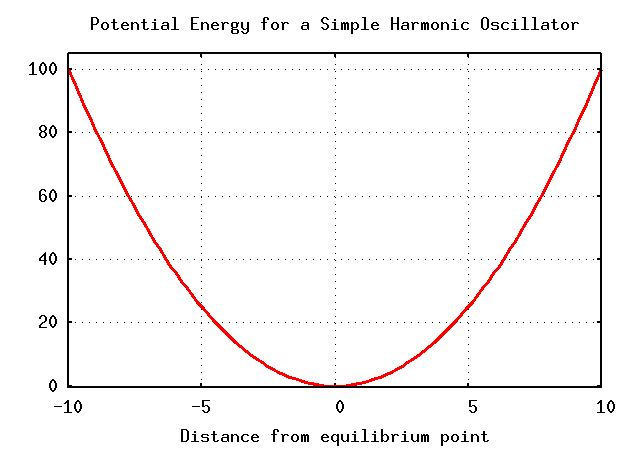
The classical example of SHM is a spring of force constant k with a mass m attached. If we displace the mass from its equilibrium position by a distance A and then release it at time t = 0, then the mass oscillates in a simple fashion:

As the mass moves, it exchanges kinetic energy for spring potential energy, but the sum of the two remains fixed:

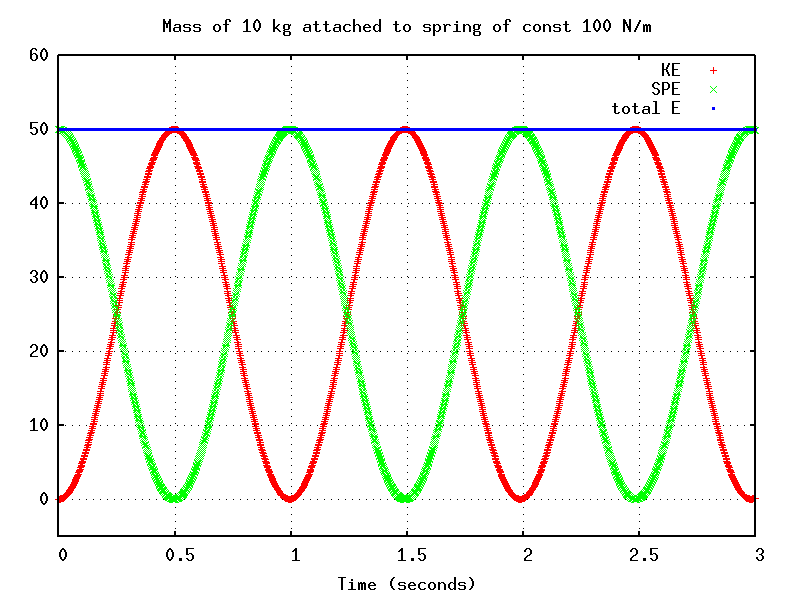
The total energy of the system depends on the amplitude A:

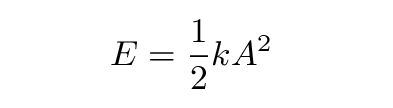
Note that we can give the system any energy we wish, simply by picking the appropriate amplitude.

The frequency of oscillation, on the other hand, does NOT depend on the amplitude of oscillation; that's why we use pendula to drive clocks, of course. The frequency depends only on the force constant of the spring and the mass:

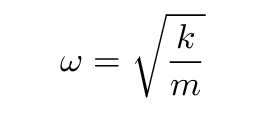
Suppose that we were to make a movie an oscillating spring over many cycles. At which position(s) would the mass appear in the most frames of the movie? In other words, which is the most probable position to find a mass attached to a moving spring?


  Q:  Where is the mass most probably to be seen?

       a) near the equilibrium point, in the middle
       b) near the outer limits of its motion
       c) equally likely everywhere

Well, the faster the mass moves through some particular location, the less likely we are to find it at that location. The velocity of the mass is largest as it moves through the equilibrium position, and slowest near the outer reaches of its motion (the turning points):

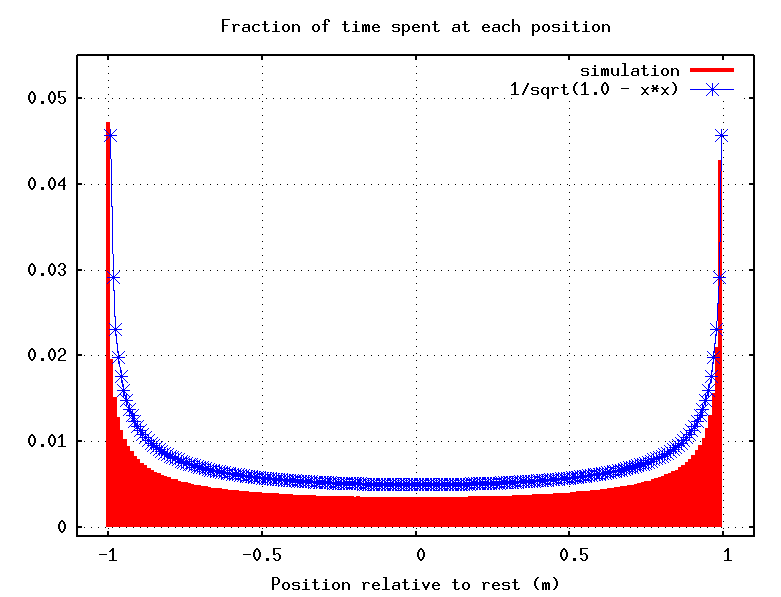
So we are most likely to find the mass at the limits of its motion, and least likely to find it near equilibrium. This doesn't depend on the amplitude of the oscillation, so the answer is the same for any energy.

The quantum view of SHM

Let's now look at the situation through the lens of Mr. Schroedinger's equation. Starting with the familiar 1-D time-independent version of the equation,

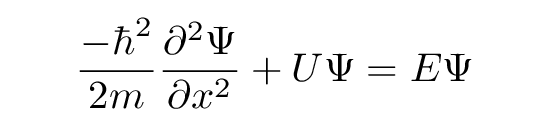
we insert for the potential energy U the appropriate form for a simple harmonic oscillator:

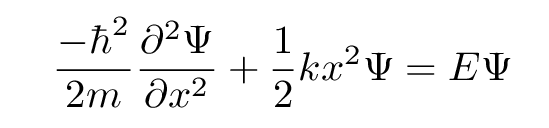
Our job is to find wave functions Ψ which solve this differential equation. Ugh.

A good way to start is to move the second derivative over the to left-hand side of the equation, all by itself, and put all other terms and coefficients on the right-hand side.



   Q:  Re-arrange the equation so that it looks like this:

You should end up with this:

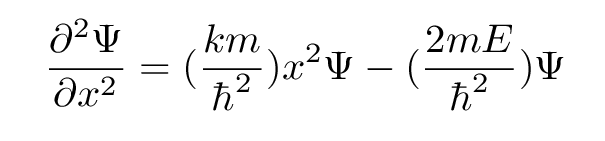
Hmmmm. The second derivative involves both the original function Ψ and also a term with Ψ multiplied by x². We need to find a function which will solve this differential equation. When in doubt, guess.



  Q:  Which of the following wave functions will solve
      this particular differential equation?

Yup. The final of the three guesses above does the trick. Its second derivative with respect to x is

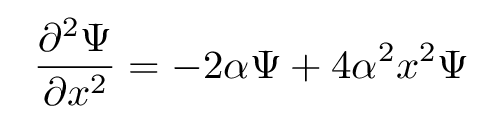
Aha. Now, looking back at the Schroedinger equation for this choice of potential, we see

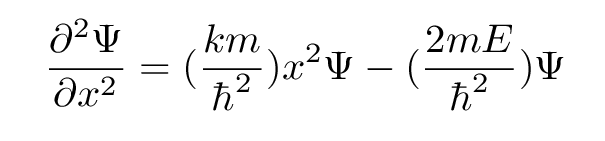
In both cases, the second derivative of the function Ψ involves two terms:

one term has only a constant coefficient
one term has a factor of x² as well

If we want to make our guess solve the Schroedinger equation for a quadratic potential, at all positions of x, we need to match up our two terms to the Schroedinger equation's two terms.



    Q:  Solve for the value of "alpha" in our function
        by matching the terms with factor x².


    Q:  Then figure out the energy E by matching the 
        terms with constant coefficient.

You should end up with

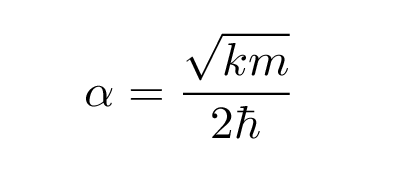
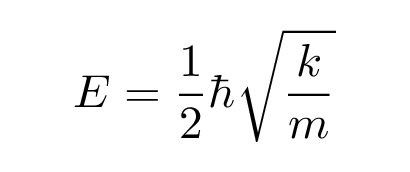
Fine -- but what does the solution mean?

Let's take a step back and look at the big picture. We have a quadratic potential energy function around some equilibrium point.

We can solve Schroedinger's equation in this situation by picking a wave function like this:

where the coefficient alpha -- which must have units of inverse distance squared -- is given by

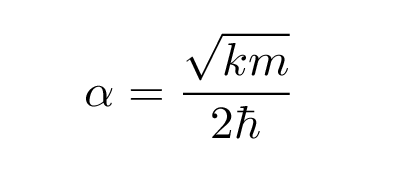
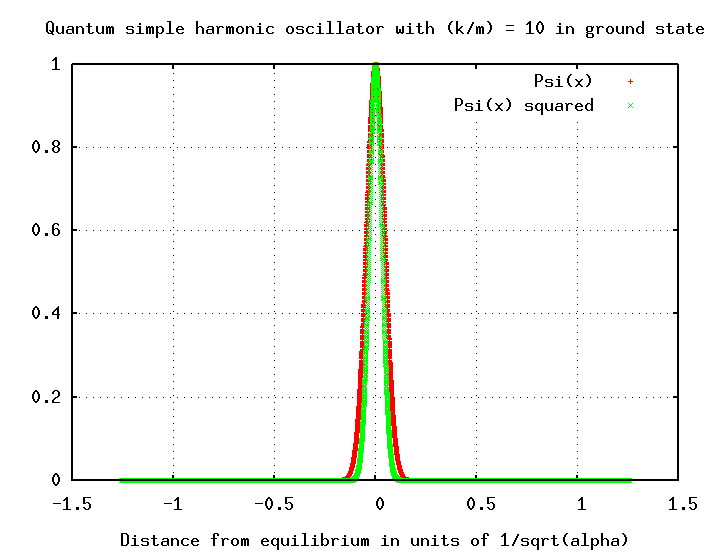
Hmmmmm. This wave function falls off VERY quickly as a function of distance x from the equilibrium point.

The rough amplitude of the oscillations must have units of length; we can get a length from alpha like so:

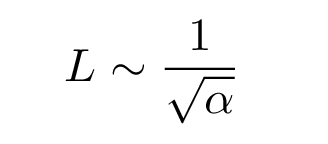
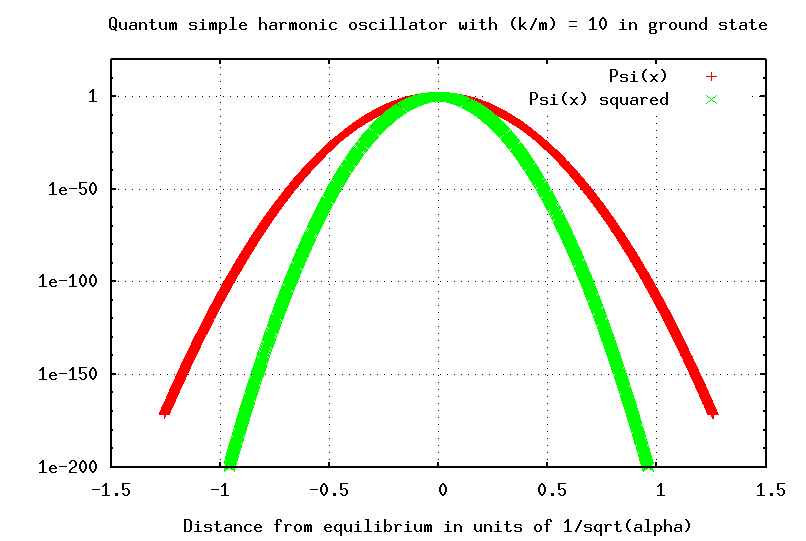
Note that in the quantum world, this length isn't a simple, fixed thing. The particle is EXTREMELY unlikely to be found as far from equilibrium as this length L; it is much more likely to be within, oh, 0.1 L of equilibrium. The most probable location of the quantum SHO is exactly at the equilibrium position -- which is exactly opposite to the case of the classical SHO. On the other hand, if you look at the logarithmic version of the probability graph, you can see that there is a non-zero chance that the particle will be even more than L away from equilibrium.

The frequency of oscillations is -- just as in the classical case -- given by

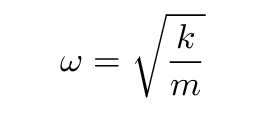
Wait a second -- that looks familiar. The solution to the Schroedinger equation demands that the energy of the particle be

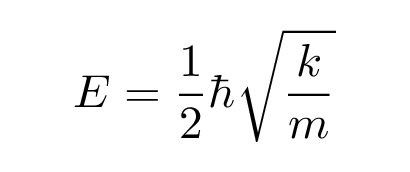
Putting this together, it seems that the energy of the quantum oscillator -- UNLIKE the classical one -- does depend on its frequency:

Does this relationship between energy and frequency of oscillation remind you of anything else? Perhaps something that Mr. Planck stated ....

Beyond the ground state

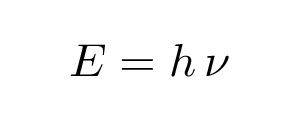
Our solution to the Schroedinger equation above was just one particular solution. There are a whole family of solutions, all of which involve the same exponential of x², but including increasingly complicated polynomials of x. For example, the ground state solution we found was

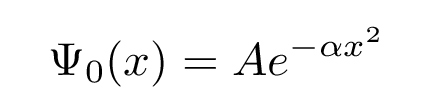
with energy

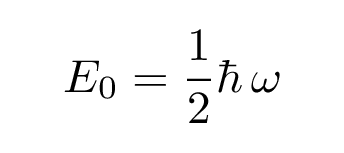
The next solution, for the first excited state, has the form

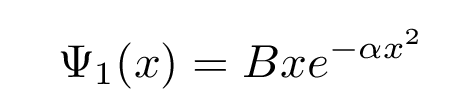
with the same alpha as before; but the energy for this solution is larger:

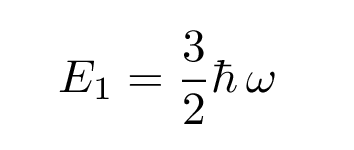
There are a series of solutions for increasingly excited states, with energies which have the general form

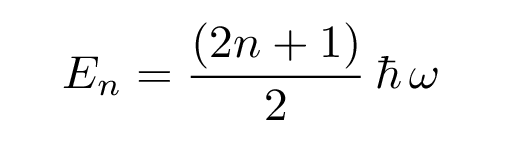
Note the difference between the energy levels for the quantum solutions to a particle in a potential with infinitely steep sides ("particle in a 1-D box") and a potential with sloping sides ("quadratic well"):

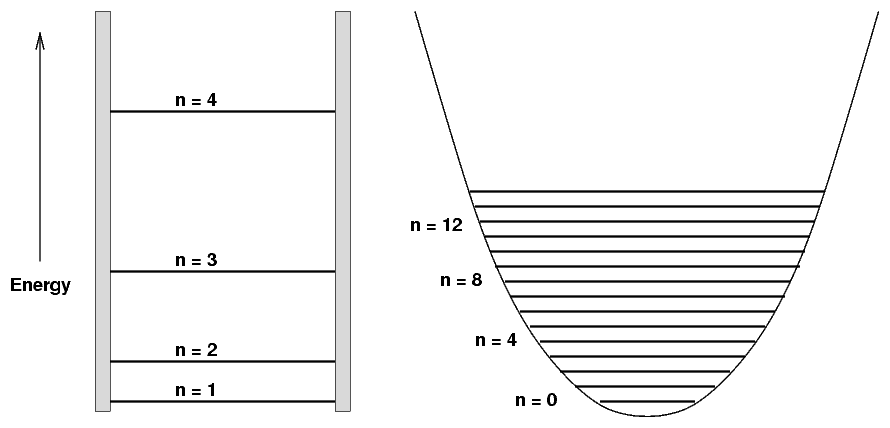
That means that spectrum of a molecule which behaves like a simple harmonic oscillator -- such as water or carbon monoxide -- will show absorption bands featuring many lines at (almost) equal intervals of wavelength. For example, if we look at sunlight passing through carbon dioxide in the Earth's atmosphere in the near-infrared, we see

For more information

The Foucault Pendulum is explained by Joe Wolfe of the University of New South Wales.
Minimizing Strong Telluric Absorption in Near Infra-red Stellar Spectra is a paper describing how one can get RID of the absorption bands due to CO and water in the Earth's atmosphere.
Resolution of the Telluric Bands ω_{1} and ω_{2}, an article by Arthur Adel published in ApJ in 1943, shows spectra taken with photographic plates.