Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
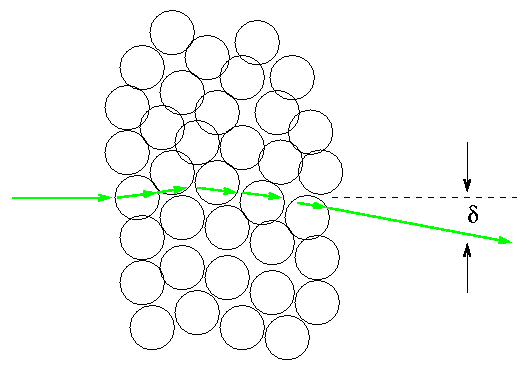
So, if the positive charge within an atom is spread out evenly throughout its entire volume, as it Thomson's plum-pudding model, one can calculate the typical angle by which an alpha particle might be deflected in an interaction with a single atom:
theta = 0.01 degree
As an alpha particle moves through a thin section of foil, it encounters many atoms. Each atom gives it a small deflection in some random direction. After it comes out of the foil, the alpha particle has some overall deflection delta which is the sum of all the small deflections.
In order to bend by a large angle, say, 90 degrees, all the small deflections would have to be in the same direction: all "to the left", for example. That's not very likely. If there's a 50% chance that each deflection goes "to the left" versus "to the right", what are the chances that consecutive deflections add up to 90 degrees?
Q: How many consecutive deflections in a row
would it take to add up to delta=90 degrees overall?
Q: What are the odds that this happens to one
particular alpha particle?
In the early twentieth century, English physicist Ernest Rutherford ran a lab in which experiments of all kinds were performed. One of his assistants, Hans Geiger, investigated scattering of alpha particles by thin films of different metals. In this paper from 1910,
Geiger reports on his work. He set up an evacuated glass tube with a radioactive material (radium) coating the walls of the tube at one end, and a flourescent screen at the other end:
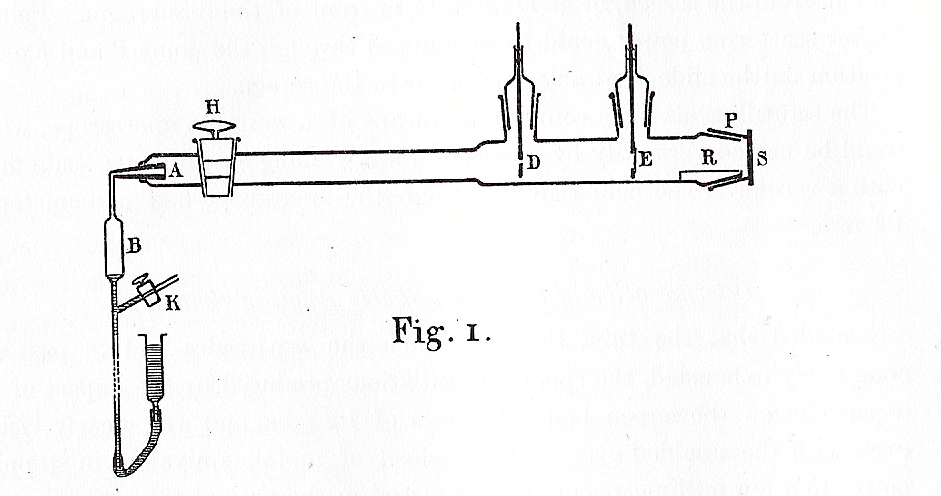
The conical section of glass, A, was coated with radium. After about fifteen minutes, the most active radioactive materials disappear, leaving only a single isotope which emitted alpha particles. These flew down the length of the tube, through a small diaphragm D, then struck a foil at E. At the very end of the tube was a flourescent screen S, which would light up with a tiny flash whenever an alpha particle struck it. Geiger would very carefully count the number of flashes at various points on the screen, and derive the angle through which the alpha particles had been deflected by the screen.
Now, Geiger used the Thomson model to interpret his results. He found a typical scattering angle which was indeed small:
But there was one little surprise: he occasionally saw a flash of light on a screen placed on the OTHER side of the foil, meaning that an alpha particle had bounced BACKWARDS.
He determined that about 1 in 8000 alpha particles bounced backwards. But if the typical scattering angle is just 1/200 of a degree, then it should take a number of consecutive "left-hand" turns N given by
90 degrees
N = ------------- = 18,000
1/200 degree
If there's a 50% chance of scattering to the left or the right each time the alpha encounters an atom, the probability of 18,000 consecutive left-hand turns is
-18,000 -6,000
prob P = 2 = 10
which is a lot smaller than 1 in 8000. A LOT smaller. A REALLY BIG LOT smaller!
In the words of Rutherford,
It was quite the most incredible event that ever happened to me in my life. It was as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you.
So what was going on? The Thomson model can't explain it. In the old-fashioned tradition of being cautious (which doesn't exist much anymore -- it doesn't get press), Geiger writes:
But he (and Rutherford) did have an idea ... one that they published three years later, after an exhaustive series of similar experiments.
Rutherford realized that a bunch of weak scattering events would never lead to the observed frequency of angles greater than 90 degrees. For one thing, the thin foils he and his colleagues were using were only several hundred atoms thick; there just wasn't time for an alpha particle to encounter the thousands of atoms needed to bend its path by large angles.
Perhaps each alpha underwent just one scattering event -- but one which could sometimes be very strong.
The experiments showed several relationships between the number of alpha particles scattered at some angle theta and other quantities: the type of material in the foil, its thickness, the kinetic energy of the incoming alpha particles, etc. Rutherford worked out a model which could explain all the correlations.
From "The Scattering of alpha and beta Particles by Matter and the Structure of the Atom," Philosophical Magazine, vol. 21, p. 669 (1911)
In this new model, all the positive charge of the atom was concentrated in a tiny point at the center; around it was nearly empty space, inhabited by the electrons alone. As Rutherford put it, the atom wasn't a plum pudding; it was more like
... like a few flies in a cathedral ...
The crucial point was the very small size of the "nucleus": since all the positive charge was concentrated in so small a volume, the projectile could OCCASIONALLY come very, very close to it; so close that the electric force would be large enough to push the projectile by a very large angle, maybe even backwards.
Let's use the impulse approximation again to get a feeling for what's happening.
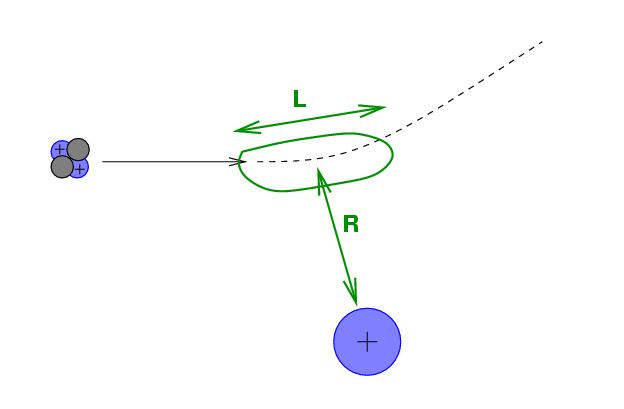
If the alpha particle approaches the nucleus to a minimum distance R, then the impulse imparted to the alpha by the electric force is roughly the force at closest approach multipled by the duration of the passage:
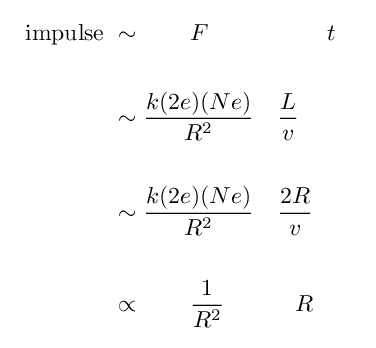
Q: What happens to this impulse as the
distance R decreases?
Q: What is the rough size of an atom?
Q: What is the rough size of a nucleus?
Q: How much stronger is the impulse if the
positive charge is compressed within
the nucleus, rather than being spread
throughout the entire volume of an atom?
Using his model, Rutherford derived two formulae which described the behavior of alpha particles as a function of the other variables in the experiment. First, he could determine the impact parameter b of an charged particle which was scattered by an angle theta:
Given the Coulomb force constant ke, the charge z (in electron units) on the projectile, the charge Z (in electron units) on the atom, and the kinetic energy K of the projectile, Rutherford's model yields:
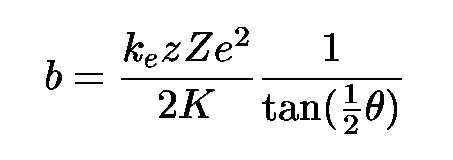
One can use this formula to derive equation 6.15 in your textbook. That derived relationship concerning the fraction of particles scattered by more or less than a particular angle will come in handy on this week's homework assignment.
If one measures the fraction of particles which are scattered by various angles as they pass through a foil, one can work out the fraction of the cross-section of an atom which is occupied by the nucleus. In other words, one can measure the size of the nucleus!
Rutherford's model also makes a series of predictions between the fraction of particles scattered at a particular angle and a number of quantities involved in the experiment:
Rutherford was able to put all this information into a single complicated formula:
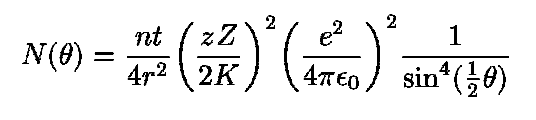
Using this formula, and the experimental results of Geiger and Marsden, Rutherford was able to figure out the approximate electric charge of the nucleus of a gold atom:
What's the currently accepted value for the electric charge in a gold nucleus?
One of the somewhat surprising results of the experiments was that the variations in angle didn't run exactly as one might expect with elements of increasing atomic weight. Naively, one might expect that an element with an atomic weight of N might have N positive charges at its center. However, as Geiger and Marsden write in the conclusion to their paper The Laws of Deflexion of alpha Particles through Large Angles, Philosophical Magazine, vol 25, p. 604 (1913):
Can you explain why the number of positive charges N in a nucleus was only about HALF the atomic weight?
Quite an impressive amount of information, no? As an analogy, imagine trying to discern the internal structure of an automobile from a distance of several hundred yards by shooting a high-powered rifle at it.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.