Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Back in high school physics or chemistry class, you probably learned about several Conservation Laws:
2
E = m c
it turns out that mass can be converted to energy,
and energy converted to mass.
In these circumstances, the laws change a bit:
As you saw in Homework 1, an isolated neutron has a half-life of only minutes. If you watch one carefully, you'll see it disappear in a flash of radiation, and, in its place, several particles will appear:
Does this reaction conserve mass? Does it conserve energy? Let's see:
particle mass (kg) mass (MeV/c^2) --------------------------------------------------- neutron 1.6749 x 10^(-27) proton 938.27 electron 9.1094 x 10^(-31) anti-neutrino 0 ---------------------------------------------------
So, if we add up all the mass before and after, we get
before after
1.6749 x 10^(-27) kg 1.6735 x 10^(-27) kg
That leaves a difference of 0.0014 x 10^(-27) kg. Whoops. Does that mean that this reaction can't take place? No! It just means that the reaction products -- the proton, electron, and neutrino -- must carry with them a little extra energy in kinetic form. How much?
Q: How much kinetic energy must the
proton, electron and neutrino
carry away with them?
Okay, so the particles created in the decay must carry away some kinetic energy. Can they fly away from the site of the decay like this?
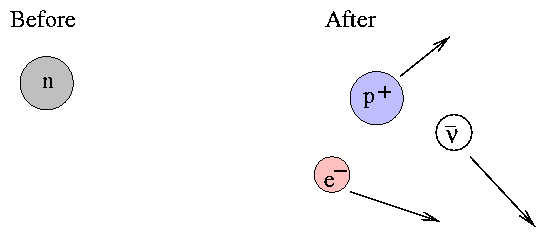
No! This might conserve mass-energy, but it certainly does NOT conserve momentum. Instead, the particles might move something like this:
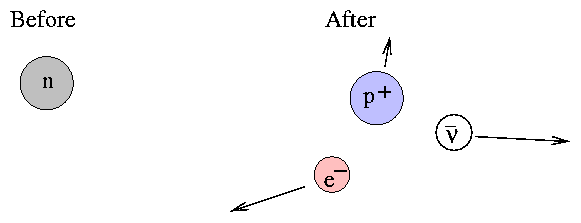
Think about it: in this situation, you must conserve mass-energy, and conserve momentum; that gives you two equations. You can solve for at most two unknowns. In the picture above, in which the proton, electron and anti-neutrino all fly away from the decay site? how many unknowns are there? Nine, for the components of each particle's velocity in the x, y and z directions. It would appear that the solution is not unique -- there might be many combination of different velocities among the three decay products.
If someone gives you enough additional information, you might be able to use just the conservation of momentum and mass-energy to solve for the remaining unknowns. For example, consider this version of the decay: the proton sits motionless, the anti-neutrino shoots off to the right, and the electron flies off to the left:
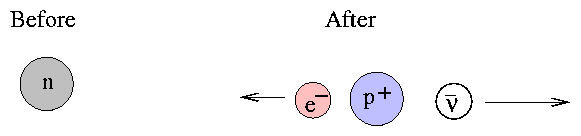
It turns out that there are now only two unknowns:
These two unknowns ARE determined uniquely from the two conservation laws. The problem is left as an Extra-Credit exercise for the reader.
You've probably heard of anti-matter in science-fiction stories, but it's real. Each particle (proton, electron) has a corresponding anti-particle (anti-proton, anti-electron) which has the same mass, but opposite charge. If a particle meets its anti-particle, the two annihilate: they disappear into a burst of energy.
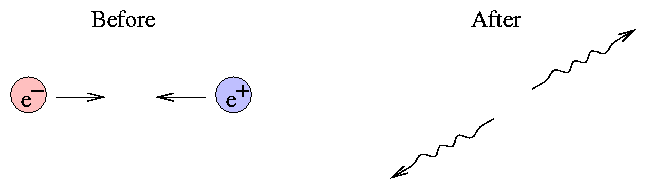
Q: If two identical gamma rays are produced,
how much energy does each have?
This works both ways, of course:
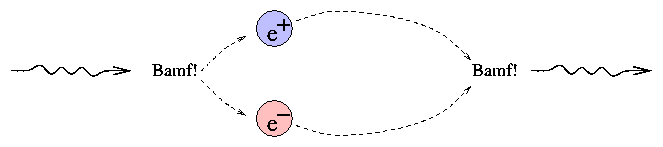
Don't forget to include the kinetic energy of the input particles, if they are moving at relativistic speeds. This can be the dominant form of energy in some cases. For example, the Tevatron at Fermi National Accelerator Laboratory accelerates protons and anti-protons to extremely high speeds around a giant ring
then smashes them together and looks very carefully at the resulting spray of particles and energy.
Q: What is the rest energy of one proton
and one anti-proton together?
Express your result in Joules and
in MeV.
The goal of the Tevatron is to look for the
mysterious
Higgs Boson,
a particle which (if it exists) would have profound implications
for subatomic physics.
The problem is -- it's massive. Really massive.
Current estimates suggests that its rest mass lies somewhere
between 100 Gev/c^2 and 1000 GeV/c^2.
That means that the proton and anti-proton must both
be moving VERY close to the speed of light when
they collide in order to release enough energy to create
a Higgs boson.
Q: To what factor of gamma must the
proton and anti-proton be accelerated
in order to create a Higgs boson?
Q: To what fraction of c does this correspond?
Just what the heck is the "Higgs boson?"
Some physicists make a big deal over it ....
In response to a challenge issued by the UK Science Minister, William Waldegrave, 'What is the Higgs boson, and why do we want to find it?' David Miller of the Department of Physics and Astronomy, University College, London, came up with an excellent analogy that starts like this:
Imagine a cocktail party of political party workers who are uniformly distributed across the floor, all talking to their nearest neighbours. The ex-Prime Minister enters and crosses the room. All of the workers in her neighbourhood are strongly attracted to her and cluster round her. As she moves she attracts the people she comes close to, while the ones she has left return to their even spacing. Because of the knot of people always clustered around her she acquires a greater mass than normal, that is she has more momentum for the same speed of movement across the room. Once moving she is hard to stop, and once stopped she is harder to get moving again because the clustering process has to be restarted.
You can read the rest of his reply, as well as other winning responses to the challenge.
The standard way to describe the explosive yield of a bomb is in terms of the mass of TNT which would be required to produce the same explosive energy. By convention,
9
1 metric ton of TNT --> 4.2 x 10 Joules
The bomb dropped on Hiroshima (called "Little Boy") produced about E = 13 kilotons of energy.
Q: What mass of matter was converted to energy
by this weapon?
Q: The total mass of the bomb was about 4000 kg.
What fraction of the bomb's entire mass was
turned into energy? (This might be called
the "efficiency" of the device)
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.