Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
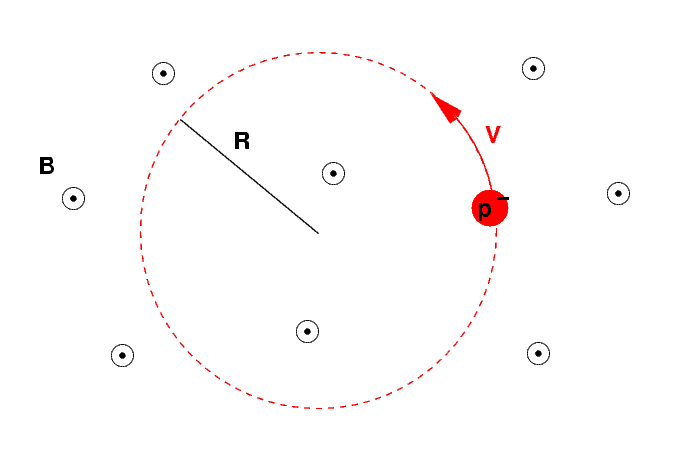
One way to measure the velocity and/or energy of a particle is to send it into a region containing a strong magnetic field. Any particle with charge will feel a force due to the combination of its charge, its velocity, and the magnetic field:
F = q (v x B)
As a result, the particle will move in a circle (or a helix, but let's stick with two dimensions for now).
The radius R of the circle can be determined from the particle's mass, and charge, and velocity, and the strength of the magnetic field.
Q: Derive a formula for the radius R
of the circle.
In practice, physicists shoot particles of unknown speed into a magnetic field, observe the size of the curved paths they follow, and then derive the particles' speed; or, equivalently, the particles' energy.
Q: Re-arrange the above formula to solve
for velocity V.
Okay, let's try using this relationship.
Physicists observe that an anti-proton moves in a circle of radius R = 0.0626 m when placed in a magnetic field of strength B = 0.5 Tesla.
Q: What is the speed of the anti-proton?
What is the kinetic energy of the anti-proton?
Physicists observe that another anti-proton moves in a circle of radius R = 12.5 m when placed in a magnetic field of strength B = 0.5 Tesla.
Q: What is the speed of this anti-proton?
What is the kinetic energy of this anti-proton?
The answer, part 1
The answer, part 2
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
