Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
So, Planck could
But in some ways, he didn't really believe in the quanta required by his explanation of the blackbody spectrum. He didn't see the consequences of discrete energy packets .... but someone else did. A young man named Albert Einstein. Einstein saw that Planck's idea would explain some mysterious properties of experiments in which light shone on metal electrodes.
At the turn of the century, physicists who experimented with electricity had noticed something about the interaction of light, metals, and electric current. One of the most thorough accounts of such experiments was written by Lenard, in Annalen der Physik, vol. 4, p. 149 (1902) (written in German, in which I am not fluent, alas).
One of Lenard's experiments involved shining light on a piece of metal which was part of a broken circuit:
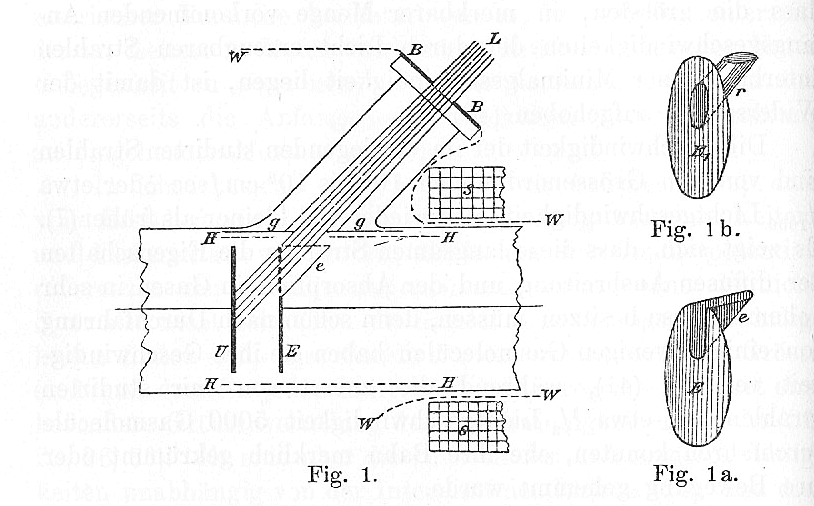
In this figure, a circuit connects metal plates U and E, which are separated in a vacuum by a small gap. One can set a voltage across the plates by modifying the circuit. Light from source L shines onto plate U.
The light waves may knock some electrons out of the plate U, causing them to fly across to the other plate E. These electrons complete the circuit. One can use an ammeter to measure precisely how many electrons jump from one plate to the other.
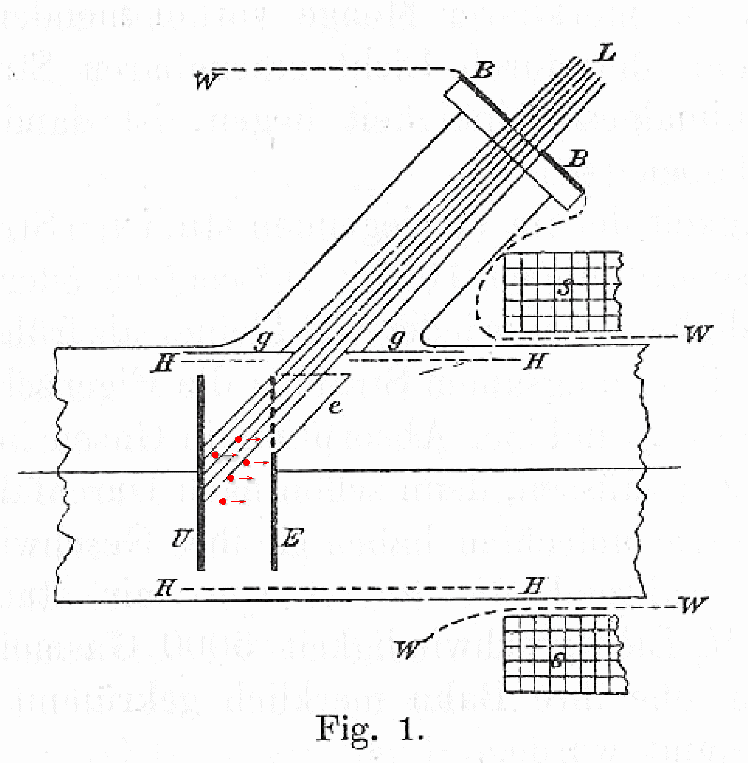
This current of electrons produced by light is called the photoelectric effect.
Now, if one arranges the voltage between the plates so that the "source" plate U is negative, and the "receptor" plate E is positive, the electrons are pushed away from the source and towards the receptor -- which helps the current to flow. But if one makes the "source" positive, and the "receptor" negative, then the voltage across the plates pushes the electrons BACK to the source.
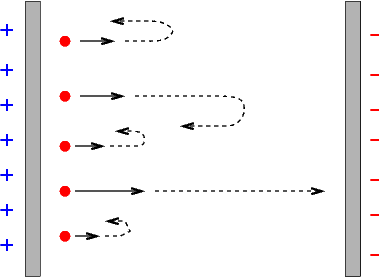
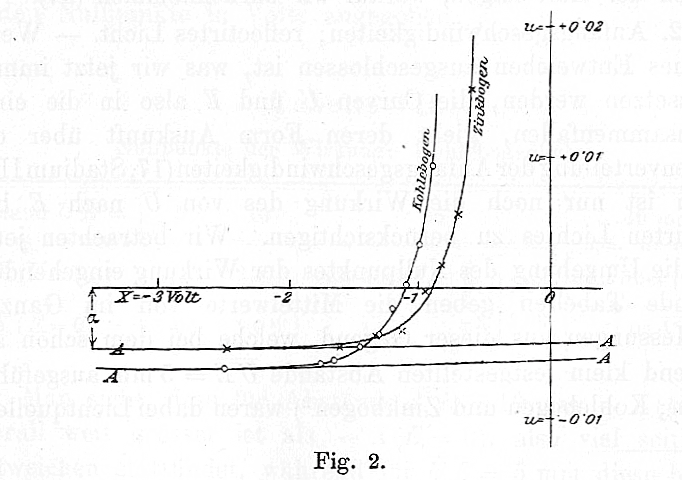
If one starts with zero voltage across the plates, then some current will flow when the light is turned on: electrons knocked off the "source" plate with any speed will eventually reach the "target" plate. But if one gradually increases the voltage difference, fewer and fewer electrons will make the journey, and eventually the current disappears. In this figure from Lenard's paper, the potential voltage is plotted on the horizontal axis, and the current on the vertical axis. There is a small offset from zero current due to Lenard's apparatus.
What's going on? As each electron moves from the positive "source" plate towards the "receptor" plate, it must do work against the electric field; it exchanges kinetic energy for electric potential energy. At some point, it loses all its kinetic energy ... and so stops moving forward. Now, when the electrons are knocked free, some have a lot of kinetic energy, others only a little. The ones with the most kinetic energy are the last ones to stop reaching the "receptor" as we increase the voltage difference. We can calculate this MAXIMUM kinetic energy among the photo-electrons:
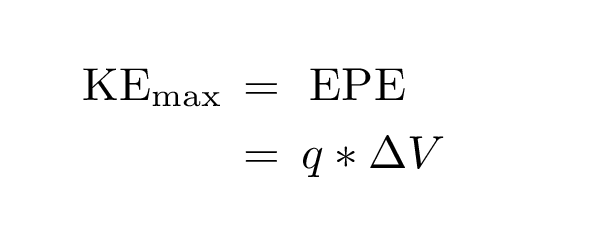
(Fortunately, these electrons aren't moving at relativistic speeds!)
In the figure from Lenard's paper shown above, what was the maximum kinetic energy of the photoelectrons?
Now, one might try to explain this photoelectric effect with waves of light: light waves impinge on the source plate. They give energy to electrons on the plate. The electrons fly off the source plate to the receptor. The wave theory predicts several things:
Careful measurements in the lab, however, showed that these predictions were wrong, wrong, wrong.
Planck's explanation of the blackbody spectrum was published in 1900. Five years later, Einstein published a paper (in the very same issue as his famous paper on relativity) which used Planck's idea of quanta to explain the photoelectric effect's quirks. He wrote:
In accordance with the assumption to be considered here, the energy of a light ray spreading out from a point source is not continuously distributed over an increasing space, but consists of a finite number of energy quanta which are localized at points in space, which move without dividing, and which can only be produced and absorbed as complete units.In other words, Einstein proposed that light behaved not like a wave, but like a particle: the photon (a word coined in 1926 by G. N. Lewis).
How does this explain the observed photoelectric phenomena?
And yes, this implies that the time it takes for an electron to lose the energy gained in one absorption is much smaller than the interval between absorptions. Under ordinary circumstances, it is.
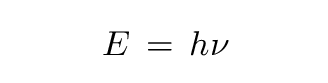
below some critical frequency, no photon has enough energy to knock an electron free.
Moreover, Einstein's theory was able to make one very strong prediction: the maximum energy of ejected electrons should increase linearly with frequency of the applied light. Again quoting Einstein,
... We shall assume that in leaving the body, each electron must perform an amount of work P characteristic of the substance. The ejected electrons leaving the body with the largest normal velocity will be those that were [located exactly on] the surface. The kinetic energy of such electrons is given by h*ν - P.If the body is charged to a positive potential V0 and is surrounded by conductors at zero potential, and if V0 is just large enough to prevent the loss of electricity, it follows that
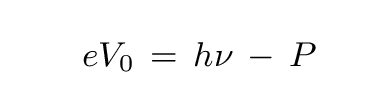
where e is the electronic charge ...
It seems simple enough to test this idea: shine light of various frequencies on a source plate, and measure the voltage V0 which just stops the current from flowing. And yet no one had ever tried it:
At the time at which it was made, this prediction was as bold as the hypothesis which suggested it, for at that time there were available no experiments whatever for determining anything about how the positive potential V necessary to apply to the illuminated electrode to stop the discharge of negative electrons from it under the influence of monochromatic light varied with the frequency ν of the light, or whether the quantity h to which Planck had already assigned a numerical value appeared at all in connection with photo-electric discharge.
Millikan, The Electron, 1917
This was exactly what Robert Andrews Millikan (yes, that Millikan) did. In an experiment performed in 1915 (and published in Physical Review,, vol VII, p. 362 (1916)), he set up a system in which he could measure the photoelectric effect accurately from freshly-scraped surfaces of alkali metals. The glass vessel shown below was evacuated; one of the metal samples mounted on the wheel W at the center was rotated to bring it next to the knife K, which scraped it clean; then the sample was rotated 180 degrees to face light shining through aperture O.
Millikan's data is shown below (I've wiped clean his calculation of the value of h from the graph). He shone light of various frequencies (plotted on the horizontal axis; note the factor of 10 to the 13'th power!) on the metal plate, and determined the minimum voltage (plotted on the vertical axis) necessary to halt the induced current.
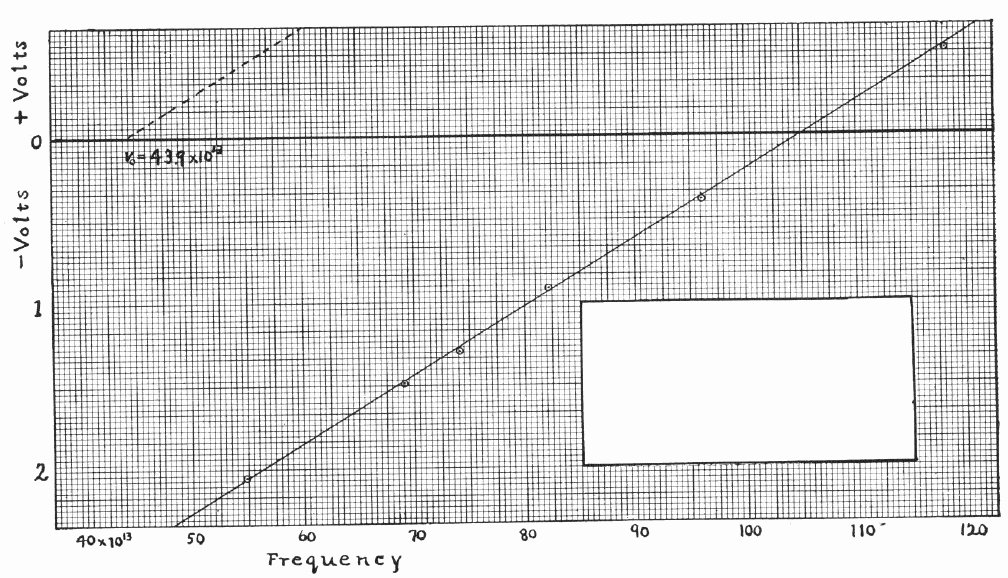
Does the stopping voltage increase linearly with frequency of the incident light?
What is the value of Planck's constant h based on this data?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.