Muons from cosmic rays and time dilation

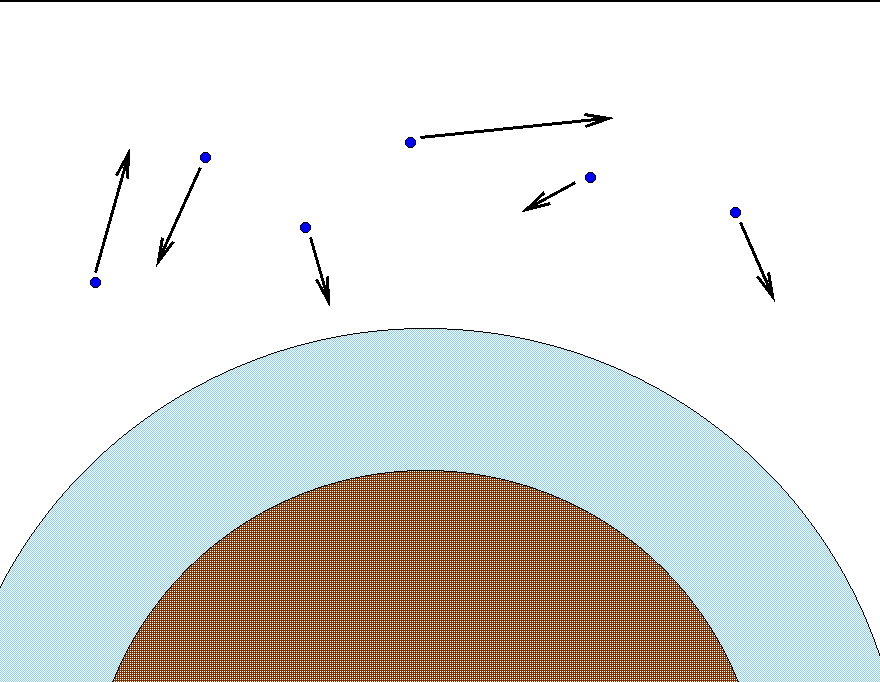
Space around the Earth is not quite empty. There are a number of energetic particles, mostly protons, electrons, and helium nuclei, flying this way and that. Physicists give these particles the name cosmic rays (yes, they are particles, not electromagnetic radiation, but such is historical tradition ...). Some are created by the Sun, but others have been travelling through interstellar space for eons and are just passing through the solar system.

Occasionally, one of these protons happens to fly straight into the Earth's atmosphere at very high speed.

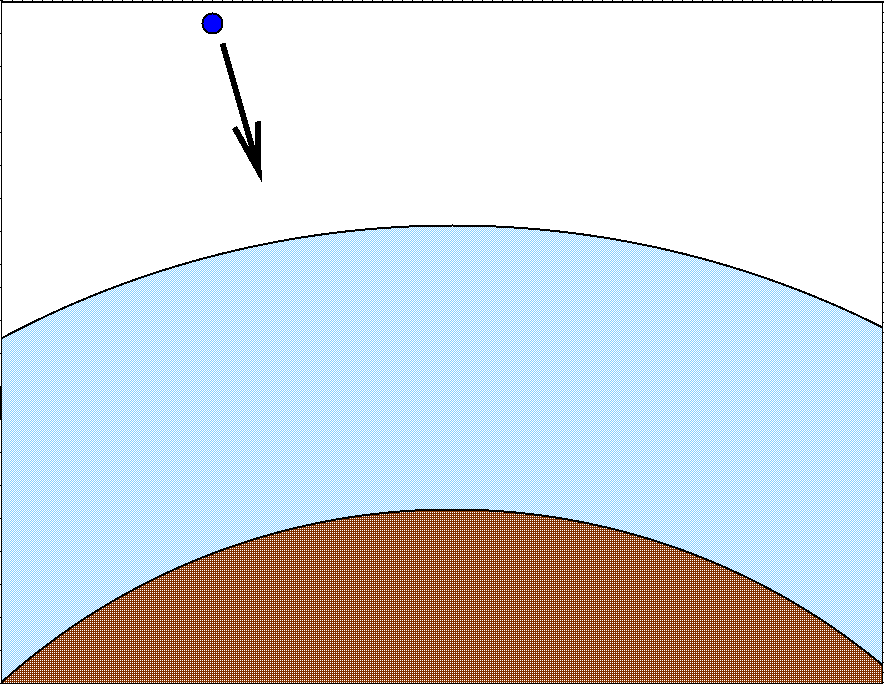
When it hits air molecules in the upper atmosphere, much of the proton's enormous kinetic energy is converted into a flurry of new particles (we'll discuss this at greater length later in the course). These new particles inherit much of the kinetic energy and momentum of the proton, and so zoom downwards through the atmosphere at very high speeds.

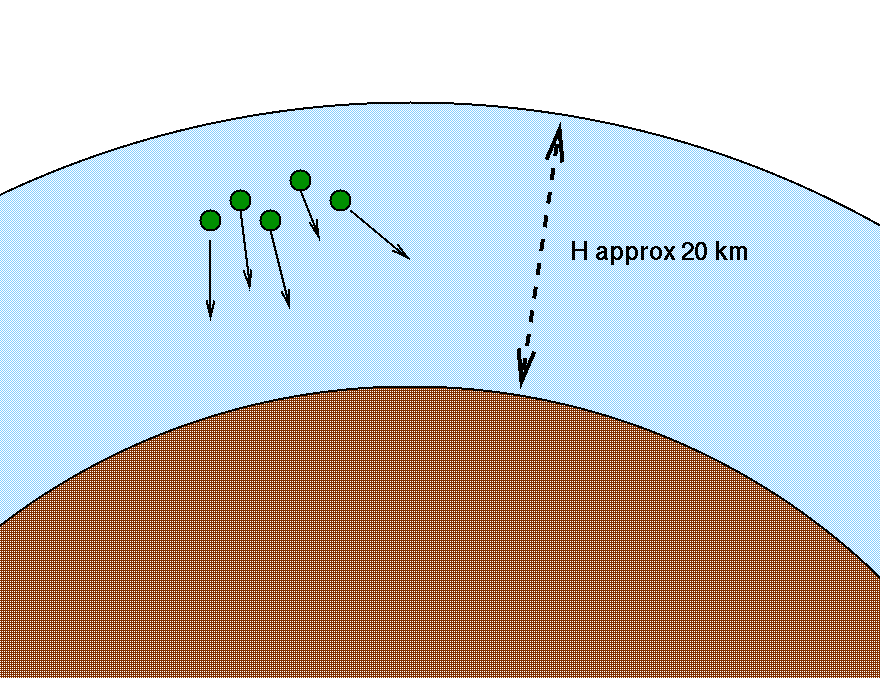
Some of the particles created in these collisions are muons. Muons are also created in reactions in the laboratory, where their lifetime has been measured:


                                    -6
    muon lifetime   t   =   2  x  10    seconds

There is no real "edge" to the Earth's atmosphere, but to a fair approximation, one can assign a height of about H = 20 km to the typical location of cosmic-ray collisions.



   Q:  If the muons created in the collision have
       speeds close to c, how far should they travel
       before decaying?


   Q:  Should any muons reach the ground?

Physicists have studied the properties of showers of particles produced by cosmic rays for over eighty years. The flux of muons (and other particles) detected is certainly larger at high altitudes, but, strangely enough, there are plenty detected right down at sea level:

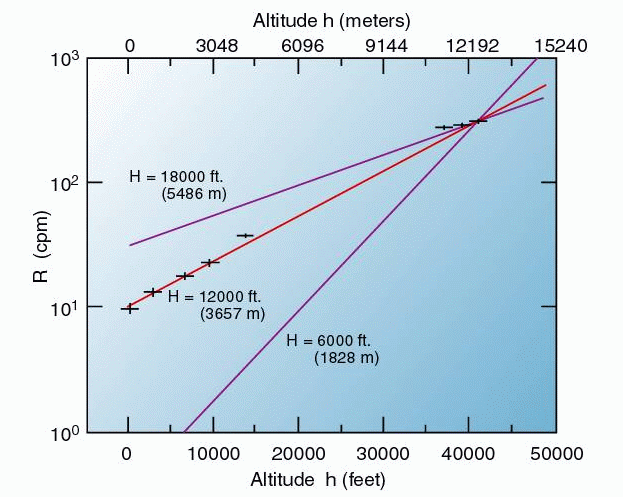
This data comes from the very nice SLAC guided tour -- see note below.

How can any muons last long enough to reach the ground? Hmmmm..... What if Einstein's idea of time dilation is correct? If the muons are moving fast enough -- relative to the Earth and people on the ground -- then their clocks will run slowly; that means that their lifetimes will be extended, perhaps long enough to reach the ground.



   Q:  How long would it take a particle travelling
       at c to go from a height H = 20 km
       down to the ground?


   Q:  By what factor of γ (gamma) must the
       muon lifetime be extended for it to reach
       the ground?


   Q:  How fast must a muon travel for it to reach
       the ground?  Express your answer as 
       a fraction of the speed of light.

When physicists measure the properties of the muons which do reach the ground, they indeed find that those particles are travelling at least as fast as the speed you've just calculated.

For more information

One of the first experiments to find evidence for time dilation in muon decay was that of Bruno Rossi and David B. Hall, published in Physical Review, vol 59, 223 (1941). It may be easier to view a local copy of the paper in PDF format.
The Stanford Linear Accelerator Center has created a very nice guided tour to a muon experiment which provides explanations and measurements.