The puzzling result of the Michelson-Morley experiment

Michelson and Morley set up their interferometer very carefully. The basic idea of the experiment is shown below, though the arrangment of the mirrors and light beams has been modified for clarity.

A light source sent beams of light (referred to as "pencils" in the paper) towards a set of mirrors. Some beams were reflected by the first mirror, and sent to mirrors which reflected them back and forth in one direction, which I'll call "vertical" (though the entire experiment was mounted on a horizontal plane, so I should really choose "East-West" or some such term): The beam eventually was sent to fall upon a screen of ground glass, inside the telescope shown in the paper's diagrams.

However, the first mirror was actually not perfectly reflective. Its surface was coated with a thin layer of silver, so that some of the light passed through it. This portion of the light was bounced by mirrors in a "horizontal" path, perpendicular to the first, before it, too, was eventually sent to the screen.

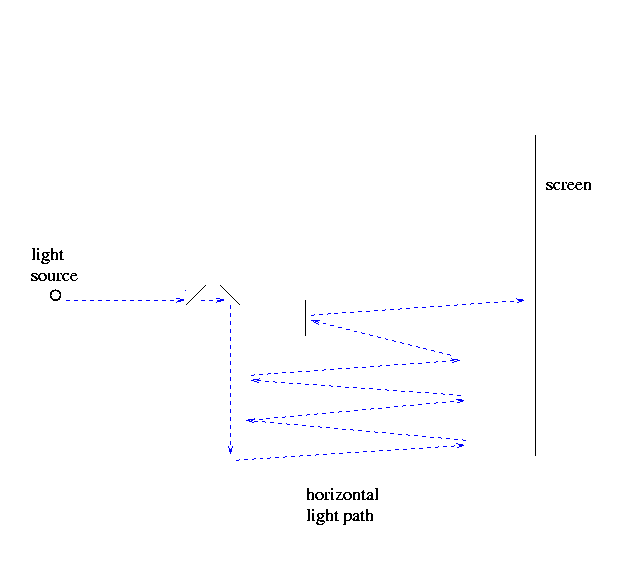
So there were two independent beams of light which travelled relatively long distances in perpendicular directions, then recombined on the screen.

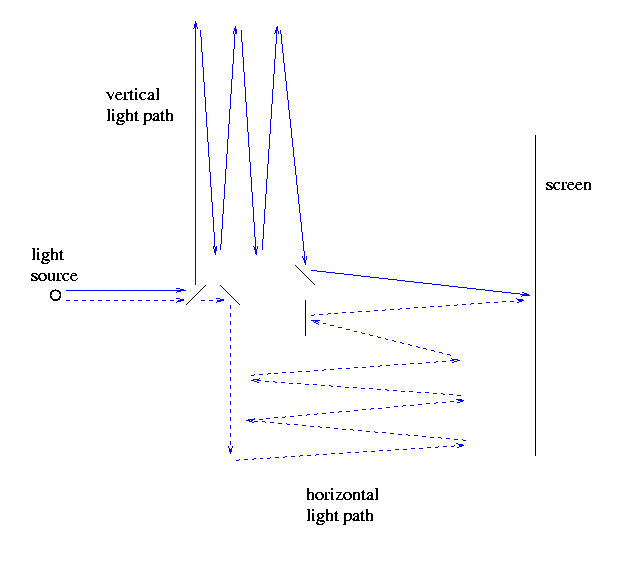
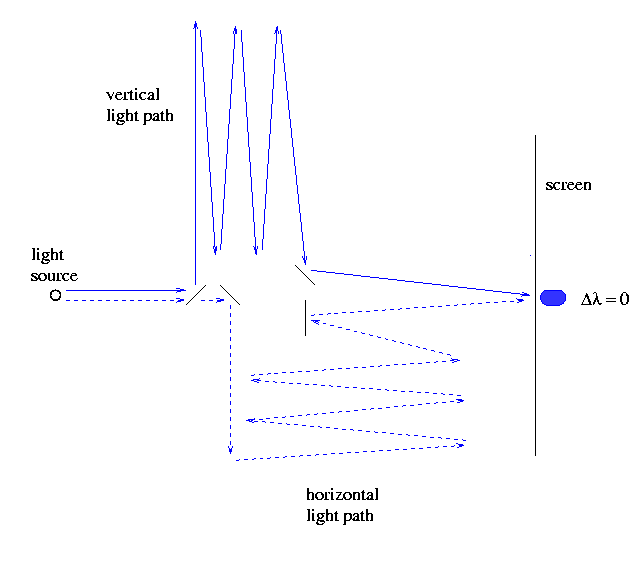
The experimenters carefully adjusted their apparatus until -- as far as they could tell -- the light paths of two beams falling on the center of the screen were equal. In other words, the difference in path lengths as zero: zero meters, zero cm, zero wavelengths of light (they used white light, so a reasonable average wavelength is about 550 nm). When two light beams meet after travelling the same difference, they interfere constructively, making a bright spot.

On the other hand, beams of light which met off-center at the screen did not travel the same distance. The difference in path length led to interference which was constructive only in a few special places: off to the side just enough to make the difference in path length exactly one wavelength:

Or further to the side, to make a difference in path length of two wavelengths:

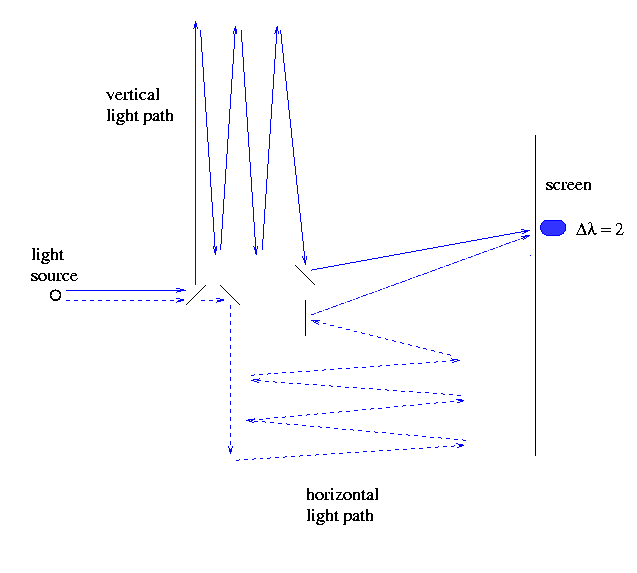
And so on across the screen. When Michelson and Morley looked at the screen (from the back side) with their telescope, they saw a series of bright spots with darkness in between.

This pattern of bright and dark areas is called "fringes" in the paper.

The fringes move ... don't they?

Now, what would happen if things changed so that light took a bit longer to pass through one leg of the interferometer? Suppose that initially, the apparatus was arranged so that both paths were oriented 45 degrees away from the motion of the Earth through the ether:

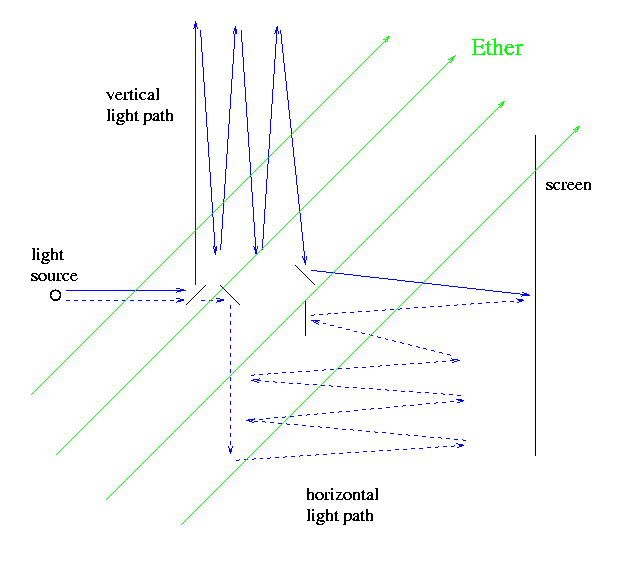
But if one rotates the experiment -- as Michelson and Morley did -- then at some point, one of the legs will be parallel to the direction of the ether drift, and the other leg will be perpendicular.

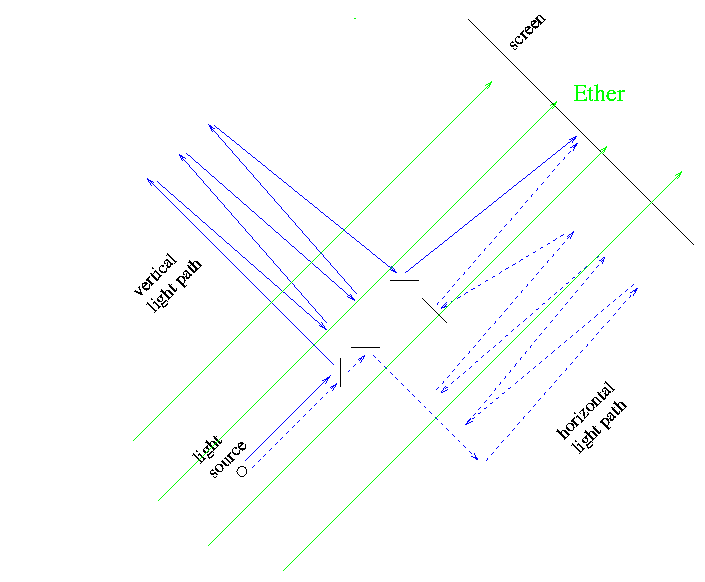
If the theory that light propagates through the ether is correct, then at this point, the light beam travelling "up-and-back" along the ether drift (the horizontal path) will take longer to reach the screen than the light travelling "across" the ether drift (the vertical path). That means that when the two light beams meet at the middle of the screen, they won't be in phase any longer:

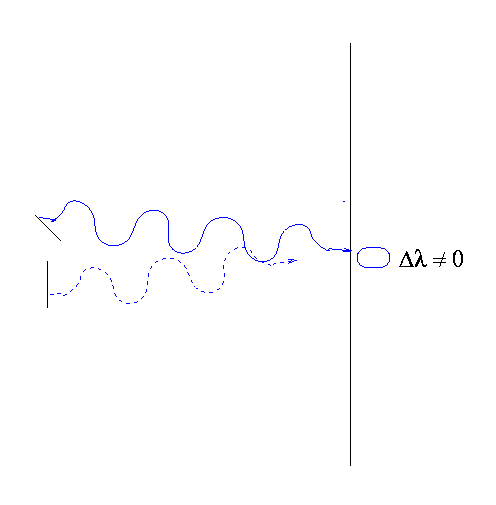
However, a little bit lower on the screen, closer to the mirror reflecting the delayed light beam, the two waves will meet in phase.

Someone looking at the screen would see a small shift in the position of the bright spots; the shift depends on the difference in time (or, equivalently, path length) it takes for the two beams to travel through the two legs of the interferometer.

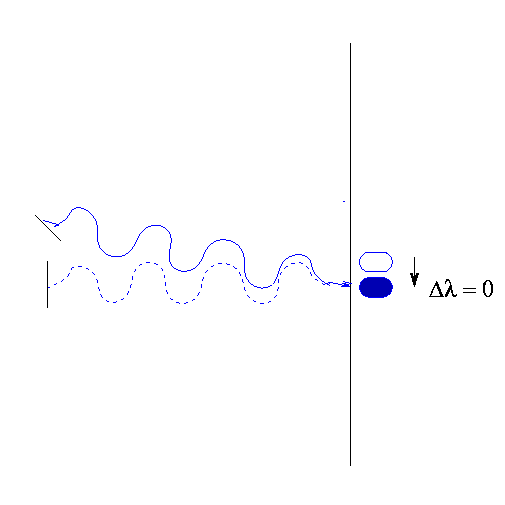
Michelson and Morley expected to see a shift of this sort as they rotated their experiment on its stone table. They were able to measure shifts in the position of the fringes which were only a small fraction of the space between the bright spots. Based on the motion of the Earth around the Sun, they predicted that the shift in position ought to be roughly 40% of the distance between the fringes (which they denote, confusingly, as lambda). Yet what they saw was:

In short,

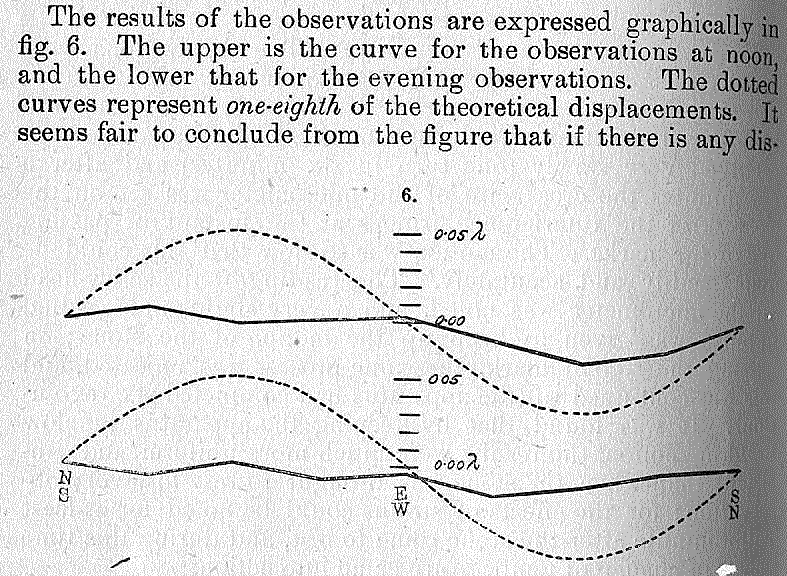
NO SHIFT

Something had to be wrong -- in the experiment, or the theory. Michelson and Morley were confident that the experiment was not at fault. But, then, how to explain the lack of any shift with the rotation of the apparatus?