The Lorentz Transformations


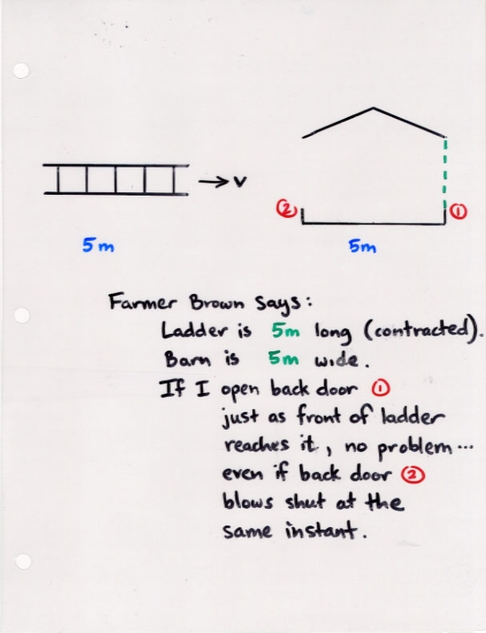
   So, what happens?

How to record properly the time and location of events

One problem here is that we need to keep track of two sets of quantities (position, time, length, etc.):

one in Fred's frame of reference
one in Farmer Brown's frame of reference

We will use a set of equations called the Lorentz transformations to convert quantities in one frame to those in another...

But another, more fundamental, problem is deciding exactly what constitutes a valid measurement. In the world of Einstein, one must be VERY careful in measuring exactly where and when an event occurs.

For example, consider a ball rolling towards a flag. When, exactly, does the ball reach the flag?

If the observer stands far from the flag, then there will be a small delay between the time that the ball actually strikes the flag, and the time he sees the ball strike the flag -- just because light will take a short time to travel from the flag to his eyes. So, rule number 1:

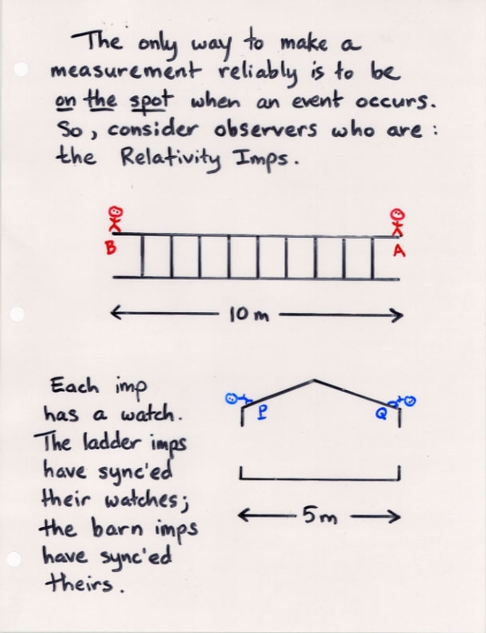
Observers must stand at the same place as the event they are measuring.

Now, suppose that we are interested in two events which occur at different locations; for example, the interval between the time at which the ball reaches the first flag and the time at which it reaches the second flag:

A single observer cannot be at both locations at once ... and, as you might well suspect, complications will set in if he tries to measure the first event, then run at high speed to the location of the second event before it happens. No, a single observer just won't do. What we need to measure several events is a whole army of observers.

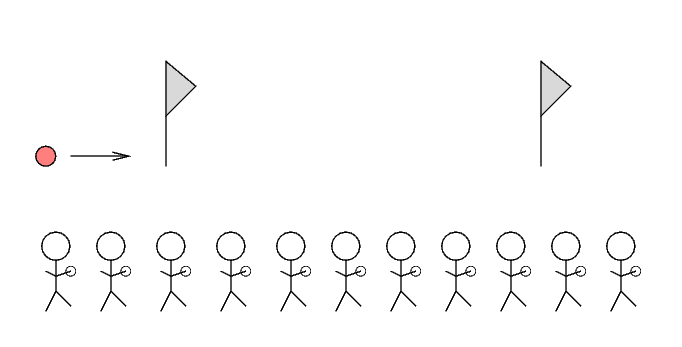
This army of observers must satisfy two conditions:

they must all be in the same inertial frame
they must synchronize their watches before they start taking measurements


  Q: How can they synchronize their watches?

Now, once they are ready, they simply watch and wait. When an event occurs, the observer who happens to be at that location notes the time on his watch.

This insistence on niggling little details of the process of measuring times and locations may seem annoying, but it's necessary to use the Lorentz transformations properly.

Back to the barn and ladder ...

It turns out that there are special rules for converting the measurements made by a stationary observer to those made by a moving observer.

Viewgraph 1

Note that the equation for position in the moving coordinate system has both position and time from the stationary coordinate system. That's not unusual: in everyday life we often use time to describe space.

It's about two hours to Niagara Falls from Rochester.

The unusual feature of these equations appears in the last one: the equation for time in the moving coordinate system includes both time and space from the stationary system. We don't encounter that very often in our ordinary lives. In other words, you don't often hear someone say,

Boy, that movie must have lasted for thirty yards!

It is this mixing of the time and space coordinates that gives rise to the term spacetime, which you may have heard in discussions of relativity.

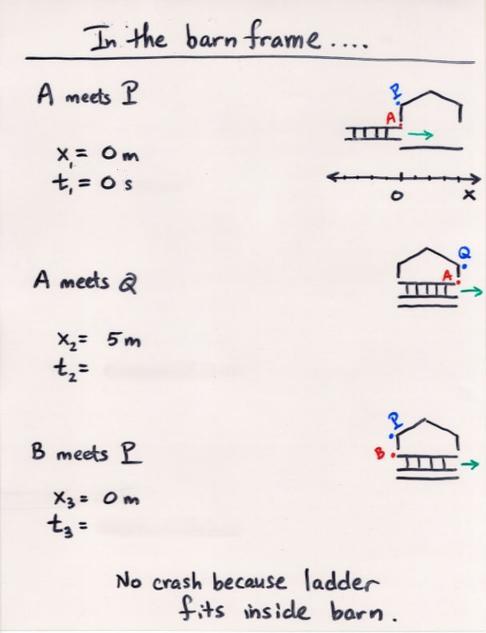
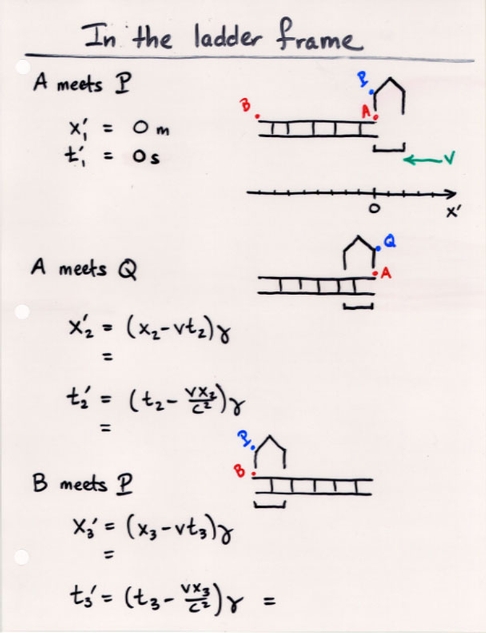
Now, back to the barn-and-ladder problem: recall that

Fred says his ladder is 10 m long
Farmer Brown says his barn is 5 m wide
Fred runs at v = 0.866 c towards the barn

For our convenience, let's stipulate that the clocks carried by imps P and A both happen to read zero when they meet. It won't affect any of the conclusions, but it will simplify these calculations.