The Franck-Hertz experiment supports Bohr's model

In 1914, James Franck and Gustav Hertz published the results of an experiment which provided strong evidence that Bohr's model of atoms with quantized energy levels was correct. But, in the haphazard manner of real research, the authors weren't trying to test Bohr's model; in fact, they weren't even aware of Bohr's theory!. As Franck admitted later

"It might interest you to know that when we made the experiments that we did not know Bohr's theory. We had neither read nor heard about it. We had not read it because we were negligent to read the literature well enough -- and you know how that happens. On the other hand, one would think that other people would have told us about it. For instance, we had a colloquium at that time in Berlin at which all the important papers were discussed. Nobody discussed Bohr's theory. Why not? The reasons is that fifty years ago, one was so convinced that nobody would, with the state of knowledge we had at that time, understand spectral line emission, so that if somebody published a paper about it, one assumed, "Probably it is not right." So we did not know it. But we made that experiment (and got the result that confirmed Bohr's theory) because we hoped that if we found out where the borderline between elastic and inelastic impact lies ... only one line might appear. But we did not know whether that would be so, and we did not know whether at all an emission of an atom is of such a type that one line alone can be emitted and all the energy can be used for that purpose. The experiment gave it to us, and we were surprised about it. But we were not surprised after we read Bohr's paper later, after our publication."

-- Excerpt from one of three recordings of J. Franck, made in connection with a film on the Franck-Hertz experiment at Educational Services, Inc., Watertown, Massachusetts, in January, 1961. As transcribed in "On the recent past of physics", by Gerald Holton, American Journal of Physics, vol. 29, p. 805 (1961).

A nice accident, to win a Nobel Prize (1925) for an experiment that you didn't really understand at the time.

In addition, Franck and Hertz interpreted their experimental results incorrectly in the paper below: they believed that the collisions between electrons and mercury atoms were ionizing the mercury atoms; but actually the collisions were exciting the mercury atoms from their ground n=1 state to the first excited n=2 state.

Fortunately, other scientists quickly realized how this experiment did confirm Bohr's hypothesis that atoms make only certain transitions between discrete energy states.

So, the idea is that when an electron runs into a mercury atom, there are two outcomes. If the incoming electron has a kinetic energy which is less than the difference delta E between mercury's n=1 and n=2 energy levels, then it simply bounces off elastically, keeping all its original kinetic energy:

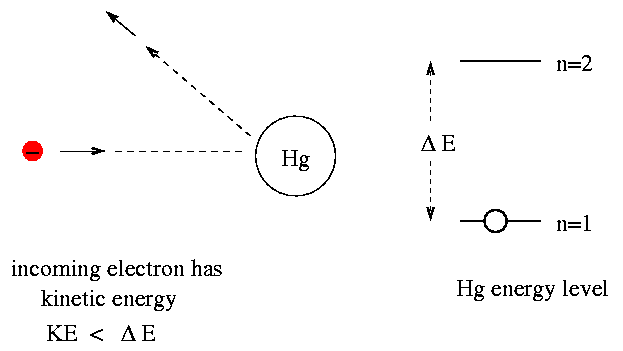
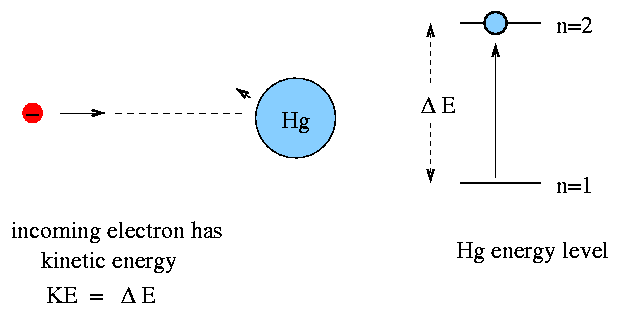
But if the electron has kinetic energy equal to (or a bit greater than) delta E, then it transfers most of its kinetic energy to the mercury atom, boosting the atom to the n=2 state. That leaves the electron with very little kinetic energy.

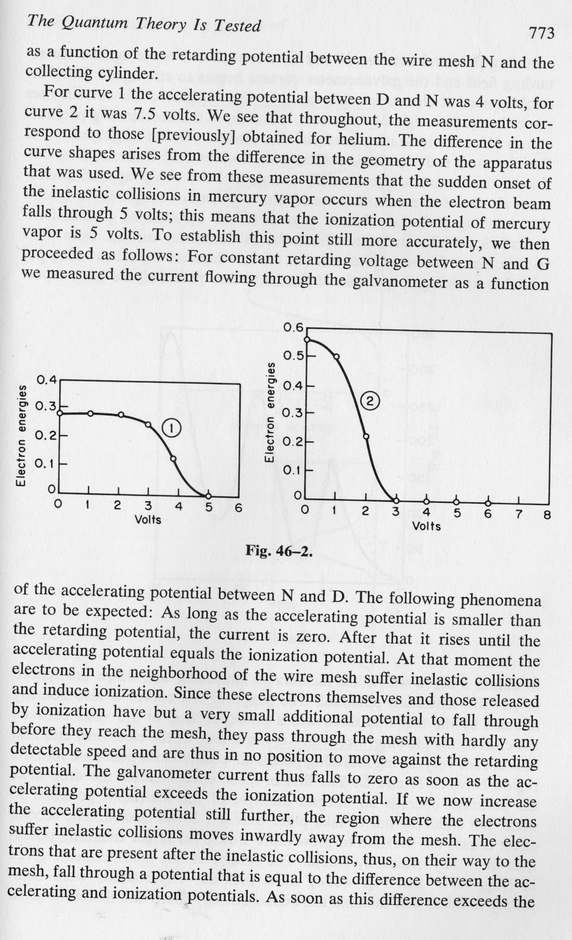
Let's look at what happens inside their apparatus. There's a hot platinum wire at the center (D), then a wire mesh with a positive voltage (N), all surrounded by a foil with a small negative voltage (G). The hot wire spits out electrons ...

The end result a current flowing from the wire to the outer foil.

Now, if we fill the tube with mercury gas in atomic form, the electrons can bounce off the atoms as they fly towards the mesh ...

Once again, a current flows through the apparatus.

However, if we increase the voltage on the wire mesh to a critical point, we give the electrons enough kinetic energy that they can excite mercury atoms from the ground state (n=1) to the first excited state (n=2) when they collide.

So, in this case, we find very little current flowing.

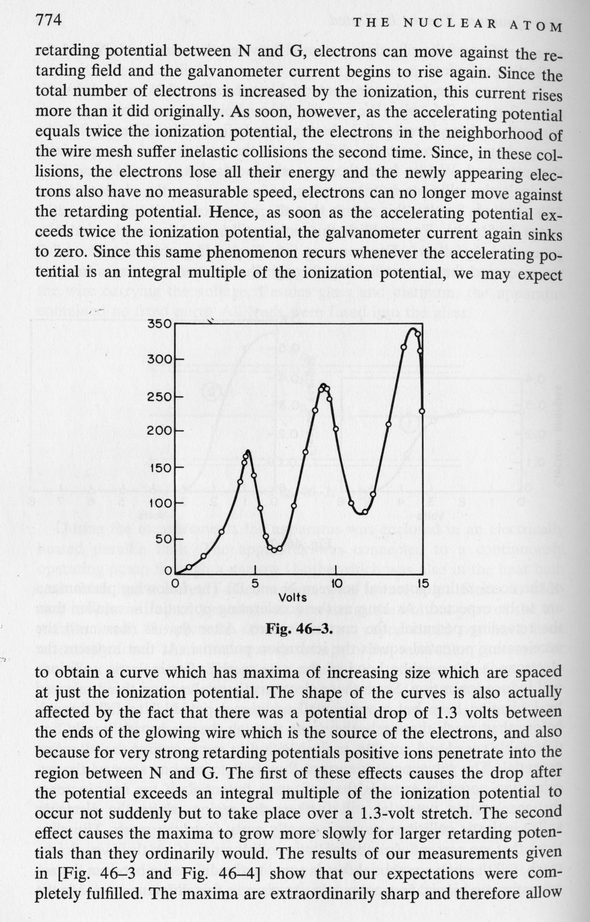
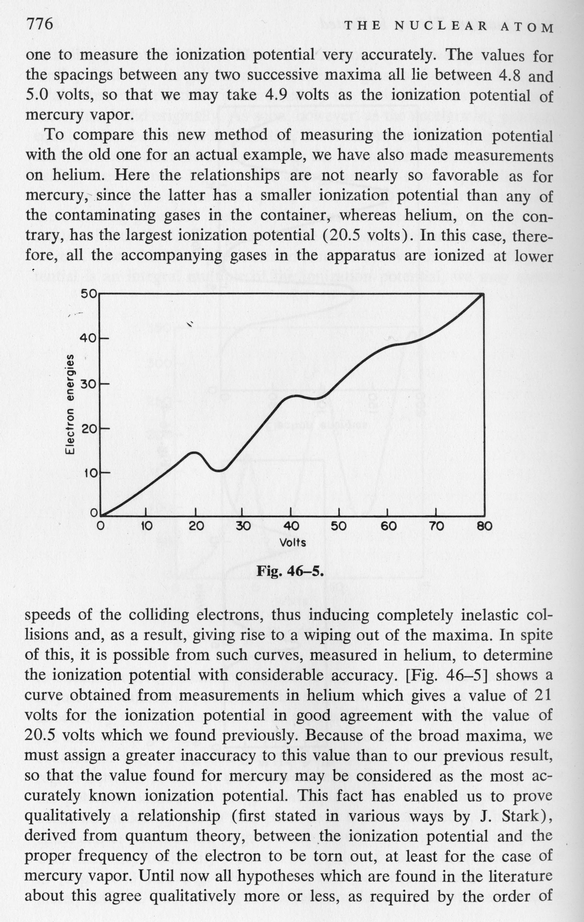
Note the multiple peaks in current, separated by equal voltages. These correspond to situations in which electrons lose most of the kinetic energy in a single collision, or in two collisions, or in three collisions, and so forth. Each collision costs the same amount of energy, because almost all the mercury atoms are in the ground state: the mercury atoms jump back down from the excited n=2 state to the n=1 state in a short time.

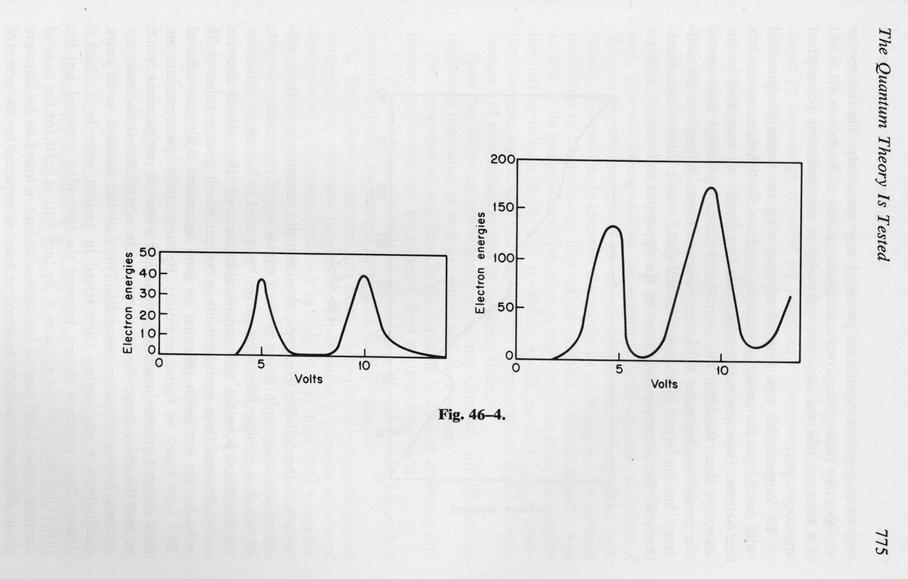
What is the energy which electrons lose in each of these collisions?

express as electron-volts
express as Joules

What is the difference in energy levels between the n=2 and n=1 states of mercury?

express as electron-volts
express as Joules

After it has been excited into the n=2 state by a collision, the mercury atom very quickly emits a photon and drops back to the n=1 state.


Q: What is the wavelength of that photon?

Q: What is the color of that photon?

Remember, the last point, number 4, is not quite correct. The mercury atoms are NOT being ionized by their collisions with electrons; they are simply being bumped upwards into an excited state.


How does this experiment support Bohr's model?