Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
In 1927, a paper by Davisson and Germer appeared in volume 30 of The Physical Review:
The authors described a set of experiments in which they shot electrons at a crystal of nickel and measured the intensity of the scattered electron beam at different angles. The results confirmed De Broglie's hypothesis that electrons (like all matter) ought to exhibit wave-like properties.
But how did this all start? Did Davisson and Germer set out to test De Broglie's theory? No! It all began with an accident in their lab, six years earlier:
Note their frank statement that they didn't see what they expected to see:
We must admit that the results obtained in these experiments have proved to be quite at variance with our expectations.
They thought that electrons would be have like little balls when shot into a crystal lattice. If they fired electrons in just the right direction, along one of the lattice rows, they expected the electrons to pass straight through:
But if they shot the electrons into the crystal at any other direction, they expected the electrons to run into an atom and bounce back:
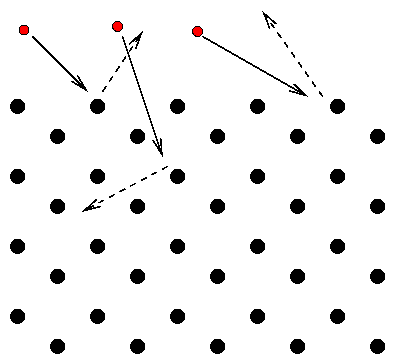
They did see strong beams of scattered electrons, but not where they expected to see them:
Speed? What should the speed of the electrons have do with them bouncing back?
This is a puzzle. Let's look closely at their actual setup.
Their apparatus was a small evacuated glass vessel inside which were an electron gun (G), a target crystal of nickel (T), and a collector (C) -- a metal plate attached to a circuit.
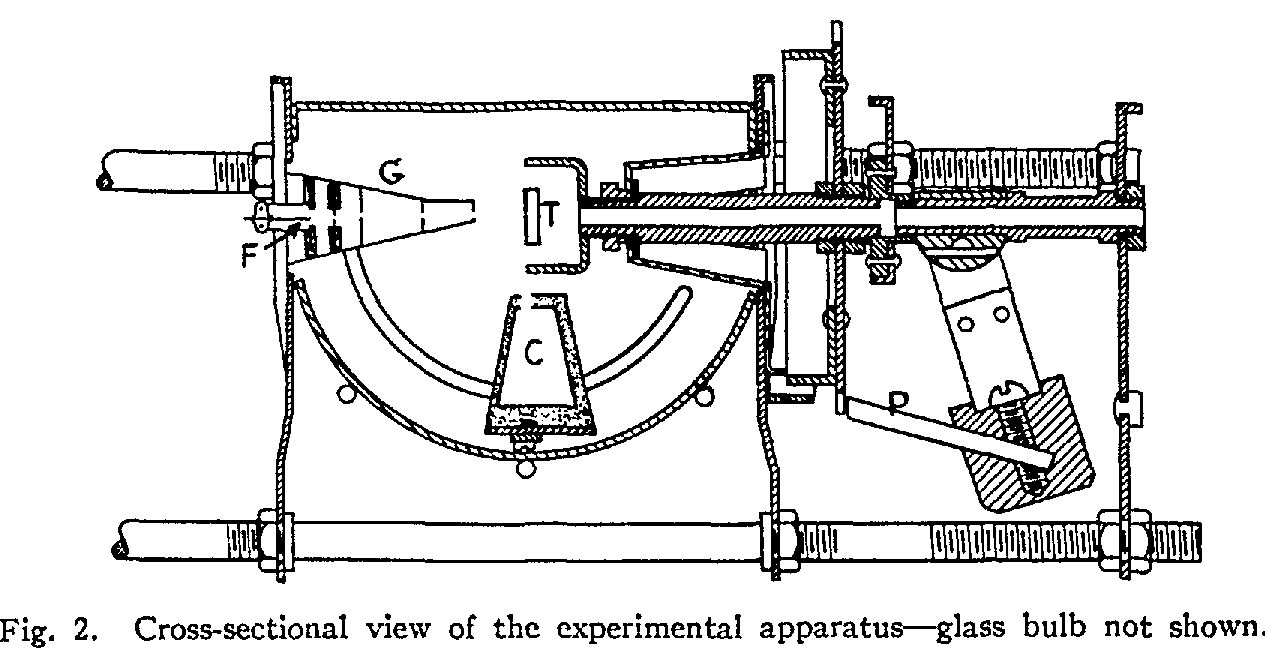
Electrons were accelerated across a voltage V, then shot at the target. The collector was moved to various angles relative to the incoming beam. Electrons which scattered off the crystal in the right direction would collect on the metal plate, completing a circuit. By measuring the current, Davisson and Germer could determine the intensity of the scattered electron beam at any particular angle.
As a general rule, the intensity of scattered electrons didn't vary much. However, the experimenters noticed that certain combinations of electron-gun voltages V and angles theta yielded an intensity much higher than average.
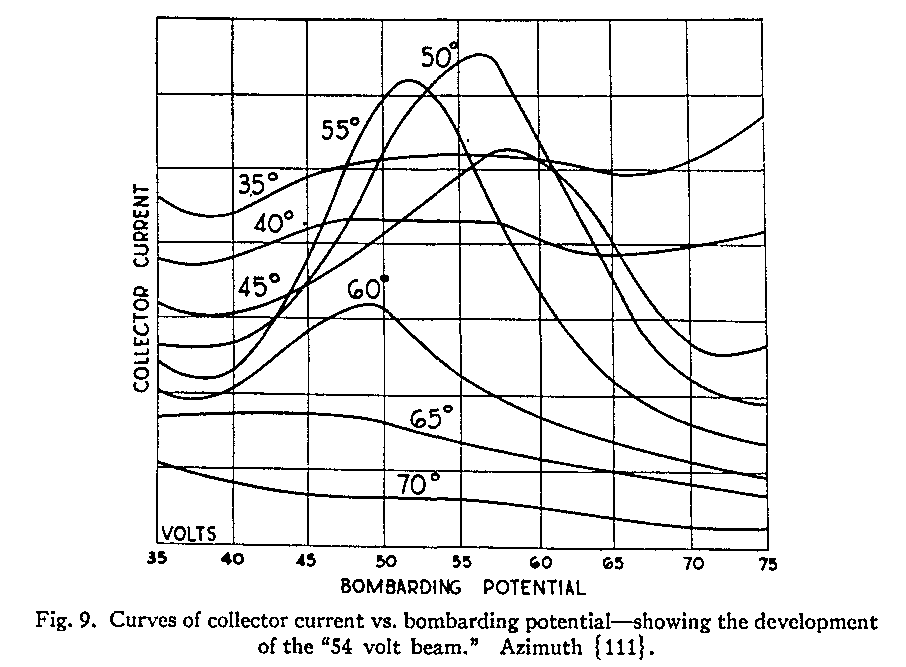
The were two combinations in particular which gave very strong scattered signals:
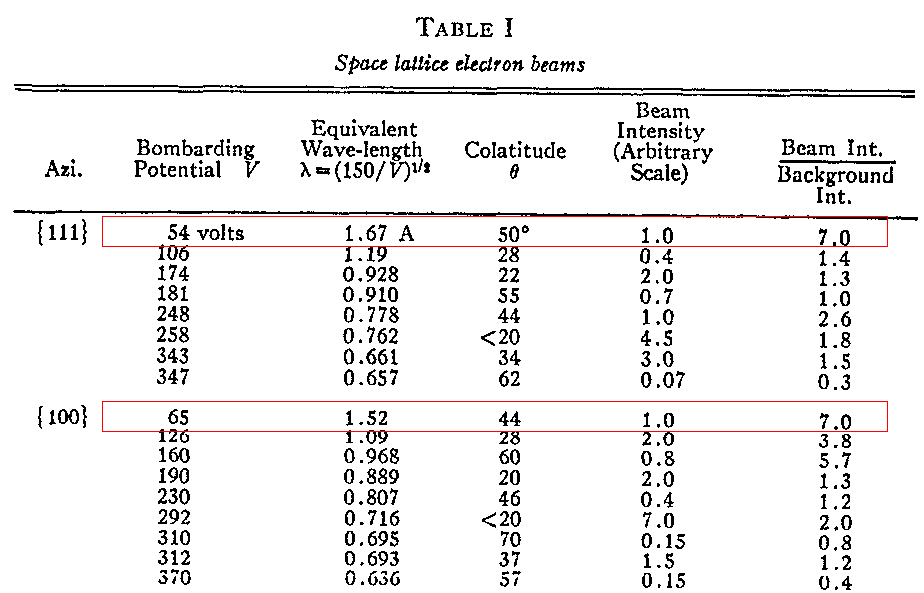
Davisson and Germer interpreted these signals as constructive interference of electron waves scattered from the crystal. Assuming that these very strong signals correspond to the first bright spot of a diffraction pattern, what must the spacing of the grooves be?
Of course, the nickel wasn't really a simple diffraction grating. Davisson and Germer knew that that atoms in the crystal were arranged in a regular lattice, like this:
Click on the chart above to see a simplified version, showing only the atoms in the top-most layer of the crystal. If the "grooves" are consecutive rows of nickel atoms in the crystal (separated by distance d), and if De Broglie's hypothesis is correct, what is the distance s between nickel atoms in the crystal?
Hmmmm.... is that the actual spacing between atoms in a nickel crystal?
Apparently they do. In most of our interactions with electrons, they behave like tiny little hard spheres with an electric charge ... but, in this experiment, they show the characteristics of waves.
Davisson wrote about the apparent confusion (Franklin Institute Journal, vol 205, p. 597 (1928); reproduced in The World of the Atom, ed. Boorse and Motz)
It is rather as if one were to see a rabbit climbing a tree, and were to say, "Well, that is rather a strange thing for a rabbit to be doing, but after all there is really nothing to get excited about. Cats climb trees -- so that, if the rabbit were only a cat, we would understand its behavior perfectly."
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.