Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Light can apparently behave like a particle, or like a wave? But under certain circumstances, it must somehow behave like both at once.
One of the first experiments of this sort was described by Hellmuth, Walther, Zajunc and Schleich, in Physical Review A, vol 35, p. 2532 (1987). The scanned results and conclusion from that paper are shown below. A slightly earlier paper by Alley et al., in Proceedings of the International Symposium on Foundations of Quantum Mechanics, (Tokyo, 1986), describes a very similar experiment, but is much harder to find.
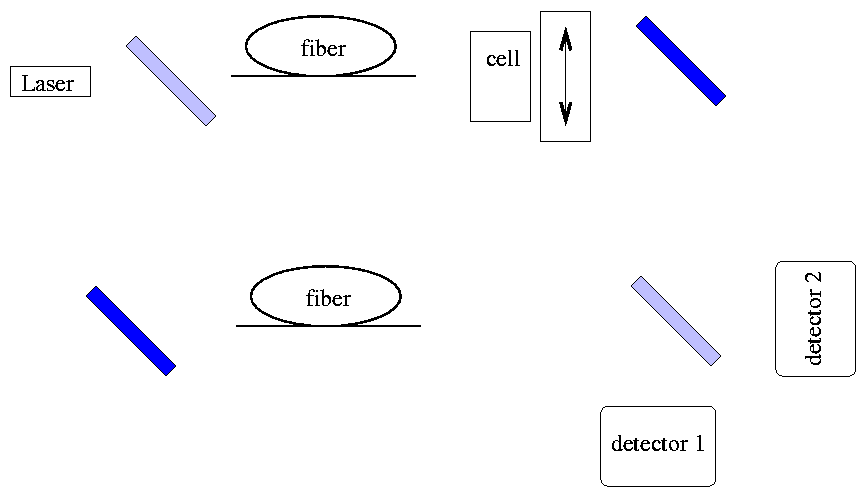
The basic idea of the experiment is to set up an interferometer with two legs. Each leg has a loop of optical fiber about 5 meters long.
Q: How long will it take a ray of light to pass through the fiber?
One of the legs also has a "Pockells cell", which acts like a piece of polarizer, followed by a second polarizer. The Pockells cell can be switched from one polarization state to another very quickly -- in about 4 ns.
The blue rectangles in the diagram above represent mirrors. The solid blue ones are ordinary mirrors which reflect 100% of the light striking them; the light blue ones are "half-silvered" mirrors, also called "beam splitters", which reflect 50% of the light and transmit the other 50%.
Now, let's consider what happens if light is composed of discrete pieces: photons. We have a couple of photodetectors at the end of the photometer -- what will they read when we send a pulse of light out of the laser?
Suppose we set the Pockells cell so that it only allows horizontally polarized light to pass through it. This effectively "closes" the upper arm of the interferometer, because any photon passing through the cell will immediately be blocked by the fixed polarizer behind it.
Click on the picture below, or any picture with a box around it, to view an animation.
Since 50% of the photons from the laser will pass through the first beam splitter, we expect that 50% of the time, both the detectors will read 0.
On the other hand, 50% of the time, the photon will bounce off the first beam splitter and head towards the lower leg. What will happen then? Well, half of the time (25% overall), the photon will pass through the second beam splitter and into Detector 2.
The other half of the time (25% overall), the photon will bounce off the second beam splitter and into Detector 1.
So, putting it all together, if light behaves like a photon, and we close the upper arm, we expect to see
probability Detector 1 Detector 2
------------------------------------------------------------------------
blocked in upper arm 50% 0 0
lower arm, through 25% 0 1
lower arm, bounce 25% 1 0
------------------------------------------------------------------------
Q: If we sent 200 photons into the device, what would we
expect to read from the detectors?
Now, suppose light acts like a wave instead. If we open the upper arm by setting the Pockels cell parallel to the fixed polarizer, light will go through both of the arms and interfere when it reaches the detectors:
The experimenters carefully arranged their apparatus so that the path along one arm was half a wavelength longer than along the other arm. If constructive interference occurred at one detector, then destructive interference would occur at the other. The sum of the detected intensity would add up to 1.0, but it would be divided between the two in some way.
When Hellmuth and his colleagues ran the experiment, they discovered that small temperature variations in the fibers caused the exact path lengths to vary slowly, on timescales of a minute or two. That meant that the form of the interference drifted during their observations: Detector 1 would first have constructive interference, then it would gradually change to destructive, then back again. Their measurements looked something like this:
time (sec) Detector 1 Detector 2
------------------------------------------------------------------------
0 0.90 0.10
30 0.60 0.40
60 0.30 0.70
90 0.05 0.95
120 0.15 0.85
------------------------------------------------------------------------
and so on.
Q: If we sent 200 photons into the device, all during a 30-second period,
what would we expect to read from the two detectors?
Q: Suppose we make many sets of measurements, over several minutes.
Should these readings change with time?
Now, here's where the delayed choice comes into play. Suppose that we start out with the Pockells cell set so that the upper arm is closed, and let a single photon into the device.
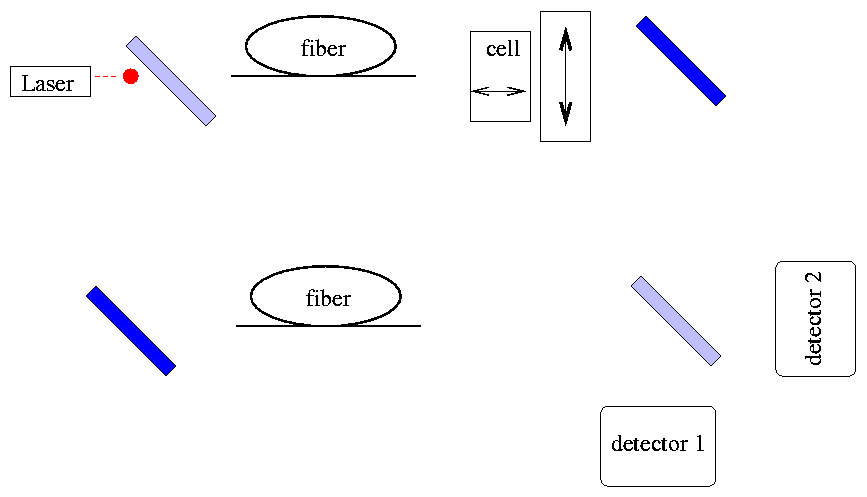
If the photon is "looking ahead", it will realize that in this situation, it can never reach the detectors along both legs; it can either go through the first beam splitter and be aborbed by the fixed polarizer, or bounce off the beam splitter and run through the lower leg. Suppose it takes the second route. We wait 15 ns, until the light has moved past the first beam splitter and into the optical fiber ...
and NOW we switch the Pockels cell so that it opens the upper leg:
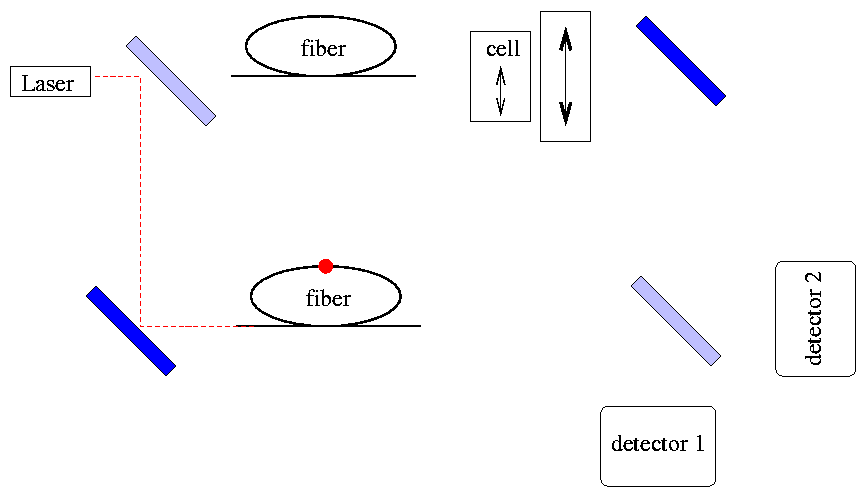
What is the poor photon to do? It is "stuck" in the lower leg of the interferometer, and must continue so that it ends up in either detector -- but not both. There can be no interference in this case.
Q: If we sent 200 photons into the device, making the "delayed choice"
each time, what would we expect to read from the two detectors?
Q: Suppose we make many sets of measurements, over several minutes.
Should these readings change with time?
There's clearly a difference between the measurements we ought to make if light is only a photon, or if light can be both a photon and wave at the same time. The scientists who ran the experiment arranged it to do the following:
Let's look at their results:
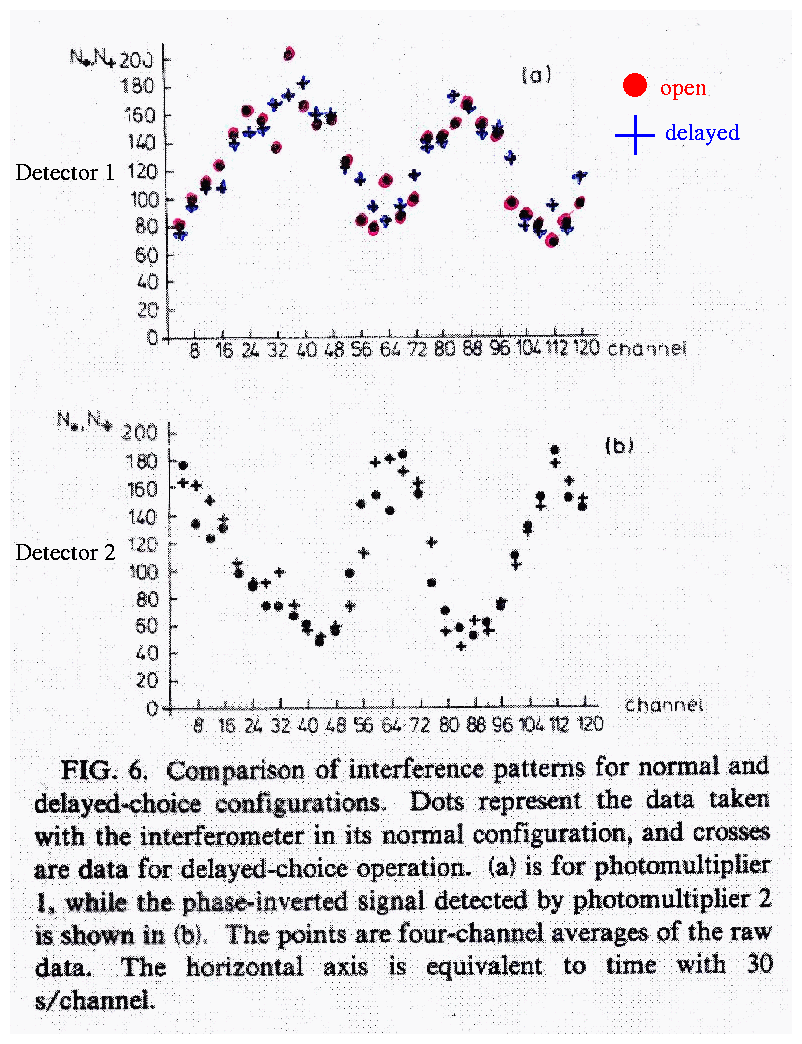
You can read a short essay on the puzzle of this duality by John Archibald Wheeler.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.