 Viewgraph 1
Viewgraph 1 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
q(t) = q0 * exp(-t/RC)
I(t) = I0 * exp(-t/RC)
q(t) = q0 * [ 1 - exp(-t/RC) ]
= CV * [ 1 - exp(-t/RC) ]
where V is the voltage of the battery charging the capacitor
I(t) = I0 * exp(-t/RC)
= (V/R) * exp(-t/RC)
 Viewgraph 1
Viewgraph 1
 Viewgraph 2
Viewgraph 2
 Viewgraph 3
Viewgraph 3
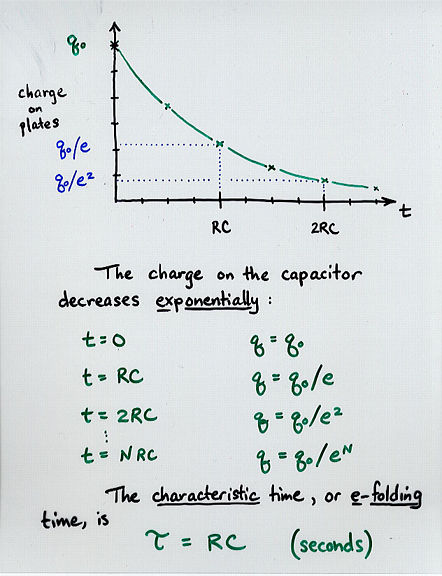 Viewgraph 4
Viewgraph 4
 Viewgraph 5
Viewgraph 5
 Viewgraph 6
Viewgraph 6
 Viewgraph 7
Viewgraph 7
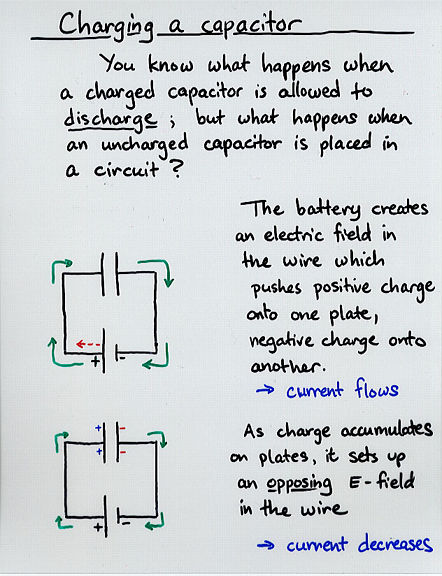 Viewgraph 8
Viewgraph 8
 Viewgraph 9
Viewgraph 9
 Viewgraph 10
Viewgraph 10
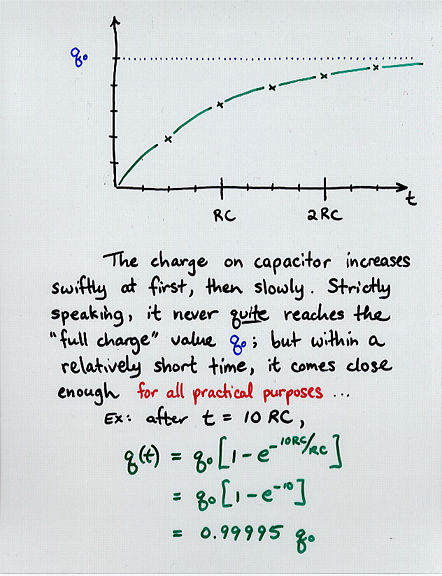 Viewgraph 11
Viewgraph 11
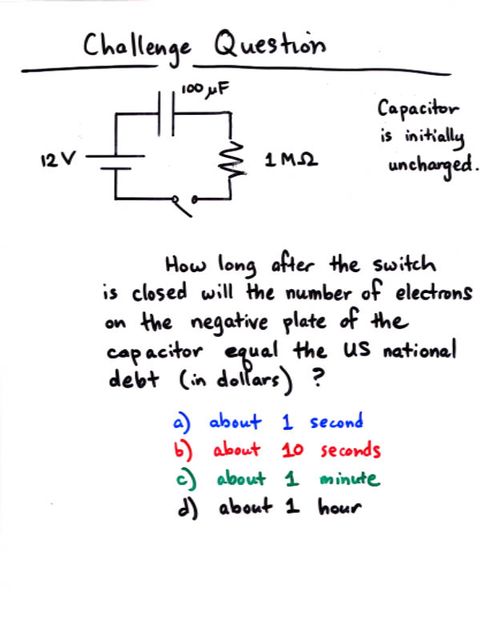 Viewgraph 12
Viewgraph 12
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.