Multipole Expansions

• Scientists of all kinds often try to approximate a complicated phenomenon by adding together a few simple pieces.
  • Fourier series
  • Bessel functions
  • Primary Component Analysis
  • Spherical harmonics
  Another of these methods, multipole expansion, is especially suitable for electric fields of common molecules.
• A monopole is a point charge. Its electric field falls off as 1/r^2.
• A dipole is a pair of opposite charges, separated by a small distance. Its electric field falls off as 1/r^3 at large distances
• A quadrupole is a set of 4 charges, 2 positive and 2 negative, arranged in a symmetric cross. Its electric field falls off as 1/r^4 at large distances

Viewgraph 1

Viewgraph 2

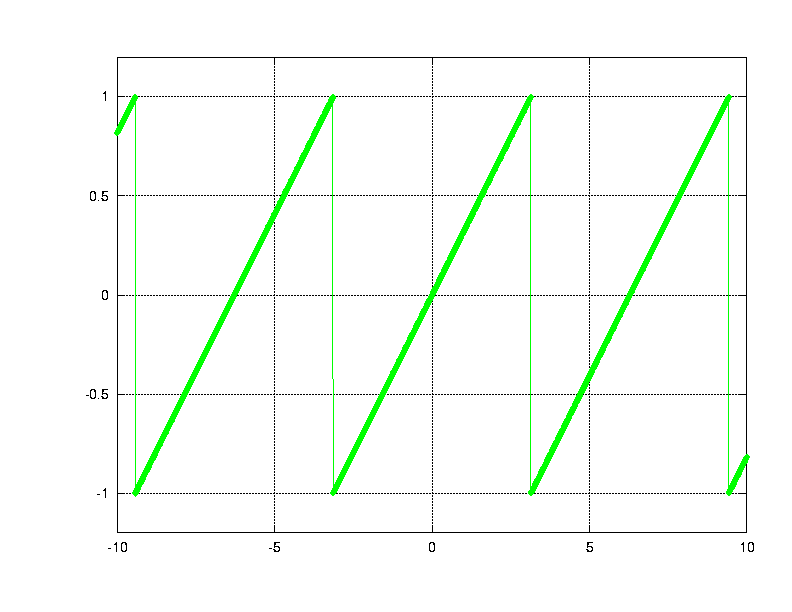
An example of using the Fourier series to approximate a sawtooth wave.

A complicated function -- the sawtooth wave -- which we want to approximate with simple sinusoidal functions.

The first Fourier term: a single sinusoid.

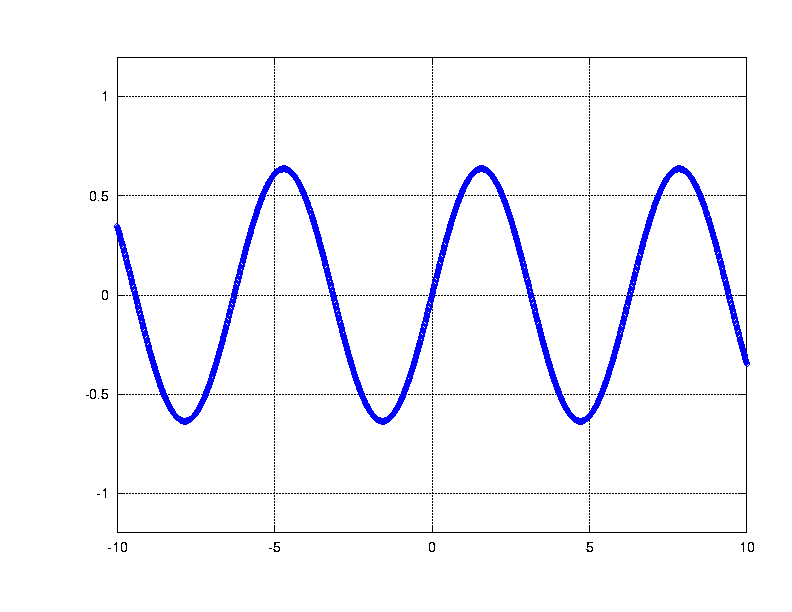
How well does it fit the complicated function? Not very.

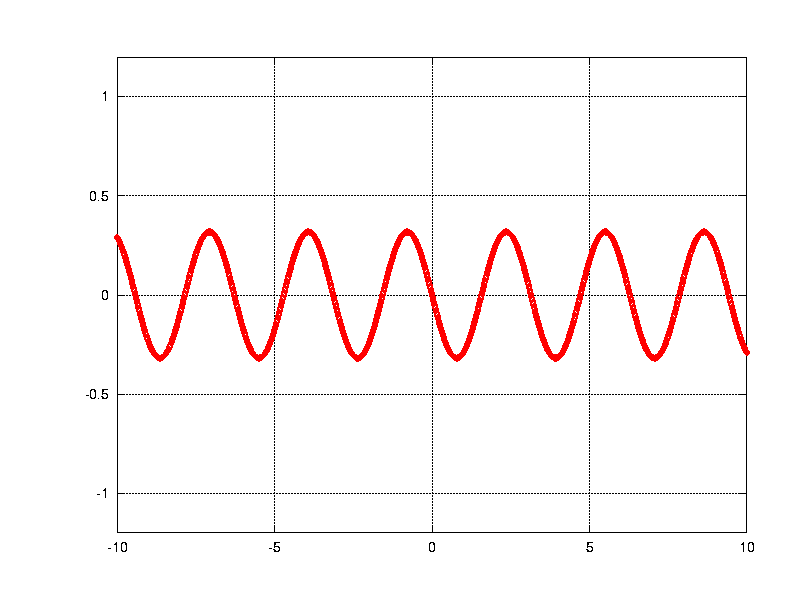
The second Fourier term.

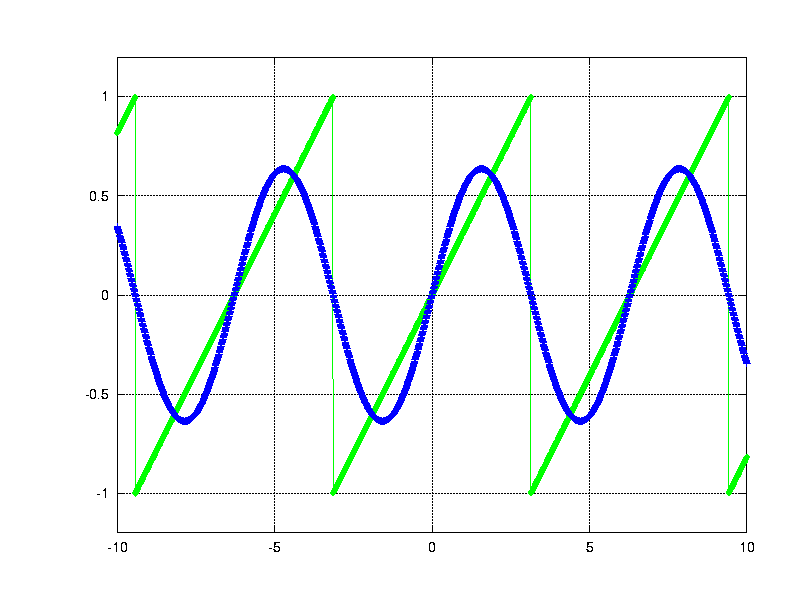
Add together the first and second Fourier sinusoids -- how well do they fit the sawtooth?

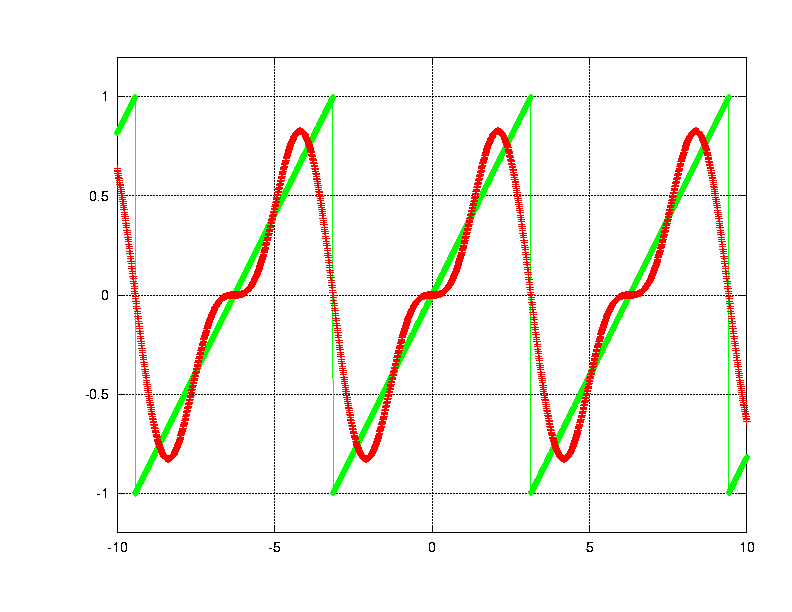
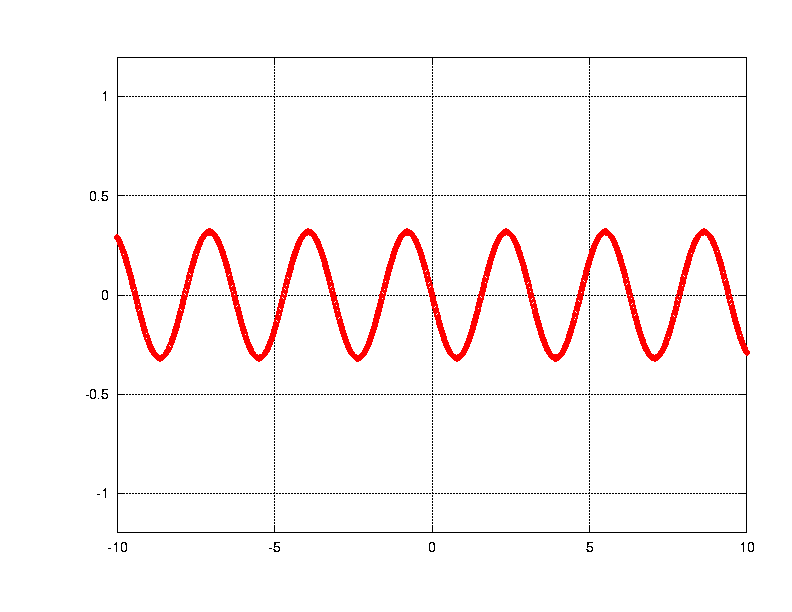
The third Fourier term.

Add together the first, second and third Fourier sinusoids -- how well do they fit the sawtooth? Pretty well.

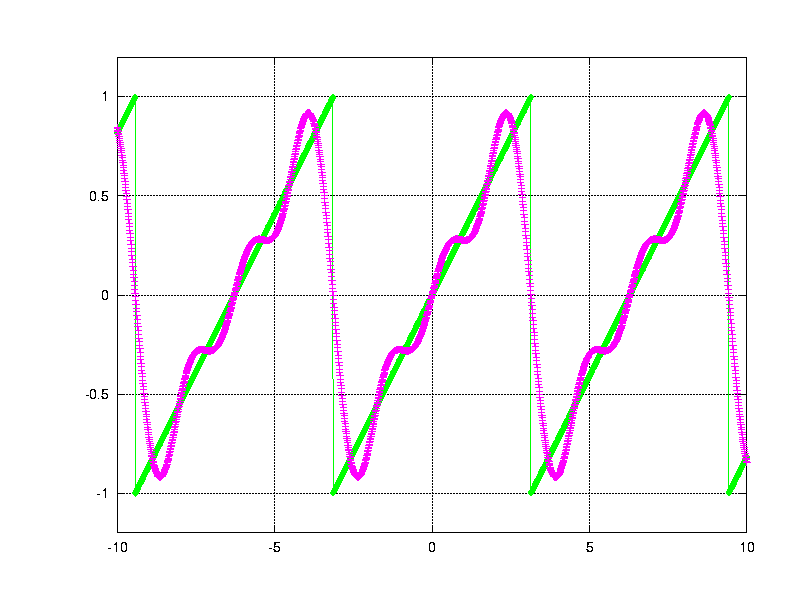
Viewgraph 3

Viewgraph 4

Viewgraph 5

Viewgraph 6

Viewgraph 7

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.