Magnetic Fields and Currents

This lecture is based on HRW, Sections 29.7-29.9. It covers the effect of magnetic fields on currents running through wires.

A magnetic field exerts on a force on a wire (or other conductor) when a current passes through it.
The general formula for determining the size and direction of the magnetic force on a current-carrying wire involves a complicated integral
There are several cases in which the solution is relatively easy: (note that each one involves a cross product of two vectors)
- Straight wire in uniform magnetic field:
```
             F = I (L x B)
   
```
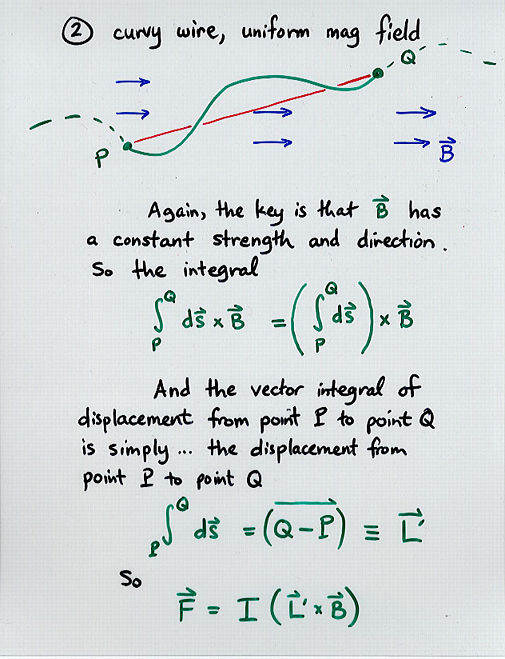
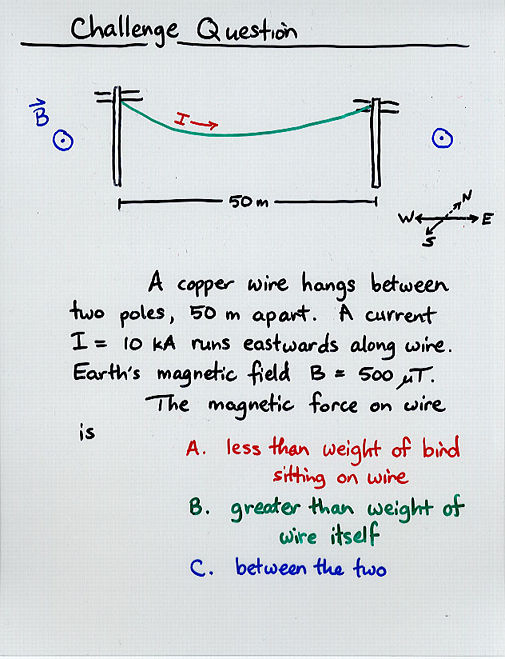
- Curved wire in uniform magnetic field:
```
             F = I (L' x B)
   
```
  where L' is a straight vector from the starting point of the wire to its end point
- Closed circuit loop in a magnetic field:
```
             F = 0
    
```
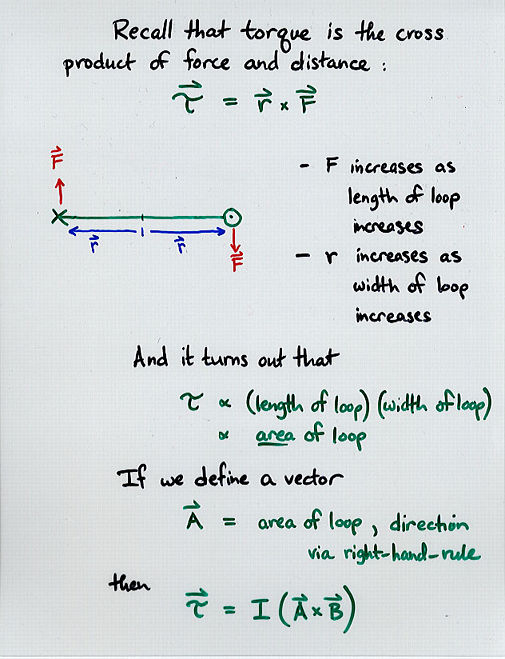
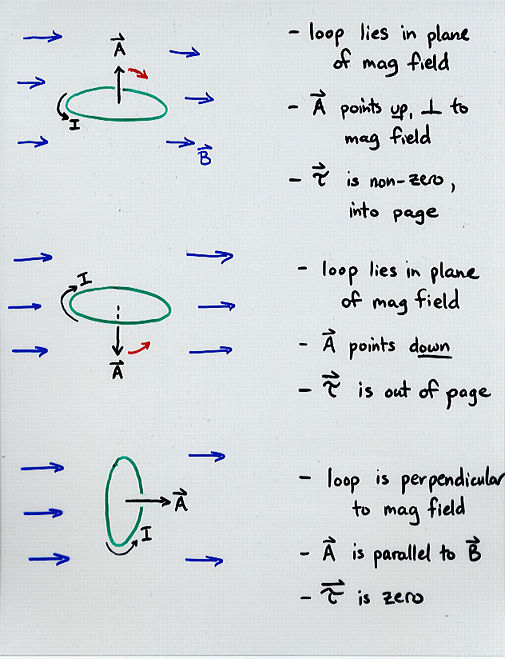
Although the force on a closed loop of current in a uniform magnetic field is zero, the torque is not.
If one defines a special "area vector" A, the magnitude of which is the area of the closed loop, and the direction of which is perpendicular to the plane of the loop (as given by right-hand rule), then the torque on the loop is
```
             tau = I (A x B)
```
The torque acts to make the "area vector" parallel to the direction of the magnetic field
The magnetic moment "mu" of a closed circuit loop is a vector quantity, the product of its current and "area vector". One can express the torque on a loop as
```
             tau = mu x B
```

Viewgraph 1

Viewgraph 2

Viewgraph 3

Viewgraph 4

Viewgraph 5

Viewgraph 6

Viewgraph 7

Viewgraph 8

Viewgraph 9

Viewgraph 10

Viewgraph 11

Viewgraph 12

Viewgraph 13