 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Gauss' Law
This lecture is based on HRW, Sections 24.1-24.5
- Coulomb's Law provides one way to solve problems involving
electricity --- but it can sometimes require big, messy
integrals.
Gauss' Law provides a very different way to approach
certain types of problems; it can make the solution
much simpler to find.
- Electric flux through a surface is defined as the dot product
of the electric field and the "vector area" of the surface,
where the "vector area" points in the direction of the normal
to the surface
- Units of electric flux are N-m^2/C
- Flux going INTO a closed surface is negative;
flux coming OUT OF a closed surface is positive
- Gauss' Law states that the net electric flux through any closed
surface is equal to the electic charge enclosed by that surface,
divided by the permittivity of free space (epsilon-nought)
- Charges in a conductor arrange themselves so that
 Viewgraph 1
Viewgraph 1
 Viewgraph 2
Viewgraph 2
 Viewgraph 3
Viewgraph 3
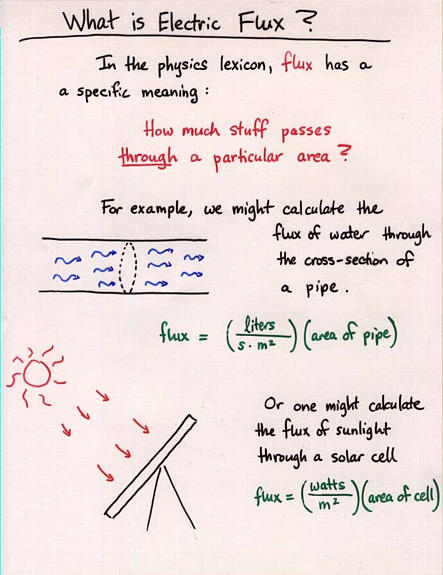 Viewgraph 4
Viewgraph 4
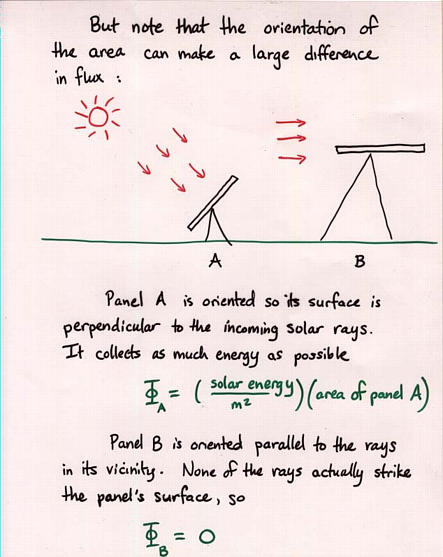 Viewgraph 5
Viewgraph 5
 Viewgraph 6
Viewgraph 6
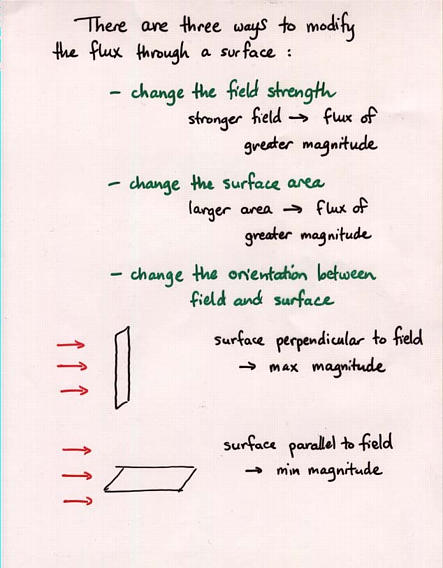 Viewgraph 7
Viewgraph 7
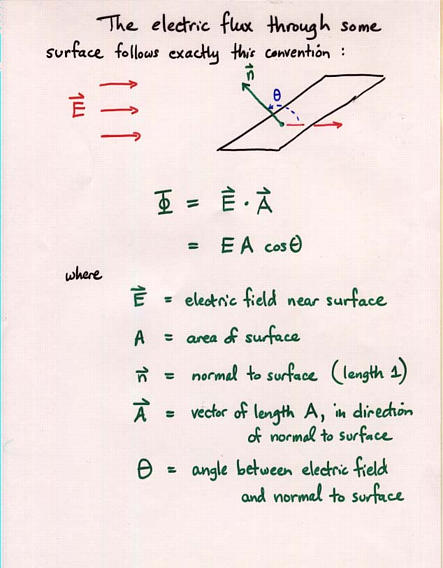 Viewgraph 8
Viewgraph 8
 Viewgraph 9
Viewgraph 9
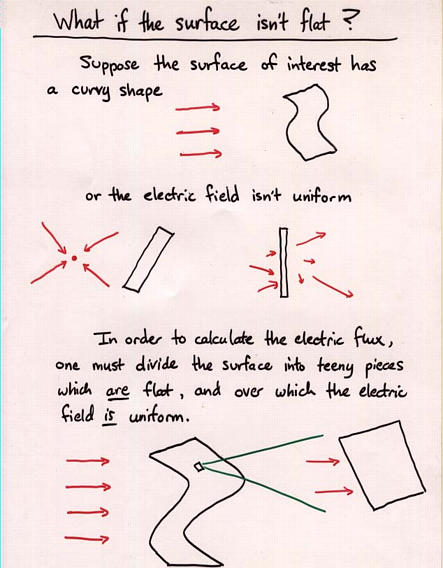 Viewgraph 10
Viewgraph 10
 Viewgraph 11
Viewgraph 11
 Viewgraph 12
Viewgraph 12
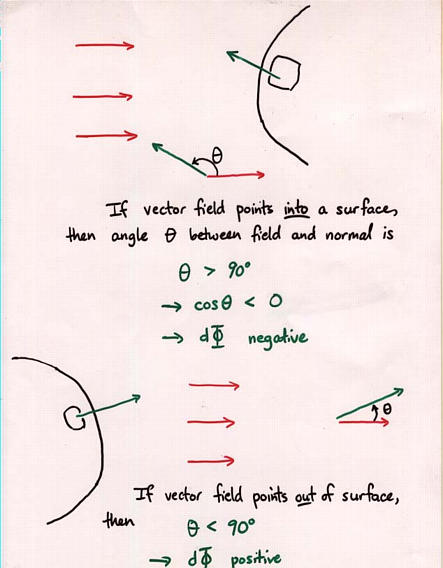 Viewgraph 13
Viewgraph 13
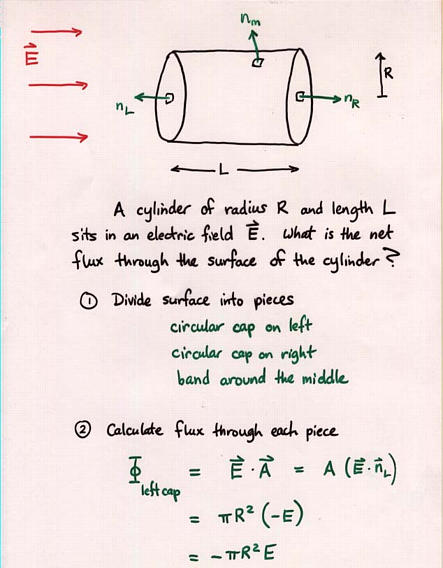 Viewgraph 14
Viewgraph 14
 Viewgraph 15
Viewgraph 15
 Viewgraph 16
Viewgraph 16
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
 Viewgraph 1
Viewgraph 1 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
 Viewgraph 1
Viewgraph 1 Viewgraph 2
Viewgraph 2 Viewgraph 3
Viewgraph 3 Viewgraph 4
Viewgraph 4 Viewgraph 5
Viewgraph 5 Viewgraph 6
Viewgraph 6 Viewgraph 7
Viewgraph 7 Viewgraph 8
Viewgraph 8 Viewgraph 9
Viewgraph 9 Viewgraph 10
Viewgraph 10 Viewgraph 11
Viewgraph 11 Viewgraph 12
Viewgraph 12 Viewgraph 13
Viewgraph 13 Viewgraph 14
Viewgraph 14 Viewgraph 15
Viewgraph 15 Viewgraph 16
Viewgraph 16 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.