 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Electric fields, Superposition,
Motion of charged particles in uniform electric field
This lecture is based on Serway, Sections 23.4 - 23.7.
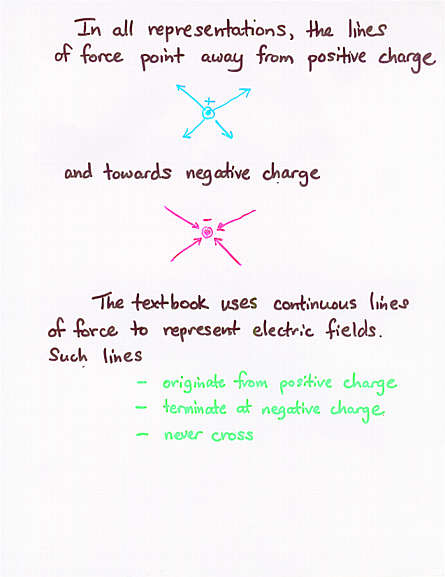
- One can represent the electric field by means of arrows, or by means
of continuous lines
- lines originate on positive charges
- lines terminate on negative charges
- lines never cross
- the density of lines indicates the strength of the electric field
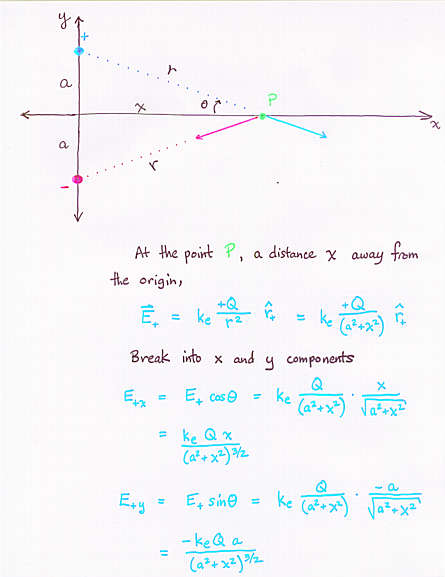
- The principle of superposition states that the electric field due
to a group of particles is simply the vector sum of the electric
field due to each particle considered individually
- The electric field of a dipole decreases with distance cubed (not squared)
- One can calculate the electric field due to a
continous distribution of charge
by integrating the contributions of each little bit of material
- When calculating electric fields,
- look for symmetry -- it can eliminate one component of the field
- figure out what the appropriate charge density is
- divide the object into little chunks
- figure out the charge density of each chunk (it may depend on position)
- calculate the electric field created by each chunk
- set up the integral, then integrate
- check the sign of the answer when finished
- look at the behavior of the field in limiting cases
(e.g. very far away); do they make sense?
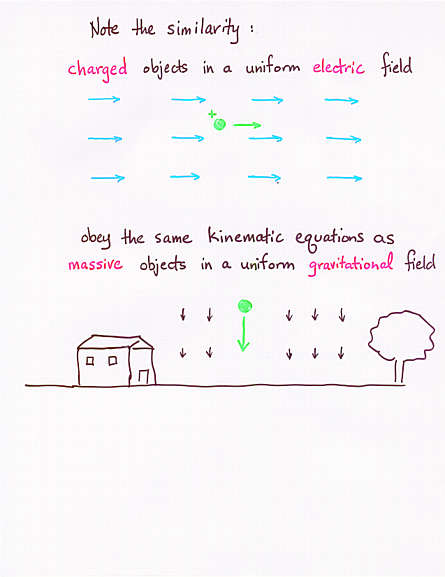
- a charged particle in a uniform electric field experiences a constant
acceleration -- like an object falling in a uniform gravitational field
- it obeys the same 1-D kinematic equations you learned in mechanics
 Viewgraph 1
Viewgraph 1
 Viewgraph 2
Viewgraph 2
 Viewgraph 3
Viewgraph 3
 Viewgraph 4
Viewgraph 4
 Viewgraph 5
Viewgraph 5
 Viewgraph 6
Viewgraph 6
 Viewgraph 7
Viewgraph 7
 Viewgraph 8
Viewgraph 8
 Viewgraph 9
Viewgraph 9
 Viewgraph 10
Viewgraph 10
 Viewgraph 11
Viewgraph 11
 Viewgraph 12
Viewgraph 12
 Viewgraph 13
Viewgraph 13
 Viewgraph 14
Viewgraph 14
 Viewgraph 15
Viewgraph 15
 Viewgraph 16
Viewgraph 16
 Viewgraph 17
Viewgraph 17
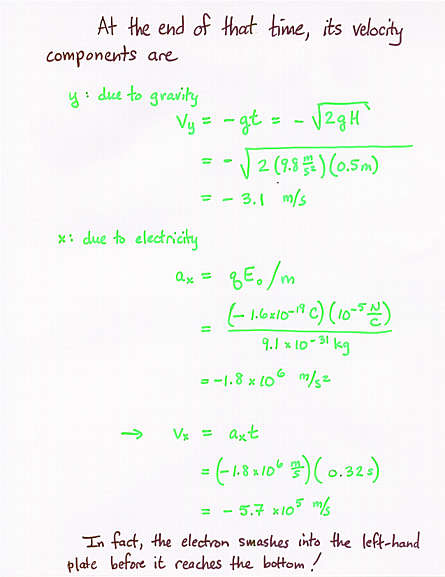 Viewgraph 18
Viewgraph 18
This is an example of calculating the electric field due to a disk
with varying charge; it's complicated, but shows the same steps
as the problems we did in class.
Appendix problem, viewgraph 1
Appendix problem, viewgraph 2
Appendix problem, viewgraph 3
Appendix problem, viewgraph 4
Appendix problem, viewgraph 5
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
 Viewgraph 1
Viewgraph 1 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
 Viewgraph 1
Viewgraph 1 Viewgraph 2
Viewgraph 2 Viewgraph 3
Viewgraph 3 Viewgraph 4
Viewgraph 4 Viewgraph 5
Viewgraph 5 Viewgraph 6
Viewgraph 6 Viewgraph 7
Viewgraph 7 Viewgraph 8
Viewgraph 8 Viewgraph 9
Viewgraph 9 Viewgraph 10
Viewgraph 10 Viewgraph 11
Viewgraph 11 Viewgraph 12
Viewgraph 12 Viewgraph 13
Viewgraph 13 Viewgraph 14
Viewgraph 14 Viewgraph 15
Viewgraph 15 Viewgraph 16
Viewgraph 16 Viewgraph 17
Viewgraph 17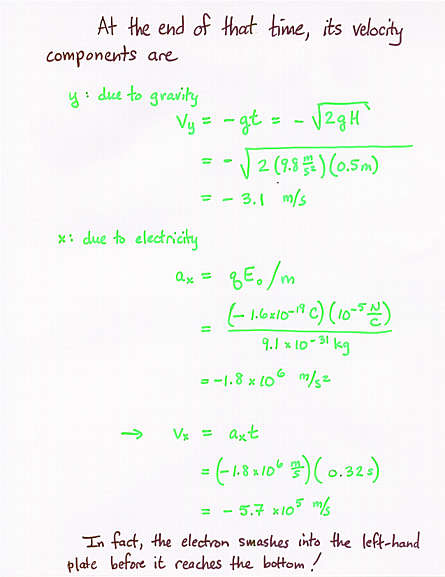 Viewgraph 18
Viewgraph 18 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.