 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Sources of Magnetic Field
This lecture is based on Serway, Sections 30.1 to 30.3.
It covers some ways in which one can calculate the magnetic field
created by a current running through a wire.
- There are many similarities between the electric and magnetic
fields -- you will see them here, and in future weeks.
- Magnetic fields can be created by current moving through a conductor.
- The Biot-Savart Law describes the magnetic field due to a tiny
section of current, at some distance away from the wire.
- One can integrate the Biot-Savart Law all the way across
a wire in order to calculate the total magnetic field it generates.
The integral may be complicated and difficult.
- In a few situations with strong symmetry, one can use Ampere's
Law to calculate the strength of a magnetic field created
by current running through a conductor.
- Ampere's Law relates the integral of magnetic field dotted with
displacement around a loop to the amount of current running
in wires which pass through the loop.
- Ampere's Law is an analog (in two dimensions) to Gauss' Law (in three
dimensions): both relate the properties of a field and a surface
(or loop) to the amount of stuff within the surface (or loop).
- One wire carrying a current creates a magnetic field; if there's
another wire carrying a current nearby, the magnetic field
will exert a force on it.
- If two wires carry current in the same direction, the magnetic force
pulls them together; if they carry current in opposite directions,
the magnetic force pushes them apart.
- The strength of the force between wires carrying current decreases
as the inverse distance between them.
 Viewgraph 1
Viewgraph 1
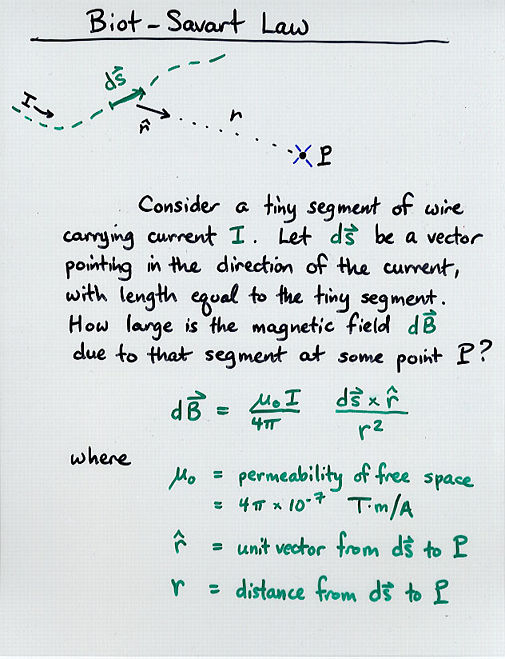 Viewgraph 2
Viewgraph 2
 Viewgraph 3
Viewgraph 3
 Viewgraph 4
Viewgraph 4
 Viewgraph 5
Viewgraph 5
 Viewgraph 6
Viewgraph 6
 Viewgraph 7
Viewgraph 7
 Viewgraph 8
Viewgraph 8
 Viewgraph 9
Viewgraph 9
 Viewgraph 10
Viewgraph 10
 Viewgraph 11
Viewgraph 11
 Viewgraph 12
Viewgraph 12
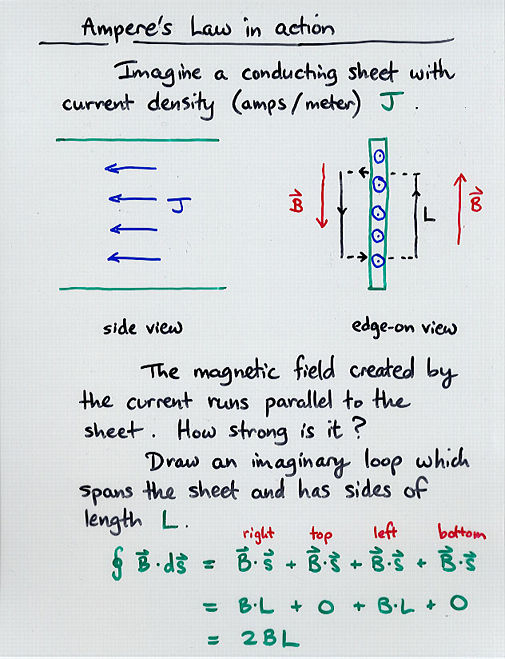 Viewgraph 13
Viewgraph 13
 Viewgraph 14
Viewgraph 14
 Viewgraph 15
Viewgraph 15
 Viewgraph 16
Viewgraph 16
 Viewgraph 17
Viewgraph 17
 Viewgraph 18
Viewgraph 18
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
 Viewgraph 1
Viewgraph 1 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
 Viewgraph 1
Viewgraph 1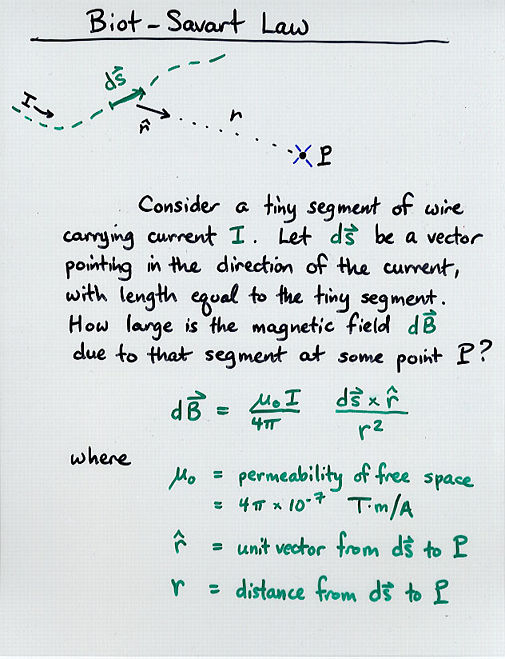 Viewgraph 2
Viewgraph 2 Viewgraph 3
Viewgraph 3 Viewgraph 4
Viewgraph 4 Viewgraph 5
Viewgraph 5 Viewgraph 6
Viewgraph 6 Viewgraph 7
Viewgraph 7 Viewgraph 8
Viewgraph 8 Viewgraph 9
Viewgraph 9 Viewgraph 10
Viewgraph 10 Viewgraph 11
Viewgraph 11 Viewgraph 12
Viewgraph 12 Viewgraph 13
Viewgraph 13 Viewgraph 14
Viewgraph 14 Viewgraph 15
Viewgraph 15 Viewgraph 16
Viewgraph 16 Viewgraph 17
Viewgraph 17 Viewgraph 18
Viewgraph 18 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.