 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
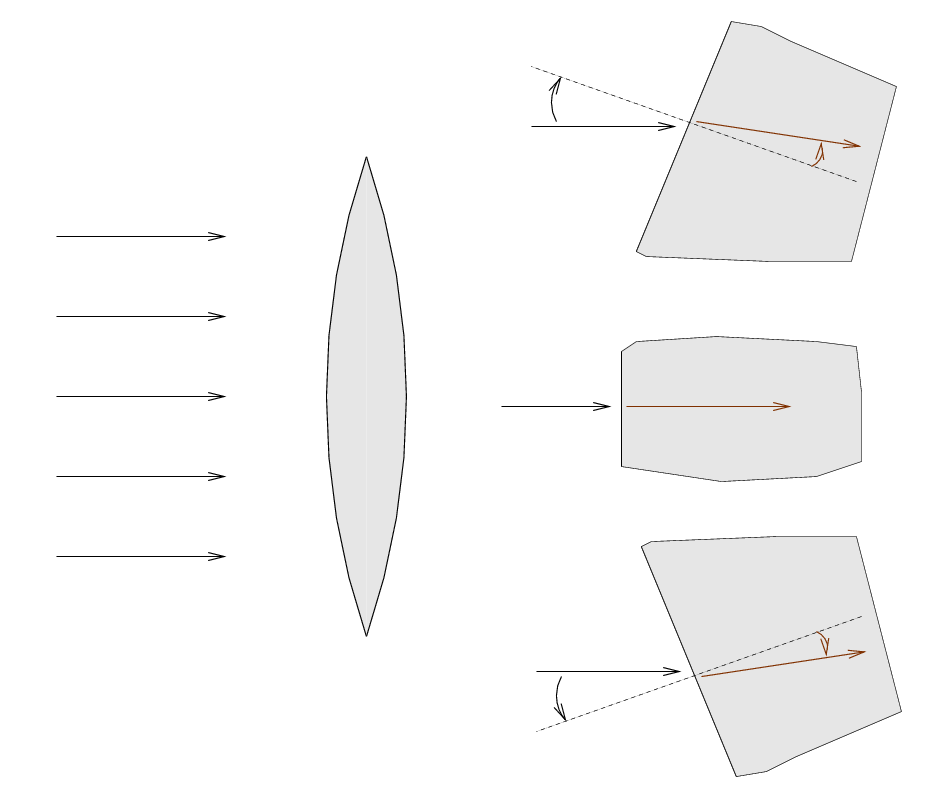
When light strikes a boundary bewteen two media, it can refract through the boundary, changing its direction. You can use Snell's Law to figure out the new direction taken by a light ray, if you know the incoming angle and the indices of refraction of the two materials.
If you take a piece of transparent glass or plastic, and grind it into a shape we call a thin lens, then the overall effect of the refraction of light passing through the material can be described in a relatively simple way.

If you analyze the refraction when the rays leave the lens and pass back into air, you'll see that -- because the lens curves in the opposite manner on its far side -- the rays are bent EVEN MORE in the same directions. The result is that, for a lens with just the right shape, all the light rays come together at a single point, which we call the focus of the lens.

Q: Will light of all wavelengths come to a focus
at the same point?
perhaps this will refresh your memory
For lenses with surfaces which are curved to follow spheres with radii r1 and r2, one can compute the location of this focal point using the Lens Maker's Equation

Note that the direction of the curvature matters: in the example above, the left side curves out to the left, while the right side curves out to the right. That means that if we call the radius r1 positive, then the radius r2 of the other side must be NEGATIVE. For a symmetric thin lens, like the one above, the focal length is simply

The focal length f has units of length: it's the distance from the lens to the focal point.
Now, if the incoming light rays are not parallel, things become more complicated. If we trace the path of rays from a real, physical object as they pass through a lens, we find that they (sometimes) form an image on the other side of the lens. We'll use this notation:
f = focal length of lens
o = distance from object to lens
i = distance from lens to image
positive if on side opposite to object
negative if on same side as object
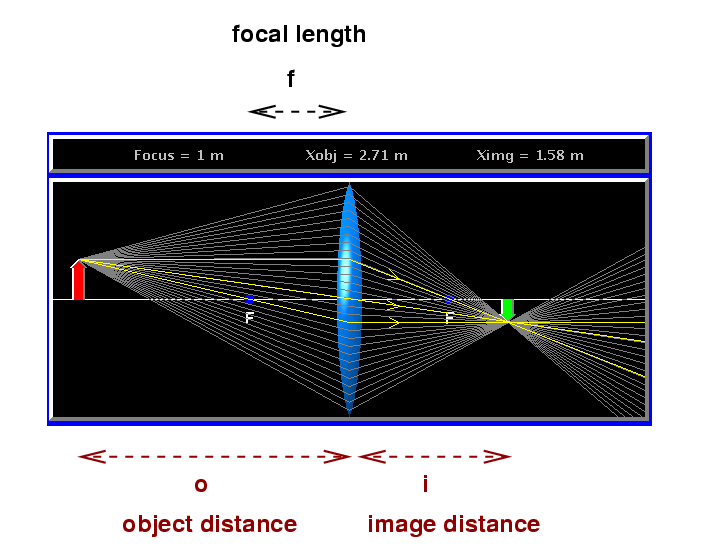
With this notation, there is a simple relationship between the three distances involved in forming an image:
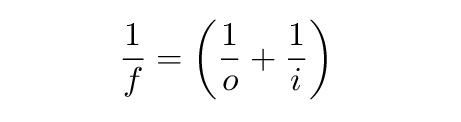
What's the difference between real and virtual images?
For example, consider a woman looking in a mirror, like this:

This woman sees an image of herself. Can she trace that image on a sheet of cardboard with a pencil?
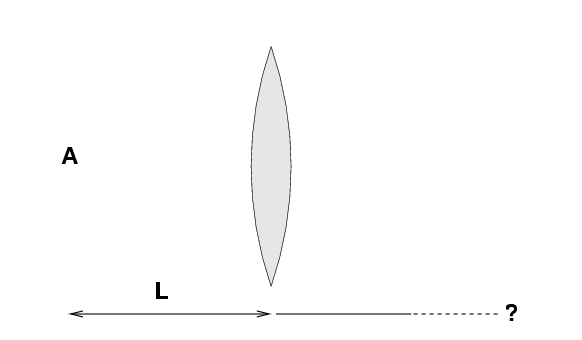
Optical Ollie has a thin lens of focal length f = 50 cm.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.