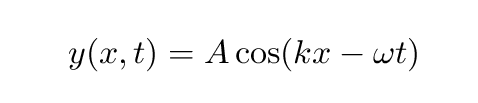
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Physicists like to use differential equations to describe physical phenomena: they are compact, provide some insight into the mathematical behavior, and they occasionally suggest connections between otherwise very different situations. Let's look at one very widely used differential equation.
Start with the equation of a wave travelling on a string:
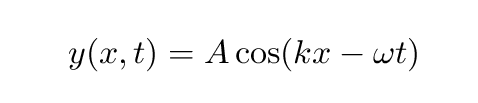
Let's take the partial derivative of this equation with respect to position x, and also the partial derivative with respect to time t.
Now repeat the procedure to find the second partial derivative with respect to each variable....
You should end up with
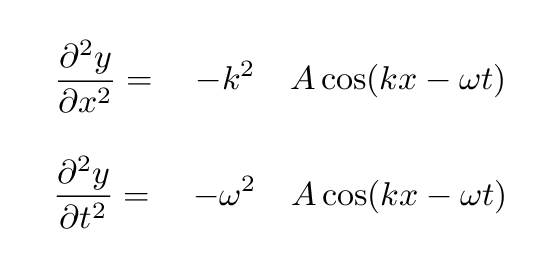
Hmmm. These are ALMOST the same. The only difference is the coefficient out front. I can make the spatial derivative equal to the time derivative if I multiply by the right ratio:

But this ratio of angular frequency to wave number can be expressed in terms of the speed of the wave.
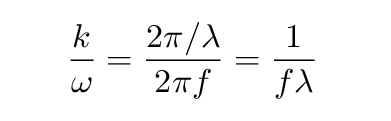
And that means that the (second) spatial derivative and the (second) time derivative are connected by the speed of the wave.
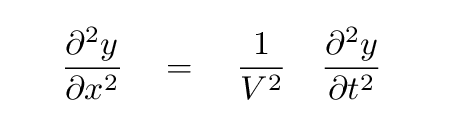
This relationship is known as the wave equation. In a few weeks, we are going to start studying the behavior of electromagnetic waves: disturbances in an electric field E(x, t) which obey
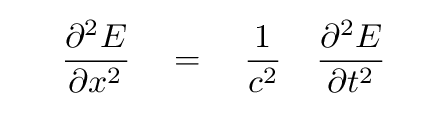
or, if we use a special symbol to denote a partial derivative in three-dimensional space,
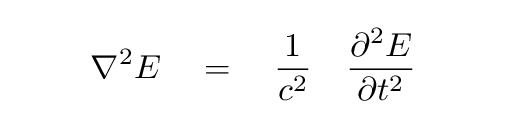
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.