-
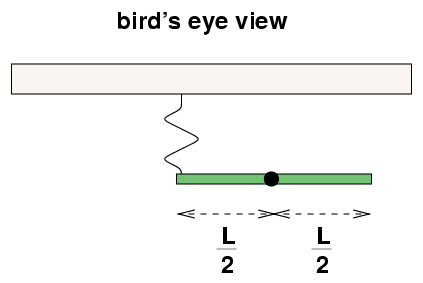
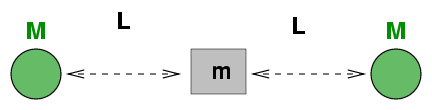
Fred places a green rod of mass m = 3 kg
and length L = 1.5 m
on the frictionless floor of his lab.
He drills a hole through the very center of the rod
and sticks a pin through the hole, so that the rod
is free to rotate around the pin.
He attaches one end of a spring to the left end of the rod,
and the other end of the spring to the wall.
Fred pulls the left end of the rod away from the wall
by a small distance, then releases it.
The rod rocks back and forth.
- Show that the motion is SHM.
- Fred measures 5 complete oscillations
in 20 seconds.
What is the force constant of the spring?
-
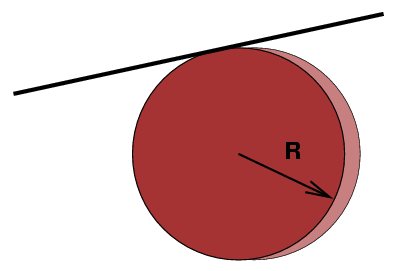
Fred glues the edge of a uniform disk of mass M
and radius R to a rod running just below his ceiling.
The disk can swing back and forth below the rod.
Fred pulls the disk to the side a small distance,
then releases it. It starts to swing back and forth.
- What is the period of the motion?
- Fred wants to make the period exactly 10 seconds.
Provide one combination of mass and radius that
will yield this period.
(Hint: Fred will need some very high ceilings ...)
-
Alice has a spring of force constant k = 200 N/m
and a block of mass m = 5 kg.
She wants to create an oscillation with a maximum
speed of v = 2.3 m/s,
so she pulls the block away from its rest position
with a force F, holds it for a moment,
then releases it.
- How much force F should Alice exert when pulling
the block away from its equilibrium position?
- How much work must Alice do to set
the block in motion as described?
-
I've made an equilateral triangle from 3 meter sticks
taped together.
I hang the triangle from one vertex and let it swing
back and forth.
- What is the moment of inertia of the triangle
around the pivot point?
- What is the period of oscillation?

-
I take a sheet of cardboard from the back of an ordinary
pad of letter-sized paper. I poke a hole in the cardboard,
4 inches above the center,
and suspend the cardboard by a pin through this hole.
I pull the left corner to the side a bit and release it.
It starts to swing back and forth.
- What is the period of the motion?
Warning: this is a tough one.
-
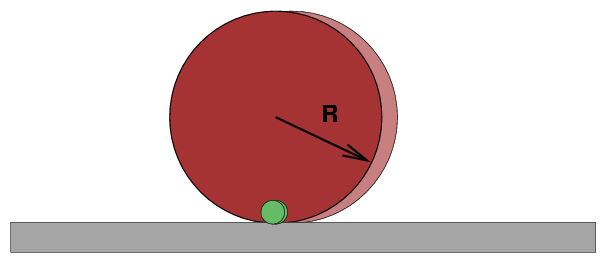
Jane has a big uniform disk of mass M = 50 kg
and radius R = 1 m.
She also has a tiny chunk of lead,
of mass m = 3 kg;
treat the chunk like a point-mass.
Jane glues the chunk of lead onto the big disk
so that it is at the outer edge.
Jane places her object onto the floor, so that
it balances vertically as shown above.
The little lead chunk is directly below the
center of the big disk. Everything is at rest.
Jane then rolls the object a small distance to the right,
holds it for a moment, then releases it.
It rolls back and starts to oscillate around the starting point.
- Is this SHM? Show why or why not.
- If it is, what is the period of the motion?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.


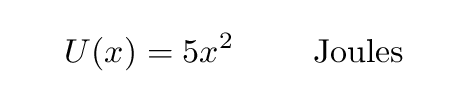
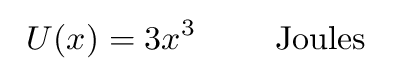
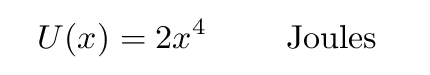




 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.