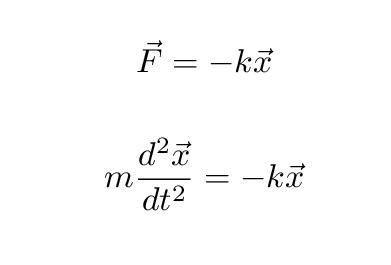
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The general problem of motion in a resistive medium is a tough one. We will make one assumption about the nature of the resistance which simplifies things considerably, and which isn't unreasonable in some common real-life situations.
Start with an ideal harmonic oscillator, in which there is no resistance at all:
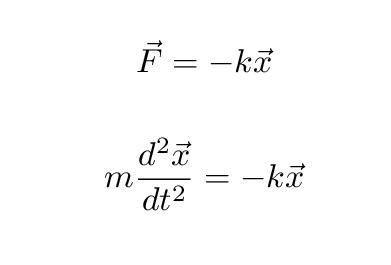
We could write the equation this way ...
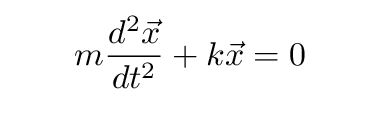
You know the solution to this equation, right?
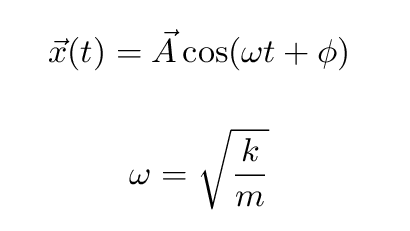
Okay, now let's add some resistance. We'll make the assumption that the resistive force
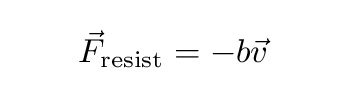
Is this always true? No. Is it sometimes true? Yes --- to some degree. For example, when objects move slowly through the air, at just a few meters per second, the force of air resistance grows roughly with speed in a linear fashion.
If we make this assumption, then the sum of forces on the object becomes
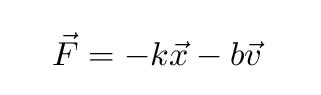
We can write everything in terms of position x(t) and its derivatives:
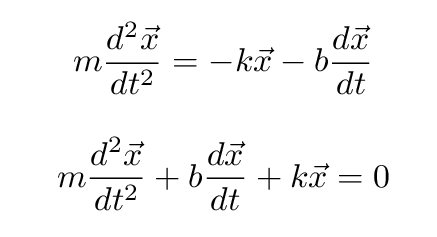
Uh-oh. This could be trouble. How can we solve this differential equation?
The answer is (in my case, at least), take a guess ... but make it an educated guess. I know that solutions to the simpler differential equation without the velocity term look like sines and cosines; and solutions to the simpler differential equation without the acceleration term look like exponential functions. So, I'm going to GUESS that the solution to this big differential equation will be some sort of combination of those two solutions. (I'm going to drop the vector notation at this point, because we're going to have enough to deal with as it is ...) So we GUESS

Okay, your turn. Please write down the first derivative of this function. Then write down the second derivative of this function. It may take a while -- that's okay.
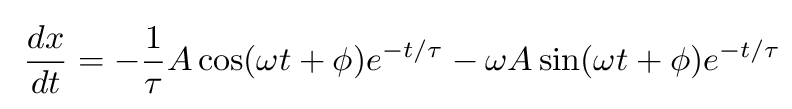
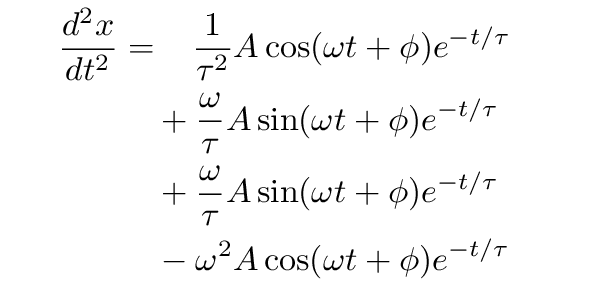
Phew.
Now, go back to the equation of motion for the object:
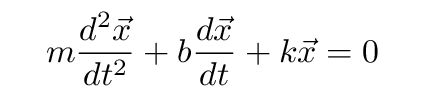
In order to verify that our GUESSED solution actually does satisfy this equation, we need to insert the full expressions for the original function, its first derivative, and its second derivative ... and then make sure that it all adds up to zero. Let's do that ...
much pain and agony later ....
Yes, our guessed solution will satisfy the equation as long as
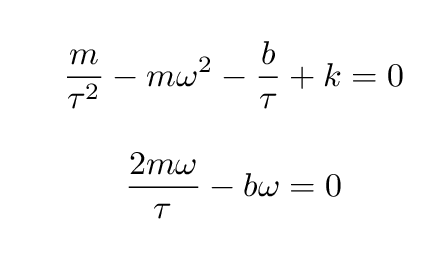
So, if we can measure the mass m, and the force constant k, and the resistance force coefficient b, then we can compute
Please solve for tau and omega in terms of the other variables now.
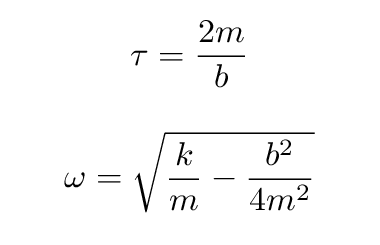
Well, fine, we have solved some equations. But what do they MEAN?
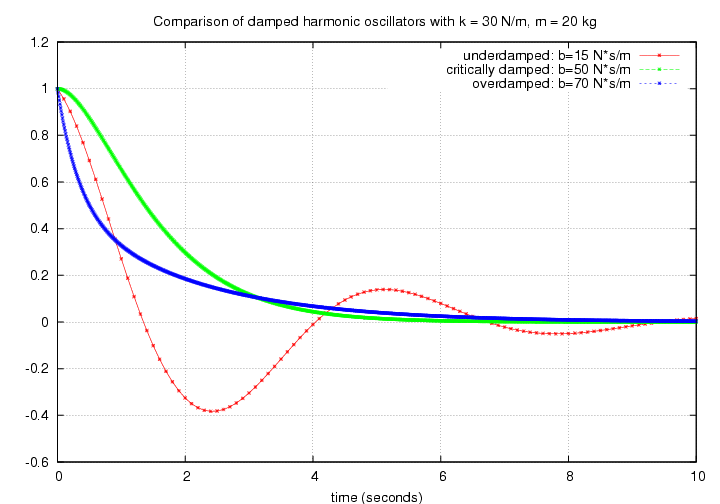
The ordinary harmonic oscillator moves back and forth forever. It converts kinetic to potential energy, but conserves total energy perfectly. It will never stop.

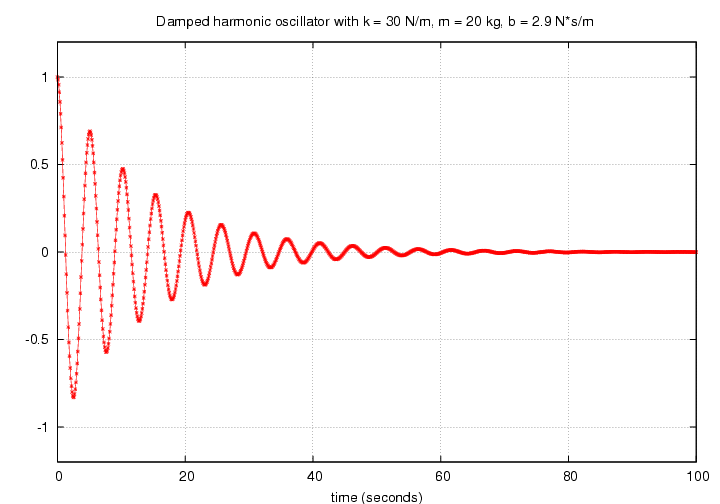
A lightly damped harmonic oscillator moves with ALMOST the same frequency, but it loses amplitude and velocity and energy as times goes on. The timescale over which the amplitude decays is related to the time constant tau .

As the resistive force increases (b increases), the decay happens more quickly.
When the combination of parameters is just right, critically-damped so that
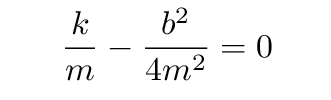
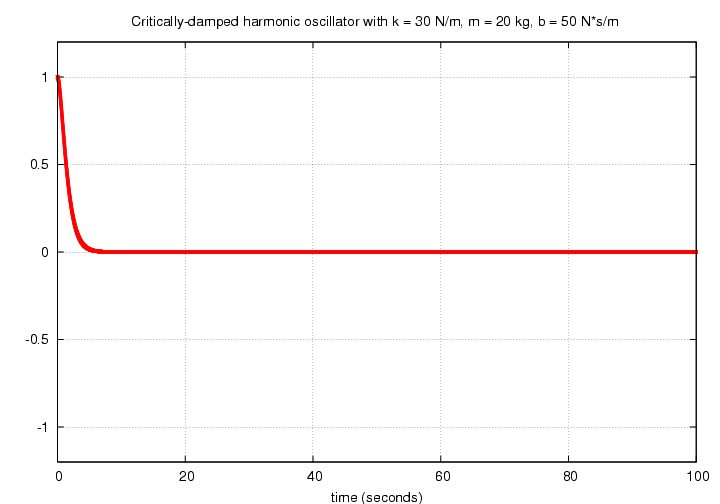
then the oscillator never really oscillates: it decays exponentially, just barely not reaching the other side of the equilibrium.
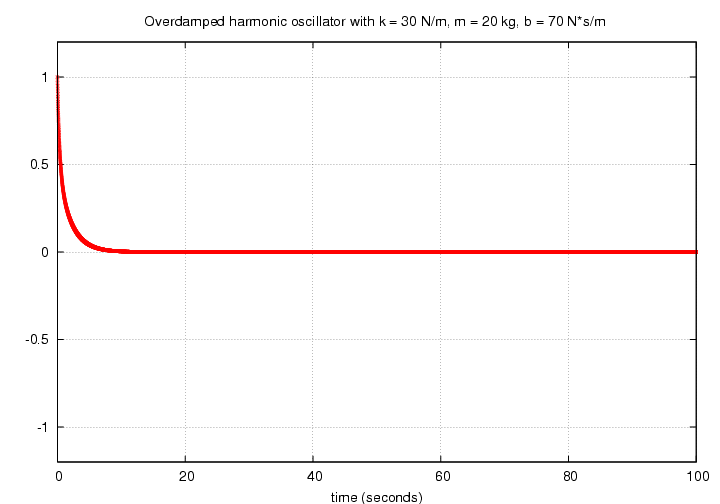
If one makes the resistive force even stronger, the over-damped oscillator decays in an even quicker manner.
Let's look at the first few seconds of an under-damped, critically-damped, and over-damped case so that we can see the initial motions more clearly.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.